2025 AMC 8
Complete problem set with solutions and individual problem pages
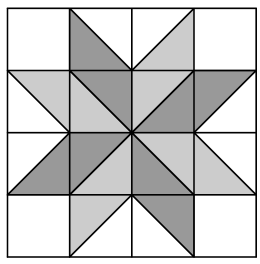
The eight-pointed star, shown in the figure below, is a popular quilting pattern. What percent of the entire grid is covered by the star?
- A.
- B.
- C.
- D.
- E.
Solution 1
Each of the unshaded triangles has base length and height , so they all have area . Each of the unshaded unit squares has area . The area of the shaded region is equal to the area of the entire grid minus the area of the unshaded region, or . The star is then , or percent of the entire grid.
Solution 2
There are total squares in the diagram and each square has triangles whose areas are half the area of a unit square. Thus, the total number of triangles in the diagram is triangles. There are shaded triangles in the diagram, so the area of the star is , or percent.
The table below shows the ancient Egyptian hieroglyphs that were used to represent different numbers.
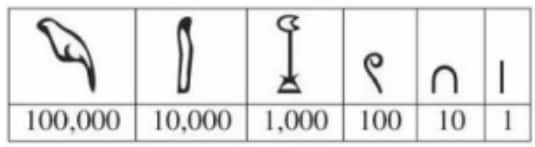
For example, the number was represented by the hieroglyphs . What number is represented by the following combination of hieroglyphs?
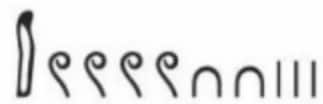
- A.
- B.
- C.
- D.
- E.
Solution 1
The first hieroglyph is worth , the next 4 are worth , the next are worth , and the last are worth . Therefore, the answer is
Solution 2
Simply notice that the first hieroglyph represents , and the next ones represent hundreds. The only answer choice with a in the thousands place and a in the hundreds place is answer choice
Buffalo Shuffle-o is a card game in which all the cards are distributed evenly among all players at the start of the game. When Annika and of her friends play Buffalo Shuffle-o, each player is dealt cards. Suppose more friends join the next game. How many cards will be dealt to each player?
- A.
- B.
- C.
- D.
- E.
We start with Annika and of her friends playing, meaning that there are players. This must mean that there is a total of cards. If more players joined, there would be players, and since the cards need to be split evenly, this would mean that each player gets Buffalo Shuffle-O cards each meaning that the final answer is 10.
Lucius is counting backward by s. His first three numbers are , , and . What is his th number?
- A.
- B.
- C.
- D.
- E.
Solution 1
We plug and into the formula for the th term of an arithmetic sequence whose first term is and common difference is to get .
Solution 2
Since we want to find the th number Lucius says after he says , is subtracted from his number times, so our answer is
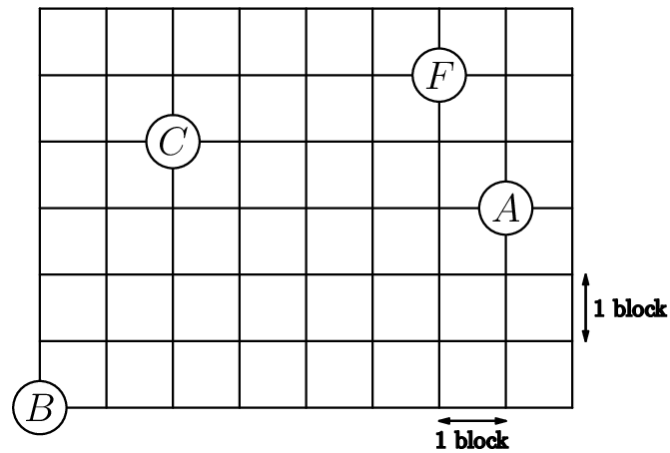
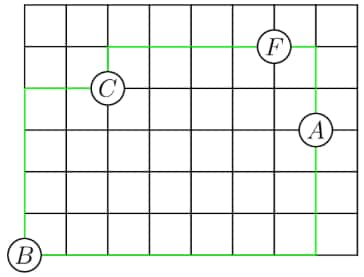
Betty drives a truck to deliver packages in a neighborhood whose street map is shown below. Betty starts at the factory (labeled ) and drives to location , then , then , before returning to . What is the shortest distance, in blocks, she can drive to complete the route?
- A.
- B.
- C.
- D.
- E.
Solution 1
Each shortest possible path from to follows the edges of the rectangle. The following path outlines a path of units:
Solution 2
We can find the shortest distance using a line diagonally from one point to the other, creating a sort of slope, then find the sum of rise and run of the slope, which happens to be the shortest distance, repeat this process until you get back to Point , and you should get , which is equal to .
Sekou writes the numbers After he erases one of his numbers, the sum of the remaining four numbers is a multiple of Which number did he erase?
- A.
- B.
- C.
- D.
- E.
Solution 1
The sum of all five numbers is . Since is more than a multiple of , the number being subtracted must be more than a multiple of . Thus, the answer is .
Solution 2
The sum of the residues of these numbers modulo is . Hence, the number being subtracted must be congruent to modulo . The only such answer is .
On the most recent exam on Prof. Xochi's class,
students earned a score of at least ,
students earned a score of at least ,
students earned a score of at least ,
students earned a score of at least ,
How many students earned a score of at least and less than ?
- A.
- B.
- C.
- D.
- E.
Solution 1
people scored at least , and out of these people, of them earned a score that was not less than , so the number of people that scored in between at least and less than is .
Solution 2
Let denote the number of people who had a score of at least , but less than , and let denote the number of people who had a score of at least but less than . Our answer is equal to . We find , while . Thus, the answer is .
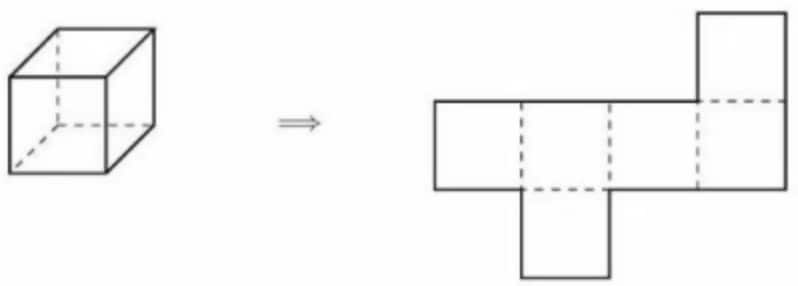
Isaiah cuts open a cardboard cube along some of its edges to form the flat shape shown on the right, which has an area of square centimeters. What is the volume of the cube in cubic centimeters?
- A.
- B.
- C.
- D.
- E.
Solution 1
Each of the faces of the cube have equal area, so the area of each face is equal to , making the side length . From this, we can see that the volume of the cube is
Solution 2
Let the side length of the cube shown be equal to centimeters. The surface area of this cube is equal to the area of the net of the cube, which is equal to square centimeters. The surface area of this cube is also square centimeters, so we have
However, we aren't done. We have found that the side length of the cube is , but the question asks for the volume of the cube, which is equal to cubic centimeters.
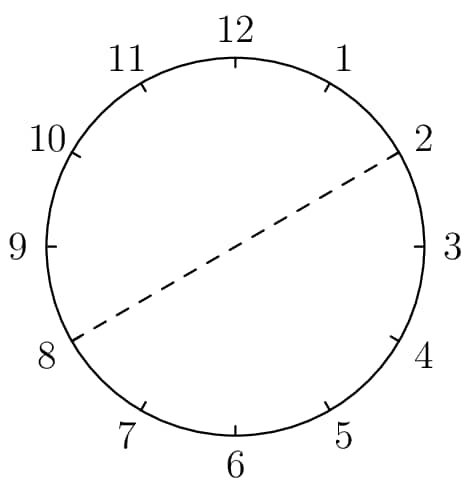
Ningli looks at the pairs of numbers directly across from each other on a clock. She takes the average of each pair of numbers. What is the average of the resulting numbers?
- A.
- B.
- C.
- D.
- E.
Solution 1
Our answer is
Solution 2
We proceed with brute force. All of the pairs of opposite numbers on the clock are , , , , , , where order doesn't matter. The averages of each of these pairs are and respectively, and the average these numbers is
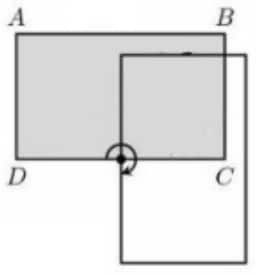
In the figure below, is a rectangle with sides of length inches and = 3 inches. Rectangle is rotated clockwise around the midpoint of side to give a second rectangle. What is the total area, in square inches, covered by the two overlapping rectangles?
- A.
- B.
- C.
- D.
- E.
The area of each rectangle is . Then the sum of the areas of the two regions is the sum of the areas of the two rectangles, minus the area of their overlap. To find the area of the overlap, we note that the region of overlap is a square, each of whose sides have length (as they are formed by the midpoint of one of the long sides and a vertex). Then the answer is .
A consists of four squares connected along their edges. There
are five possible tetromino shapes, , , , , and , shown below, which can be rotated or flipped over. Three tetrominoes are used to completely cover a rectangle. At least one of the tiles is an tile. What are the other two tiles?

- A.
and
- B.
and
- C.
and
- D.
and
- E.
and
The rectangle allows for possible places to put the S piece, with each possible placement having an inverted version. One of the cases looks like this:
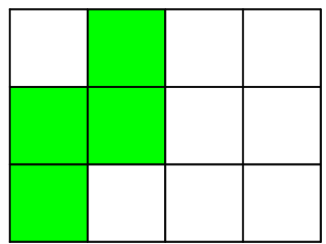
As you can see, there is a hole in the top left corner of the board, which would be impossible to fill using the tetrominos. There are three cases in which a hole isn't created; the S lies flat in the bottom left corner, it lies flat in the top right corner, or it stands upright in the center. All three tilings are shown below.
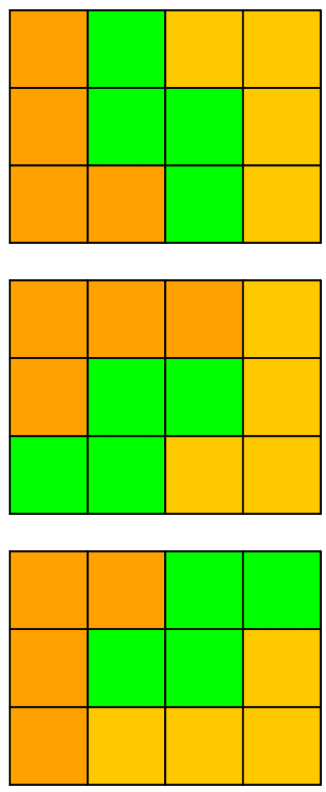
For each of the inverted cases, the L pieces can be inverted along with the S piece. Because the only cases that fill the rectangle after the S is placed are the ones that use two L pieces, the answer must be .
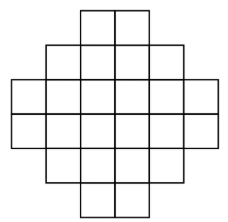
The region shown below consists of 24 squares, each with side length 1 centimeter. What is the area, in square centimeters, of the largest circle that can fit inside the region, possibly touching the boundaries?
- A.
- B.
- C.
- D.
- E.
Solution 1
The largest circle that can fit inside the figure has its center in the middle of the figure and will be tangent to the figure in points. By the Pythagorean Theorem, the distance from the center to one of these points is , so the area of this circle is .
Solution 2
Draw the circle in the grid and analyze the radius. Its radius is a little more than 2 but a lot less than 2.5, so the area is a little more than . So, the area of the circle is with a radius of approximately 2.23.
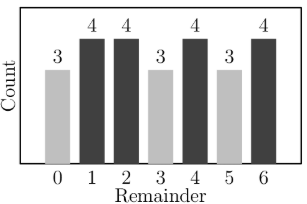
Each of the even numbers is divided by . The remainders are recorded. Which histogram displays the number of times each remainder occurs?
- A.
- B.

- C.

- D.
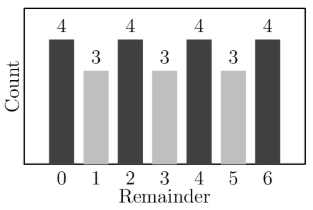
- E.

Solution 1
Let's take the numbers 2 through 14 (evens). The remainders will be 2, 4, 6, 1, 3, 5, and 0. This sequence keeps repeating itself over and over. We can take floor(50/14) = 3, so after the number 42, every remainder has been achieved 3 times. However, since 44, 46, 48, and 50 are left, the remainders of those will be 2, 4, 6, and 1 respectively. The only histogram in which those 4 numbers are set at 4 is histogram .
Solution 2
Writing down all the remainders gives us
In this list, there are numbers with remainder , numbers with remainder , numbers with remainder , numbers with remainder , numbers with remainder , numbers with remainder , and numbers with remainder . Manually computation of every single term can be avoided by recognizing the pattern alternates from to and there are terms. The only histogram that matches this is .
A number is inserted into the list , , , , . The mean is now twice as great as the median. What is ?
- A.
- B.
- C.
- D.
- E.
Solution 1
The median of the list is , so the mean of the new list will be . Since there are numbers in the new list, the sum of the numbers will be . Therefore,
Solution 2
Since the average right now is 10, and the median is 7, we see that N must be larger than 10, which means that the median of the 6 resulting numbers should be 7, making the mean of these 14. We can do 2 + 6 + 7 + 7 + 28 + N = 14 * 6 = 84. 50 + N = 84, so N =
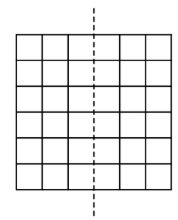
Kei draws a -by- grid. He colors of the unit squares silver and the remaining squares gold. Kei then folds the grid in half vertically, forming pairs of overlapping unit squares. Let and equal the least and greatest possible number of gold-on-gold pairs, respectively. What is the value of ?
- A.
- B.
- C.
- D.
- E.
Solution 1
First, we note that there are "pairs" of squares folded on top of each other after the folding. The minimum number of gold pairs occurs when silver squares occupy the maximum number of pairs, and the maximum number of gold pairs occurs when silver squares occupy the minimum number of pairs. The latter case occurs when all silver squares are placed in different pairs, resulting in gold pairs. The former case occurs when the silver squares are paired up as much as possible, resulting in complete pairs and another square occupying another pair slot. Then there are gold pairs. Our answer is .
Solution 2
We can see that the least number of gold-on-gold pairs will be obtained when the silver squares are placed on the two sides so that they don't overlap when folded over (because then it will minimize the number of gold-on-golds). We can see that if we split them up and on both sides, and then fold it, the number of gold-on-golds will be .
The maximum number of gold-on-golds will be achieved when the silver squares overlap when folded over, which will increase the number of gold-on-golds. If we align 6 silver squares with each other on each side, and put the last one somewhere else, we get the maximum is . Therefore, the answer is .
Five distinct integers from to are chosen, and five distinct integers from to are chosen. No two numbers differ by exactly . What is the sum of the ten chosen numbers?
- A.
- B.
- C.
- D.
- E.
Solution 1
Note that for no two numbers to differ by , every number chosen must have a different units digit. To make computations easier, we can choose from the first group and from the second group. Then the sum evaluates to .
Solution 2
For , we can add the first term and the last term, which is . If we add the second term and the second-to-last term it is also . There are pairs that sum to , so the answer is which equals .
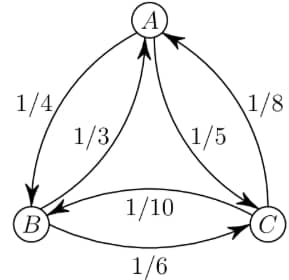
In the land of Markovia, there are three cities: , , and . There are 100 people who live in , 120 who live in , and 160 who live in . Everyone works in one of the three cities, and a person may work in the same city where they live. In the figure below, an arrow pointing from one city to another is labeled with the fraction of people living in the first city who work in the second city. (For example, of the people who live in work in .) How many people work in ?
- A.
- B.
- C.
- D.
- E.
Solution 1
There are people who do not work in city that live in city , meaning that people who live in city work in city . There are people who live in city and work in , as well as people who live in city that work in city . Therefore, the answer is .
Solution 2
We could also make an equation. Let's denote the number of people that live in city as , as , and as . If denotes the number of people working in city , then . This is because of the people from City and of the people from City work in city as shown in the image. We also know that of the people living in work in other cities. We are already given the values of variables , , and as , , and respectively. Plug the values it into the main equation like this: . We solve for it and get our answer .
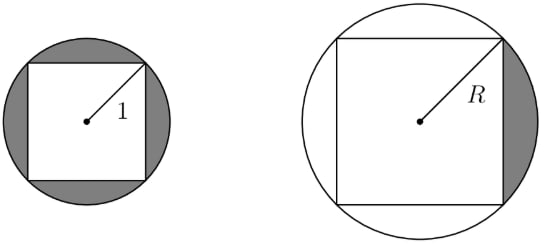
The circle shown below on the left has a radius of 1 unit. The region between the circle and the inscribed square is shaded. In the circle shown on the right, one quarter of the region between the circle and the inscribed square is shaded. The shaded regions in the two circles have the same area. What is the radius , in units, of the circle on the right?
- A.
- B.
- C.
- D.
- E.
Solution 1
The area of the shaded region in the circle on the left is the area of the circle minus the area of the square, or . The shaded area in the circle on the right is of the area of the circle minus the area of the square, or , which can be factored as . Since the shaded areas are equal to each other, we have , which simplifies to . Taking the square root, we have
Solution 2
We start with the first area. Since the square is inscribed, its diagonal is its side length is its area is , therefore the first area is . The second area is , found in a similar manner. Writing and solving the equation, we haveThe answer is .
Two towns, and , are connected by a straight road, miles long. Traveling from town to town , the speed limit changes every miles: from to to miles per hour (mph). Two cars, one at town and one at town , start moving toward each other at the same time. They drive at exactly the speed limit in each portion of the road. How far from town , in miles, will the two cars meet?

- A.
- B.
- C.
- D.
- E.
Solution 1
The first car, moving from town at miles per hour, takes minutes. The second car, traveling another miles from town , takes minutes. The first car has traveled for 3 minutes or th of an hour at miles per hour when the second car has traveled 5 miles. The first car has traveled miles from the previous miles it traveled at miles per hour. They have miles left, and they travel at the same speed, so they meet miles through, so they are miles from town .
Solution 2
From the answer choices, the cars will meet somewhere along the mph stretch. Car travels mph for miles, so we can use dimensional analysis to see that it will be of an hour for this portion. Similarly, car spends of an hour on the mph portion.
Suppose that car travels miles along the mph portion-- then car travels miles along the mph portion. By identical methods, car travels for hours, and car travels for hours.
At their meeting point, cars and will have traveled for the same amount of time, so we have
so , and miles. This means that car will have traveled miles.
Sarika, Dev, and Rajiv are sharing a large block of cheese. They take turns cutting off half of what remains and eating it: first Sarika eats half of the cheese, then Dev eats half of the remaining half, then Rajiv eats half of what remains, then back to Sarika, and so on. They stop when the cheese is too small to see. About what fraction of the original block of cheese does Sarika eat in total?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let the total amount of cheese be . We will track the amount of cheese Sarika eats throughout the process.
First Round: Sarika eats half of the total cheese, so she eats:
Second Round: Dev eats half of what remains after Sarika's turn, which is:
Third Round: Rajiv eats half of the remaining cheese after Dev's turn, which is:
At the end of the first round, the total cheese eaten is:
We observe that Sarika's consumption follows a geometric sequence. In the first round, she eats , and in subsequent rounds, she eats half of what remains from the previous round. This gives the following series for Sarika;s total consumption:
This is a geometric series with first term and common ratio . The sum of this infinite geometric series is given by the formula:
where is the first term and is the common ratio. Substituting and :
Thus, Sarika eats of the original block of cheese. The correct answer is:
Solution 2
Sarika eats of the original cheese, and then because the others eat and , she eats next, and then , and then so on. Since the values later are going to be too small to make a huge difference, we can use these values. She ate . We can replace the with a for now, so , which simplifies to around . Since there is a little bit more of the cheese to be accounted for, the amount that she eats will be around .
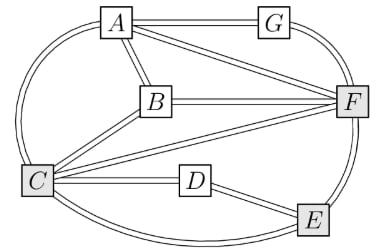
The Konigsberg School has assigned grades 1 through 7 to pods through , one grade per pod. Some of the pods are connected by walkways, as shown in the figure below. The school noticed that each pair of connected pods has been assigned grades differing by 2 or more grade levels. (For example, grades 1 and 2 will not be in pods directly connected by a walkway.) What is the sum of the grade levels assigned to pods , and ?
- A.
- B.
- C.
- D.
- E.
Solution 1
The key observation for this solution is to observe that pods and both have degree 5; that is, they are connected to five other pods. This implies that and must contain grades 1 and 7 in either order (if or contained any of grades 2, 3, 4, 5, or 6, then there would only be four possible grades for five pods, a contradiction). It does not matter which grade and gets (see Solution 2 below), so we will assume that pod is assigned grade 1, and pod is assigned grade 7.
Next, pod is the only pod which is not adjacent to pod , so pod must be assigned grade 6. Similarly, pod must be assigned grade 2.
Lastly, we need to assign grades 3, 4, and 5 to pods , , and . Note that and are adjacent; therefore, pods and must contain grades 3 and 5. We conclude that must be assigned grade 4. The requested sum is .
Solution 2
Suppose that we replaced each label with . That is, we replaced the grade assigned to with the grade , the grade assigned to with , and so on. We claim that if the initial labeling is valid (i.e., each pair of connected pods has grades differing by 2 or more), then so will the new labeling. This follows as if , then . This shows that if there is an assignment of grades to the pods, where , then there is a second, valid assignment.
But because this is an AMC 8 problem and there is only one correct answer, we can conclude that . Simplifying and solving for gives .
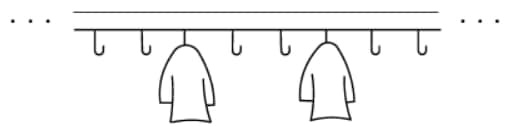
A classroom has a row of 35 coat hooks. Paulina likes coats to be equally spaced, so that there is the same number of empty hooks before the first coat, after the last coat, and between every coat and the next one. Suppose there is at least 1 coat and at least 1 empty hook. How many different numbers of coats can satisfy Paulina's pattern?
- A.
- B.
- C.
- D.
- E.
Solution 1
Suppose there are coats on the rack. Notice that there are "gaps" formed by these coats, each of which must have the same number of empty spaces (say, ). Then the values and must satisfy . We now use Simon's Favorite Factoring Trick as follows:
Our only restrictions now are that and . Other than that, each factor pair of produces a valid solution , which in turn uniquely determines an arrangement. Since has factors, our answer is .
Solution 2
Say Paulina placed coats. That will divide the 35 hooks into spaces and empty hooks. Therefore,The values of that satisfy this areThe answer is .
How many four-digit numbers have all three of the following properties?
(I) The tens and ones digit are both 9.
(II) The number is 1 less than a perfect square.
(III) The number is the product of exactly two prime numbers.
- A.
- B.
- C.
- D.
- E.
The Condition (II) perfect square must end in "" because Condition (I). Four-digit perfect squares ending in "" are .
Condition (II) also says the number is in the form . By the Difference of Squares, . Hence:
-
-
-
-
-
-
On this list, the only number that is the product of prime numbers (condition ) is , so the answer is .
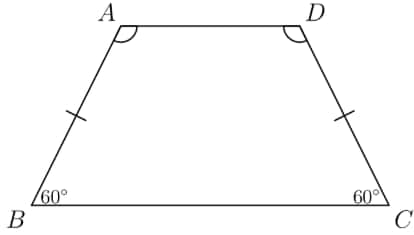
In trapezoid , angles and measure and . The side lengths are all positive integers, and the perimeter of is 30 units. How many non-congruent trapezoids satisfy all of these conditions?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let be the length of the shorter base, and let be the length of the longer one. Note that these two parameters, along with the angle measures and the fact that the trapezoid is isosceles, uniquely determine a trapezoid. We drop perpendiculars down from the endpoints of the top base. Then the length from the foot of this perpendicular to either vertex will be half the difference between the lengths of the two bases, or . Now, since we have a 30-60-90 triangle and this side length corresponds to the "30" part, the length of the hypotenuse (one of the legs) is . Then the perimeter of the trapezoid is . The only other stipulation for this trapezoid to be valid is that (which was our assumption). We can now easily count the valid pairs , yielding . It is clear that proceeding further would cause , so we have valid trapezoids.
Solution 2
Let be the length of and , and let be the length of the shorter base. Because and , the length of the longer base is . Therefore, the perimeter is . The number of positive integer pairs is , meaning the answer is .
way where you don't have to test pairs:
We can rearrange to . We want to be a positive integer so b is a positive integer. 30 is a multiple of 3 and is just subtracting multiples of 3's from 30 so every number on the numerator of is a multiple of 3 under 30 ( is also a positive integer so it can't be larger than 30 or not be a multiple of 3). For to be divisible by 2 it must be even, so we are finding even multiples of 3 under 30 which are 24, 18, 12, and 6. Each number will give us a valid and a valid pair giving us 4 solutions.
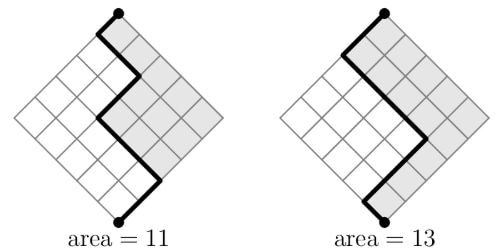
Makayla finds all the possible ways to draw a path in a diamond-shaped grid. Each path starts at the bottom of the grid and ends at the top, always moving one unit northeast or northwest. She computes the area of the region between each path and the right side of the grid. Two examples are shown in the figures below. What is the sum of the areas determined by all possible paths?
- A.
- B.
- C.
- D.
- E.
Solution 1
Step 1: To find the total number of paths, observe that all paths will have total steps. We have to choose which of these steps will be NE (the rest will be NW). So the total number of paths is . The formula for combinations is: and .
Step 2: Each path splits the total area of in two parts. So, for any path that gives area = , you can find a unique "sister" path that has an area = (in other words, the pair of paths have a combined area of 25). Possible ways to define the "sister" path are:
- Rotate the entire grid

- Swap each step of the original paths (for example, each NW becomes NE) (this is a reflection over the diagonal)
Step 3: There are a few ways to get from this observation to the total area:
- There are pairs of such paths, and the total area of each pair is . So the total area given by all paths is .
- Each of the paths gives an area of if you also count the "sister" paths. Since each "sister" path is also one of the , you have to divide by to avoid double counting. So the total area given by all paths is .
- Note that the average area of two "sister" paths is , so you can think about every path having this area on average. So the total area given by all paths is . The final answer is
Solution 2
If we test this problem on a smaller diamond, we have ways to go from to , and the total area is , so the average area is , which is also the area of the diamond divided by 2. If we assume this is true for a diamond, then the average area is . The number of paths from to is , and .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
