2023 AMC 8
Complete problem set with solutions and individual problem pages
What is the value of ?
- A.
- B.
- C.
- D.
- E.
Solution 1
By the order of operations, we have
Solution 2
We can simplify the expression above in another way:
A square piece of paper is folded twice into four equal quarters, as shown below, then cut along the dashed line. When unfolded, the paper will match which of the following figures?
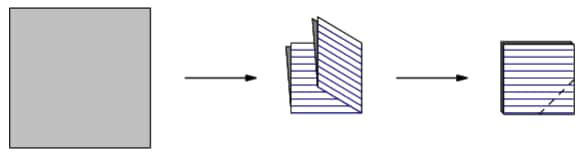
- A.

- B.

- C.

- D.
- E.
Solution 1
Notice that when we unfold the paper along the vertical fold line, we get the following shape:
It is clear that the answer is .
Solution 2
When you fold the paper in that specific way, it shows the top left square. That means that any cut you make on that folded part will look like that on that top left square. Since it is folded into four parts, the cut will reflect on all of the other 3 parts. Since there is a cut diagonally on the bottom right of that square, that will reflect on the other squares, making the shape of
Wind chill is a measure of how cold people feel when exposed to wind outside. A good estimate for wind chill can be found using this calculation
where temperature is measured in degrees Fahrenheit and the wind speed is measured in miles per hour (mph). Suppose the air temperature is and the wind speed is mph. Which of the following is closest to the approximate wind chill?
- A.
- B.
- C.
- D.
- E.
Solution 1
By substitution, we have
Solution 2 (Estimation)
is very close to - therefore, we can substitute into the equation to get
As is slightly less than , the correct answer is slightly less than . Therefore, the answer is .
The numbers from to are arranged in a spiral pattern on a square grid, beginning at the center. The first few numbers have been entered into the grid below. Consider the four numbers that will appear in the shaded squares, on the same diagonal as the number How many of these four numbers are prime?
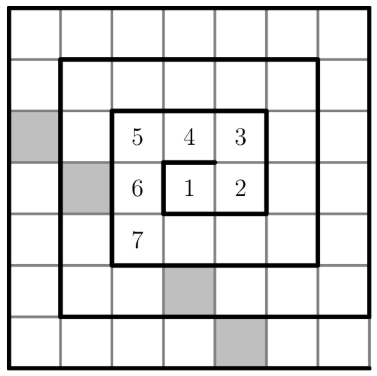
- A.
- B.
- C.
- D.
- E.
Solution 1
We fill out the grid, as shown below:
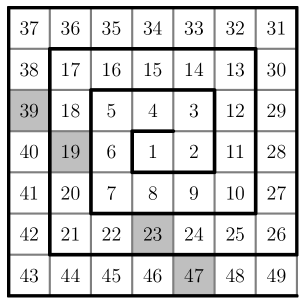
From the four numbers that appear in the shaded squares, of them are prime: and
Solution 2
Note that given time constraint, it's better to only count from perfect squares (in pink), as shown below:
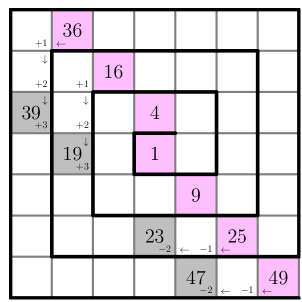
From the four numbers that appear in the shaded squares, of them are prime: and
A lake contains trout, along with a variety of other fish. When a marine biologist catches and releases a sample of fish from the lake, are identified as trout. Assume that the ratio of trout to the total number of fish is the same in both the sample and the lake. How many fish are there in the lake?
- A.
- B.
- C.
- D.
- E.
Note that
So, the total number of fish is times the number of trout. Since the lake contains trout, there are fish in the lake.
The digits and are placed in the expression below, one digit per box. What is the maximum possible value of the expression?
- A.
- B.
- C.
- D.
- E.
Solution 1
First, let us consider the case where is a base: This would result in the entire expression being Contrastingly, if is an exponent, we will get a value greater than is greater than and Therefore, the answer is
Solution 2
The maximum possible value of using the digits and : We can maximize our value by keeping the and together in one power (the biggest with the biggest and the smallest with the smallest). This shows (We don't want because that is .) It is going to be
A rectangle, with sides parallel to the -axis and -axis, has opposite vertices located at and . A line is drawn through points and . Another line is drawn through points and . How many points on the rectangle lie on at least one of the two lines?
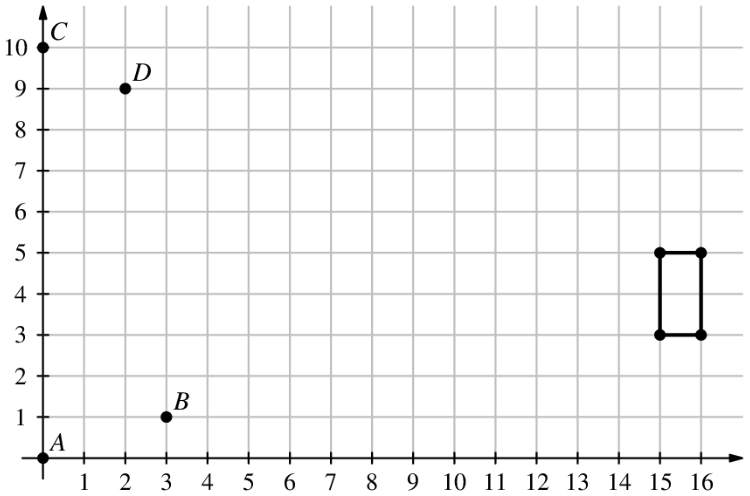
- A.
- B.
- C.
- D.
- E.
Solution 1
If we extend the lines, we have the following diagram:
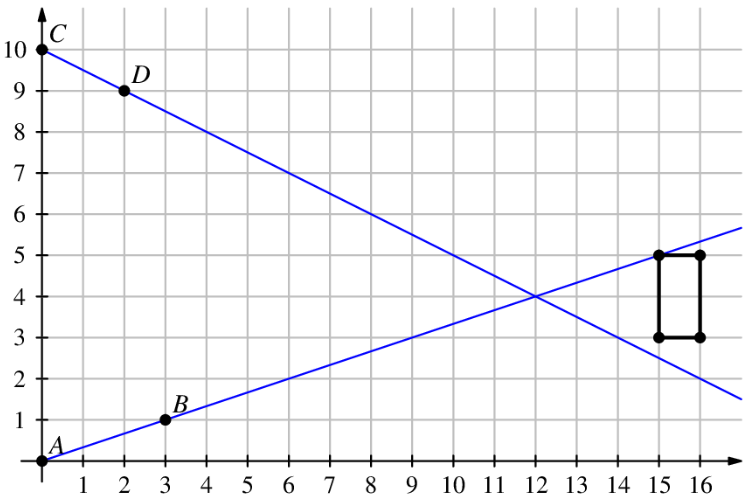
Therefore, we see that the answer is
Solution 2
Note that the -intercepts of line and line are and . If the analytic expression for line is , and the analytic expression for line is , we have equations: and . Solving these equations, we can find out that and . Therefore, we can determine that the expression for line is and the expression for line is . When , the coordinates that line and line pass through are and , and lies perfectly on one vertex of the rectangle while the coordinate of is out of the range (lower than the bottom left corner of the rectangle ). Considering that the value of the line will only decrease, and the value of the line will only increase, there will not be another point on the rectangle that lies on either of the two lines. Thus, we can conclude that the answer is
Lola, Lolo, Tiya, and Tiyo participated in a ping pong tournament. Each player competed against each of the other three players exactly twice. Shown below are the win-loss records for the players. The numbers and represent a win or loss, respectively. For example, Lola won five matches and lost the fourth match. What was Tiyo's win-loss record?

- A.
- B.
- C.
- D.
- E.
Solution 1
We can calculate the total number of wins ('s) by seeing how many matches were players, which is matches played. Then, we can calculate the # of wins already on the table, which is , so there are wins left in the mystery player. Now, we will make the key observation that there is only wins ('s) per column as there are winners and losers in each round. Strategically looking through the columns counting the 's and putting our own 's when the column isn't already full yields .
Solution 2
We can look one by one. We see that Lola and Lolo won the first game and Tiya lost. This shows that Tiyo must have lost as well because the results must be wins and loses. We use the same logic for games and , giving us 's again. We look at the choices, and we see A is the only that starts with 's.
This shows our answer is
Malaika is skiing on a mountain. The graph below shows her elevation, in meters, above the base of the mountain as she skis along a trail. In total, how many seconds does she spend at an elevation between and meters?
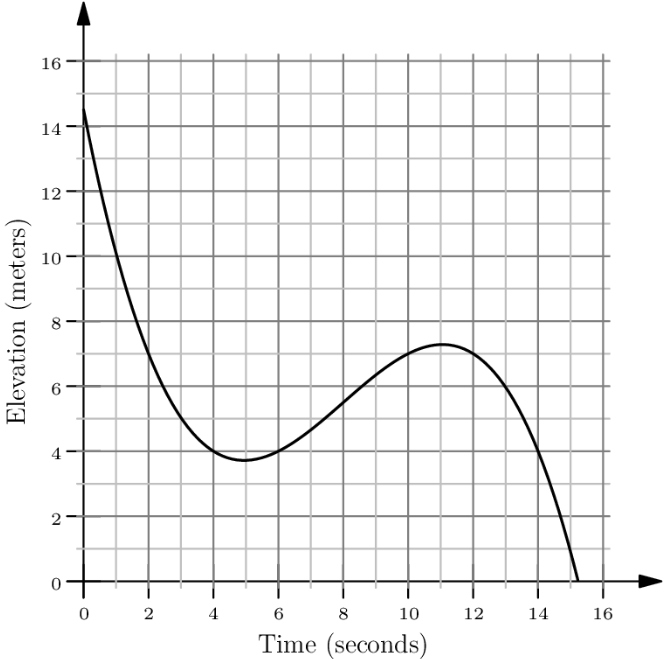
- A.
- B.
- C.
- D.
- E.
Solution 1
We mark the time intervals in which Malaika's elevation is between and meters in red, as shown below:

The requested time intervals are:
- from the nd to the th seconds - from the th to the th seconds - from the th to the th seconds In total, Malaika spends seconds at such elevation.
Solution 2
Notice that the entire section between the second mark and the second mark is between the and feet elevation level except the seconds where she skis just under the feet mark and when she skis just above the feet mark, making the answer
Harold made a plum pie to take on a picnic. He was able to eat only of the pie, and he left the rest for his friends. A moose came by and ate of what Harold left behind. After that, a porcupine ate of what the moose left behind. How much of the original pie still remained after the porcupine left?
- A.
- B.
- C.
- D.
- E.
Note that:
- Harold ate of the pie. After that, of the pie was left behind.
- The moose ate of the pie. After that, of the pie was left behind.
- The porcupine ate of the pie. After that, of the pie was left behind.
More simply, we can condense the solution above into the following equation:
NASA’s Perseverance Rover was launched on July After traveling miles, it landed on Mars in Jezero Crater about months later. Which of the following is closest to the Rover’s average interplanetary speed in miles per hour?
- A.
- B.
- C.
- D.
- E.
Solution 1
Note that months is approximately hours. Therefore, the speed (in miles per hour) is
As the answer choices are far apart from each other, we can ensure that the approximation is correct.
Solution 2
Note that miles. We also know that months is approximately hours. Now, we can calculate the speed in miles per hour, which we find is about
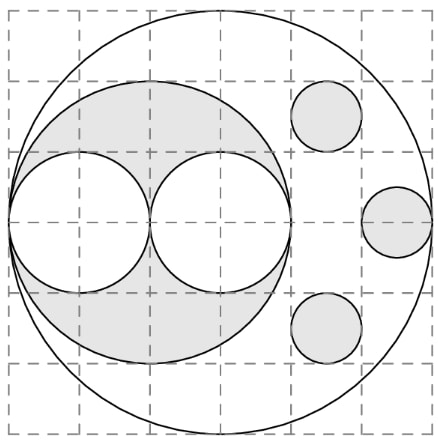
The figure below shows a large white circle with a number of smaller white and shaded circles in its interior. What fraction of the interior of the large white circle is shaded?
- A.
- B.
- C.
- D.
- E.
Solution 1
First, the total area of the radius circle is simply just when using our area of a circle formula.
Now from here, we have to find our shaded area. This can be done by adding the areas of the -radius circles and add; then, take the area of the radius circles and subtract that from the area of the radius circle to get our resulting complex shape area. Adding these up, we will get
.
So, our answer is .
Solution 2
Pretend each circle is a square. The large shaded circle is a square with area , and the two white circles inside it each have areas of , which adds up to . The three small shaded circles become three squares with area , and add up to . Adding the areas of the shaded circles (19) and subtracting the areas of the white circles (8), we get . Since the largest white circle in which all these other circles are becomes a square that has area , our answer is .
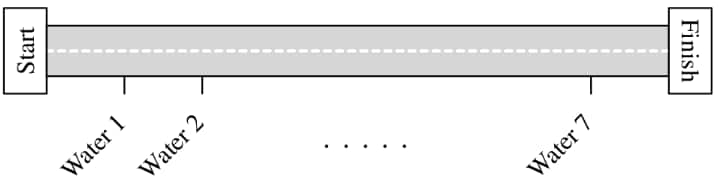
Along the route of a bicycle race, water stations are evenly spaced between the start and finish lines, as shown in the figure below. There are also repair stations evenly spaced between the start and finish lines. The rd water station is located miles after the st repair station. How long is the race in miles?
- A.
- B.
- C.
- D.
- E.
Suppose that the race is miles long. The water stations are located at
miles from the start, and the repair stations are located at
miles from the start.
We are given that from which
Nicolas is planning to send a package to his friend Anton, who is a stamp collector. To pay for the postage, Nicolas would like to cover the package with a large number of stamps. Suppose he has a collection of -cent, -cent, and -cent stamps, with exactly of each type. What is the greatest number of stamps Nicolas can use to make exactly in postage? (Note: The amount corresponds to dollars and cents. One dollar is worth cents.)
- A.
- B.
- C.
- D.
- E.
Solution 1
Let's use the most stamps to make We have of each stamp, -cent (nickels), -cent (dimes), and -cent (quarters).
If we want the highest number of stamps, we must have the highest number of the smaller value stamps (like the coins above). We can use nickels and dimes to bring our total cost to . However, when we try to use quarters, the cents don’t fit evenly, so we have to give back cents to make the quarter amount . The most efficient way to do this is to give back a -cent (dime) stamp and a -cent (nickel) stamp to have stamps used so far. Now, we just use quarters to get a grand total of .
Solution 2
The value of his entire stamp collection is dollars. To make with stamps, he should remove cents worth of stamps with as few stamps as possible. To do this, he should start by removing as many cent stamps as possible as they have the greatest denomination. He can remove at most of these stamps. He still has to remove cents worth of stamps. This can be done with one and cent stamp. In total, he has stamps in his entire collection. As a result, the maximum number of stamps he can use is .
Viswam walks half a mile to get to school each day. His route consists of city blocks of equal length and he takes minute to walk each block. Today, after walking blocks, Viswam discovers he has to make a detour, walking blocks of equal length instead of block to reach the next corner. From the time he starts his detour, at what speed, in mph, must he walk, in order to get to school at his usual time?

- A.
- B.
- C.
- D.
- E.
Solution 1
Note that Viswam walks at a constant speed of blocks per hour as he takes minute to walk each block. After walking blocks, he has taken minutes and has minutes remaining to walk blocks. Therefore, he must walk at a speed of blocks per hour to get to school on time, from the time he starts his detour. Since he normally walks mile, which is equal to blocks, mile is equal to blocks. Therefore, he must walk at mph from the time he starts his detour to get to school on time, so the answer is .
Solution 2
Viswam walks blocks, or half a mile, in minutes. Therefore, he walks at a rate of mph. When he takes his detour, he must travel blocks instead of . Our final equation is .
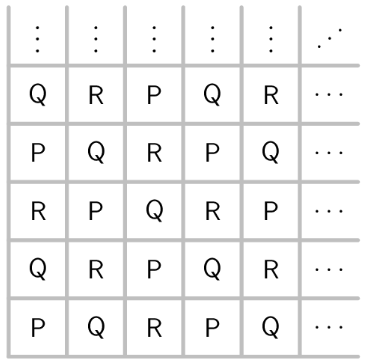
The letters and are entered into a table according to the pattern shown below. How many s, s, and s will appear in the completed table?
- A.
- B.
- C.
- D.
- E.
Solution 1
In our grid, there are and of the letters and , respectively, and in a grid, there are and of the letters and , respectively. We see that in both grids, there are and of the and , respectively. This is because in any grid with , there are and of the and , respectively. We can see that the only answer choice which satisfies this condition is
Solution 2
Since and is in the 2nd diagonal, it is also in the 20th diagonal, and so we find that there are . Since all the 's and 's are symmetric, the answer is
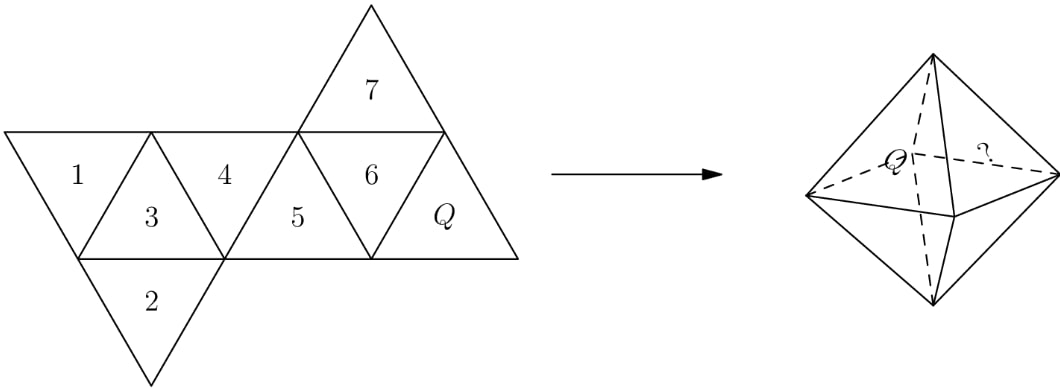
A regular octahedron has eight equilateral triangle faces with four faces meeting at each vertex. Jun will make the regular octahedron shown on the right by folding the piece of paper shown on the left. Which numbered face will end up to the right of ?
- A.
- B.
- C.
- D.
- E.
Solution 1
We color face red and face yellow. Note that from the octahedron, face and face do not share anything in common. From the net, face shares at least one vertex with all other faces except face which is shown in green:

Therefore, the answer is
Solution 2
We label the octohedron going triangle by triangle until we reach the triangle. The triangle to the left of the should be labeled with a . Underneath triangle is triangle . The triangle to the right of triangle is triangle and further to the right is triangle . Finally, the side of triangle under triangle is , so the triangle to the right of is .
Greta Grasshopper sits on a long line of lily pads in a pond. From any lily pad, Greta can jump pads to the right or pads to the left. What is the fewest number of jumps Greta must make to reach the lily pad located pads to the right of her starting position?
- A.
- B.
- C.
- D.
- E.
Solution 1
We have directions going right or left. We can assign a variable to each of these directions. We can call going right direction and we can call going left . We can build an equation of , where we have to limit the number of moves we do. We can do this by making more of our moves the move turn than the move turn. The first obvious step is to go some amount of moves in the right direction then subtract off in the left direction to land on . The least amount of ’s added to to make a multiple of is as . So now, we have solved the problem as we just go hops right, and just do 4 more hops left. Yielding as our answer.
Solution 2
Notice that , and jumping to the left increases the value of Greta's position by . Therefore, the number of jumps to the left must be . As the number of jumps to the left increases, so does the number of jumps to the right, we must minimize both, which occurs when we jump to the left and to the right. The answer is .
An equilateral triangle is placed inside a larger equilateral triangle so that the region between them can be divided into three congruent trapezoids, as shown below. The side length of the inner triangle is the side length of the larger triangle. What is the ratio of the area of one trapezoid to the area of the inner triangle?
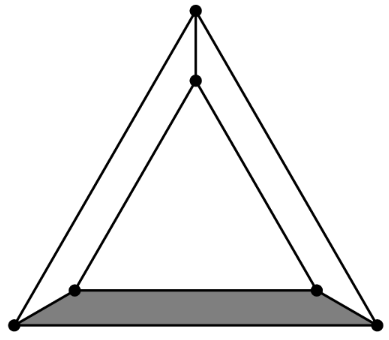
- A.
- B.
- C.
- D.
- E.
Solution 1
All equilateral triangles are similar. For the outer equilateral triangle to the inner equilateral triangle, since their side-length ratio is their area ratio is It follows that the area ratio of three trapezoids to the inner equilateral triangle is so the area ratio of one trapezoid to the inner equilateral triangle is
Solution 2
Subtracting the larger equilateral triangle from the smaller one yields the sum of the three trapezoids. Since the ratio of the side lengths of the larger to the smaller one is , we can set the side lengths as and , respectively. So, the sum of the trapezoids is . We are also told that the three trapezoids are congruent, thus the area of each of them is . Hence, the ratio is .
Two integers are inserted into the list to double its range. The mode and median remain unchanged. What is the maximum possible sum of the two additional numbers?
- A.
- B.
- C.
- D.
- E.
To double the range, we must find the current range, which is , to then double to: . Since we do not want to change the median, we need to get a value less than (as would change the mode) for the smaller, making fixed for the larger. Anything less than is not beneficial to the optimization because you want to get the largest range without changing the mode. So, taking our optimal values of and , we have an answer of .
Alina writes the numbers on separate cards, one number per card. She wishes to divide the cards into groups of cards so that the sum of the numbers in each group will be the same. In how many ways can this be done?
- A.
- B.
- C.
- D.
- E.
Solution 1
First, we need to find the sum of each group when split. This is the total sum of all the elements divided by the # of groups. . Then, dividing by , we have , so each group of must have a sum of 15. To make the counting easier, we will just see the possible groups 9 can be with. The possible groups 9 can be with 2 distinct numbers are and . Going down both of these avenues, we will repeat the same process for using the remaining elements in the list. Where there is only 1 set of elements getting the sum of , needs in both cases. After is decided, the remaining 3 elements are forced in a group, yielding us an answer of as our sets are and .
Solution 2
The group with must have the two other numbers adding up to , since the sum of all the numbers is . The sum of the numbers in each group must therefore be . We can have , , , or . With the first group, we have left over. The only way to form a group of numbers that add up to is with or . One of the possible arrangements is therefore . Then, with the second group, we have left over. With these numbers, there is no way to form a group of numbers adding to . Similarly, with the third group there is left over and we can make a group of numbers adding to with or . Another arrangement is . Finally, the last group has left over. There is no way to make a group of numbers adding to with this, so the arrangements are and . So, there are sets that can be formed.
In a sequence of positive integers, each term after the second is the product of the previous two terms. The sixth term is . What is the first term?
- A.
- B.
- C.
- D.
- E.
Solution 1
In this solution, we will use trial and error to solve. can be expressed as . We divide by and get , divide by and get , and divide by to get . No one said that they have to be in ascending order!
Solution 2
Consider the first term is and the second term is . Then, the following term will be , , and . Notice that , then we obtain and .
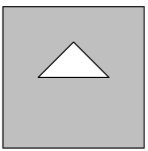
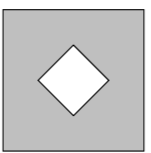
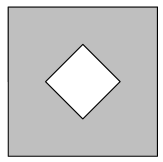
Each square in a grid is randomly filled with one of the gray and white tiles shown below on the right.
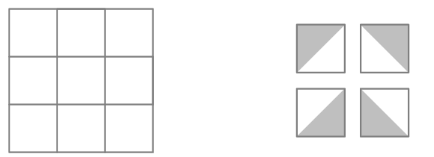
What is the probability that the tiling will contain a large gray diamond in one of the smaller grids? Below is an example of such tiling.

- A.
- B.
- C.
- D.
- E.
Solution 1
There are cases that the tiling will contain a large gray diamond in one of the smaller grids, as shown below:

There are ways to decide the white squares for each case, and the cases do not have any overlap.
So, the requested probability is
Solution 2
Note that the middle tile can be any of the four tiles. The gray part of the middle tile points towards one of the corners, and for the gray diamond to appear the three adjacent tiles must all be perfect. Thus, the solution is .
Isosceles has equal side lengths and . In the figure below, segments are drawn parallel to so that the shaded portions of have the same area. The heights of the two unshaded portions are 11 and 5 units, respectively. What is the height of of ? (Diagram not drawn to scale.)
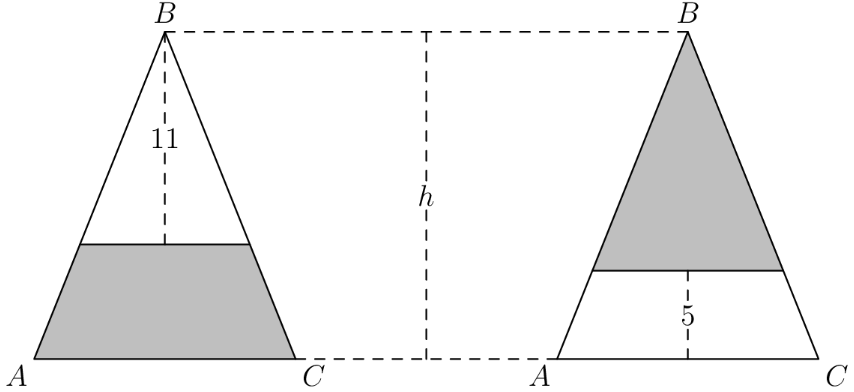
- A.
- B.
- C.
- D.
- E.
Solution 1
First, we notice that the smaller isosceles triangles are similar to the larger isosceles triangles. We can find that the area of the gray area in the first triangle is . Similarly, we can find that the area of the gray part in the second triangle is . These areas are equal, so . Simplifying yields so .
Solution 2
We can call the length of AC as . Therefore, the length of the base of the triangle with height is . Therefore, the base of the smaller triangle is . We find that the area of the trapezoid is .
Using similar triangles once again, we find that the base of the shaded triangle is . Therefore, the area is .
Since the areas are the same, we find that . Multiplying each side by , we get . Therefore, we can subtract from both sides, and get . Finally, we divide both sides by and get . is .
Fifteen integers are arranged in order on a number line. The integers are equally spaced and have the property that
What is the sum of digits of
- A.
- B.
- C.
- D.
- E.
Solution 1
We can find the possible values of the common difference by finding the numbers which satisfy the conditions. To do this, we find the minimum of the last two: , and the maximum–. There is a difference of between them, so only and work, as , so satisfies . The number is similarly found. , however, is too much.
Now, we check with the first and last equations using the same method. We know . Therefore, . We test both values we just got, and we can realize that is too large to satisfy this inequality. On the other hand, we can now find that the difference will be , which satisfies this inequality.
The last step is to find the first term. We know that the first term can only be from to since any larger value would render the second inequality invalid. Testing these three, we find that only will satisfy all the inequalities. Therefore, . The sum of the digits is therefore .
Solution 2
Let the common difference between consecutive be . Since , we find from the first and last inequalities that . As must be an integer, this means . Substituting this into all of the given inequalities so we may extract information about gives
The second inequality tells us that , while the last inequality tells us , so we must have . Finally, to solve for , we simply have , so our answer is .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
