2022 AMC 8
Complete problem set with solutions and individual problem pages
The Math Team designed a logo shaped like a multiplication symbol, shown below on a grid of -inch squares. What is the area of the logo in square inches?
- A.
- B.
- C.
- D.
- E.
Solution 1 (A quick solution)
We can see that there are 4 whole squares, since the area of each square will be , . Next, there are half squares, and half squares is whole square, so whole squares. The area of this will be . Finally, we can add the numbers: .
Solution 2
Draw the following four lines as shown:
We see these lines split the figure into five squares with side length . Thus, the area is
Consider these two operations:
What is the output of
- A.
- B.
- C.
- D.
- E.
We can find a general solution to any .
When three positive integers , , and are multiplied together, their product is . Suppose . In how many ways can the numbers be chosen?
- A.
- B.
- C.
- D.
- E.
Solution 1
The positive divisors of are
It is clear that so we apply casework to
- If then
- If then
- If then
- If then
Together, the numbers and can be chosen in ways.
Solution 2
The positive divisors of are
We apply casework to :
If , then there are cases:
-
-
-
If , then there is only case:
-
In total, there are ways to choose distinct positive integer values of .
The letter M in the figure below is first reflected over the line and then reflected over the line . What is the resulting image?
- A.
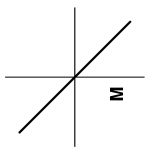
- B.
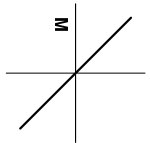
- C.
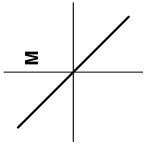
- D.
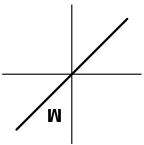
- E.
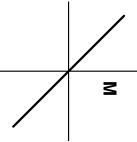
When M is first reflected over the line we obtain the following diagram:
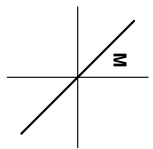
When M is then reflected over the line we obtain the following diagram:

Therefore, the answer is
Anna and Bella are celebrating their birthdays together. Five years ago, when Bella turned years old, she received a newborn kitten as a birthday present. Today the sum of the ages of the two children and the kitten is years. How many years older than Bella is Anna?
- A.
- B.
- C.
- D.
- E.
Five years ago, Bella was years old, and the kitten was years old.
Today, Bella is years old, and the kitten is years old. It follows that Anna is years old.
Therefore, Anna is years older than Bella.
Three positive integers are equally spaced on a number line. The middle number is and the largest number is times the smallest number. What is the smallest of these three numbers?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let the smallest number be It follows that the largest number is
Since and are equally spaced on a number line, we have
Solution 2
Let the common difference of the arithmetic sequence be . Consequently, the smallest number is and the largest number is . As the largest number is times the smallest number, . Finally, we find that the smallest number is .
When the World Wide Web first became popular in the s, download speeds reached a maximum of about kilobits per second. Approximately how many minutes would the download of a -megabyte song have taken at that speed? (Note that there are kilobits in a megabyte.)
- A.
- B.
- C.
- D.
- E.
Solution 1
Notice that the number of kilobits in this song is
We must divide this by in order to find out how many seconds this song would take to download:
Finally, we divide this number by because this is the number of seconds to get the answer
Solution 2
We seek a value of that makes the following equation true, since every other quantity equals .
Solving yields .
What is the value of
- A.
- B.
- C.
- D.
- E.
Solution 1
Note that common factors (from to inclusive) of the numerator and the denominator cancel. Therefore, the original expression becomes
Solution 2
The original expression becomes
A cup of boiling water () is placed to cool in a room whose temperature remains constant at . Suppose the difference between the water temperature and the room temperature is halved every minutes. What is the water temperature, in degrees Fahrenheit, after minutes?
- A.
- B.
- C.
- D.
- E.
Initially, the difference between the water temperature and the room temperature is degrees Fahrenheit.
After minutes, the difference between the temperatures is degrees Fahrenheit.
After minutes, the difference between the temperatures is degrees Fahrenheit.
After minutes, the difference between the temperatures is degrees Fahrenheit. At this point, the water temperature is degrees Fahrenheit.
Remark:
Alternatively, we can condense the solution above into the following equation:
One sunny day, Ling decided to take a hike in the mountains. She left her house at , drove at a constant speed of miles per hour, and arrived at the hiking trail at . After hiking for hours, Ling drove home at a constant speed of miles per hour. Which of the following graphs best illustrates the distance between Ling’s car and her house over the course of her trip?
- A.
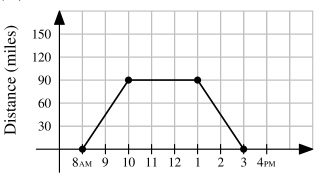
- B.
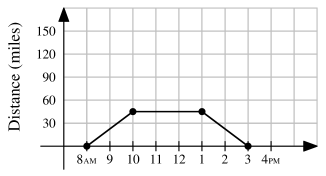
- C.
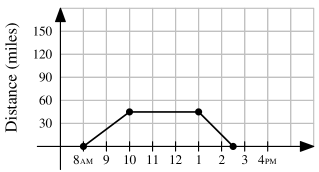
- D.
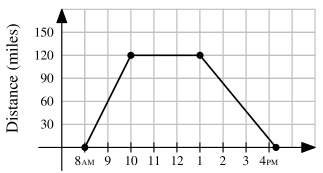
- E.
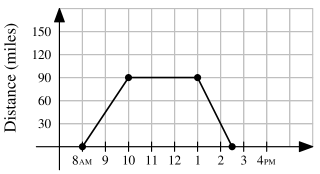
Solution 1 (Analysis) Note that:
- At Ling's car was miles from her house.
- From to Ling drove to the hiking trail at a constant speed of miles per hour.
It follows that at Ling's car was miles from her house.
- From to Ling did not move her car.
It follows that at Ling's car was still miles from her house.
- From Ling drove home at a constant speed of miles per hour. So, she arrived home hour later.
It follows that at Ling's car was miles from her house.
Therefore, the answer is
Solution 2 (Elimination)
Ling's trip took hours, thus she traveled for miles. Choices , , and are eliminated. Ling drove miles per hour (mph) to the mountains, and mph back to her house, so the rightmost slope must be steeper than the leftmost one. Choice is eliminated. This leaves us with .
Henry the donkey has a very long piece of pasta. He takes a number of bites of pasta, each time eating inches of pasta from the middle of one piece. In the end, he has pieces of pasta whose total length is inches. How long, in inches, was the piece of pasta he started with?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let's say that the first strand of pasta he had is . The first time he takes a bite of this strand will make it pieces. This is . The second time he takes the bites of EACH strand will become . The is for the two bites he took, for each strand. This equation is showing that for every bite that he is taking, he is taking off inches. This is being showed in the . He took bites, each taking off inches. Now, the problem is stating that their are pieces of pasta and the TOTAL length is inches. We have to plug in the total number of bites to the equation . To find this out, we can see that for the number of strands there are, he took less bite than that number. For example, if there are pieces, he took bite to get those. Since there are pieces, he took bites. The equation then becomes, . To solve this, . Therefore, the answer is .
Solution 2
If there are pieces of pasta, Henry took bites. Each of these bites took inches of pasta out, so all his bites in total took away inches of pasta. Thus, the original piece of pasta was inches long.
The arrows on the two spinners shown below are spun. Let the number equal times the number on Spinner , added to the number on Spinner . What is the probability that is a perfect square number?
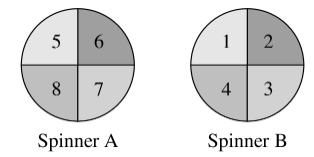
- A.
- B.
- C.
- D.
- E.
Solution 1
First, we calculate that there are a total of possibilities. Now, we list all of two-digit perfect squares. and are the only ones that can be made using the spinner. Consequently, there is a probability that the number formed by the two spinners is a perfect square.
Solution 2
There are total possibilities of . We know , which is a number from spinner , and is a number from spinner . Also, notice that there are no perfect squares in the s or s, so only values of N work, namely and . Hence, .
How many positive integers can fill the blank in the sentence below?
"One positive integer is more than twice another, and the sum of the two numbers is ."
- A.
- B.
- C.
- D.
- E.
Let and be positive integers such that and It follows that for some positive integer We wish to find the number of possible values for
By substitution, we have from which Note that each generate a positive integer for so there are possible values for
In how many ways can the letters in be rearranged so that two or more s do not appear together?
- A.
- B.
- C.
- D.
- E.
All valid arrangements of the letters must be of the form
The problem is equivalent to counting the arrangements of and into the four blanks, in which there are ways.
Laszlo went online to shop for black pepper and found thirty different black pepper options varying in weight and price, shown in the scatter plot below. In ounces, what is the weight of the pepper that offers the lowest price per ounce?
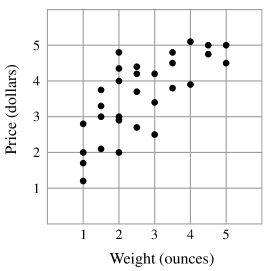
- A.
- B.
- C.
- D.
- E.
Solution 1
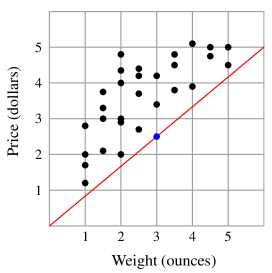
We are looking for a black point, that when connected to the origin, yields the lowest slope. The slope represents the price per ounce. We can visually find that the point with the lowest slope is the blue point. Furthermore, it is the only one with a price per ounce significantly less than . Finally, we see that the blue point is in the category with a weight of ounces.
Solution 2 (Elimination)
By the answer choices, we can disregard the points that do not have integer weights. As a result, we obtain the following diagram:
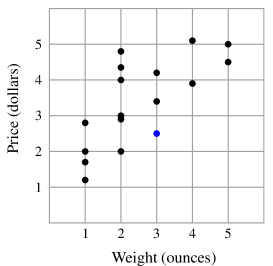
We then proceed in the same way that we had done in Solution . Following the steps, we figure out the blue dot that yields the lowest slope, along with passing the origin. We then can look at the x-axis(in this situation, the weight) and figure out it has ounces.
Four numbers are written in a row. The average of the first two is the average of the middle two is and the average of the last two is What is the average of the first and last of the numbers?
- A.
- B.
- C.
- D.
- E.
Solution 1 (Arithmetic)
Note that the sum of the first two numbers is the sum of the middle two numbers is and the sum of the last two numbers is
It follows that the sum of the four numbers is so the sum of the first and last numbers is Therefore, the average of the first and last numbers is
Solution 2 (Algebra)
Let and be the four numbers in that order. We are given that
and we wish to find
We add and then subtract from the result:
If is an even positive integer, the double factorial notation represents the product of all the even integers from to . For example, . What is the units digit of the following sum?
- A.
- B.
- C.
- D.
- E.
Solution 1
Notice that once the units digit of will be because there will be a factor of Thus, we only need to calculate the units digit of
We only care about units digits, so we have which has the same units digit as The answer is
Solution 2 (Solution 1 worded differently)
We can see that after in the sequence, the units digit is always (every value after is a multiple of ). Therefore, our answer is the sum of the units digits of and respectively. This sum is equal to , or
The midpoints of the four sides of a rectangle are and What is the area of the rectangle?
- A.
- B.
- C.
- D.
- E.
Solution 1
The midpoints of the four sides of every rectangle are the vertices of a rhombus whose area is half the area of the rectangle: Note that the diagonals of the rhombus have the same lengths as the sides of the rectangle.
Let and Note that and are the vertices of a rhombus whose diagonals have lengths and It follows that the dimensions of the rectangle are and so the area of the rectangle is
Solution 2
If a rectangle has area then the area of the quadrilateral formed by its midpoints is
Define points and as Solution 1 does. Since and are the midpoints of the rectangle, the rectangle's area is Now, note that is a parallelogram since and As the parallelogram's height from to is and its area is Therefore, the area of the rectangle is
Mr. Ramos gave a test to his class of students. The dot plot below shows the distribution of test scores.
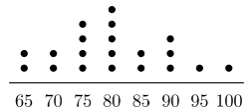
Later Mr. Ramos discovered that there was a scoring error on one of the questions. He regraded the tests, awarding some of the students extra points, which increased the median test score to . What is the minimum number of students who received extra points?
(Note that the median test score equals the average of the scores in the middle if the test scores are arranged in increasing order.)
- A.
- B.
- C.
- D.
- E.
We notice that students have scores under currently and only have scores over . We find the median of these two numbers, getting:
Thus, we realize that students must have their score increased by .
So, the correct answer is .
The grid below is to be filled with integers in such a way that the sum of the numbers in each row and the sum of the numbers in each column are the same. Four numbers are missing. The number in the lower left corner is larger than the other three missing numbers. What is the smallest possible value of ?
- A.
- B.
- C.
- D.
- E.
Solution 1
The sum of the numbers in each row is . Consider the second row. In order for the sum of the numbers in this row to equal , the two shaded numbers must add up to :
If two numbers add up to , one of them must be at least : If both shaded numbers are no more than , their sum can be at most . Therefore, for to be larger than the three missing numbers, must be at least . We can construct a working scenario where :
So, our answer is .
Solution 2
The sum of the numbers in each row is and the sum of the numbers in each column is
Let be the number in the lower middle. It follows that or
We express the other two missing numbers in terms of and as shown below:
We have and Note that the first inequality is true for all values of We only need to solve the second inequality so that the third inequality is true for all values of By substitution, we get from which
Therefore, the smallest possible value of is
Steph scored baskets out of attempts in the first half of a game, and baskets out of attempts in the second half. Candace took attempts in the first half and attempts in the second. In each half, Steph scored a higher percentage of baskets than Candace. Surprisingly they ended with the same overall percentage of baskets scored. How many more baskets did Candace score in the second half than in the first?
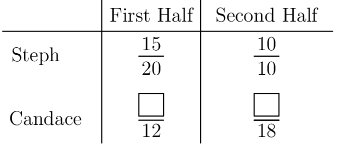
- A.
- B.
- C.
- D.
- E.
Solution 1 (Inequalities)
Let be the number of shots that Candace made in the first half, and let be the number of shots Candace made in the second half. Since Candace and Steph took the same number of attempts, with an equal percentage of baskets scored, we have In addition, we have the following inequalities:
and
Pairing this up with we see the only possible solution is for an answer of
Solution 2 (Answer Choices)
Clearly, Steph made shots in total. Also, due to parity reasons, the difference between the amount of shots Candace made in the first and second half must be odd. Thus, we can just test 7, 9, and 11, and after doing so we find that the answer is
A bus takes minutes to drive from one stop to the next, and waits minute at each stop to let passengers board. Zia takes minutes to walk from one bus stop to the next. As Zia reaches a bus stop, if the bus is at the previous stop or has already left the previous stop, then she will wait for the bus. Otherwise she will start walking toward the next stop. Suppose the bus and Zia start at the same time toward the library, with the bus stops behind. After how many minutes will Zia board the bus?

- A.
- B.
- C.
- D.
- E.
Solution 1
Initially, suppose that the bus is at Stop (starting point) and Zia is at Stop
We construct the following table of -minute intervals:
Note that Zia will wait for the bus after minutes, and the bus will arrive minutes later.
Therefore, the answer is
Solution 2
Since Zia will wait for the bus if the bus is at the previous stop, we can create an equation to solve for when the bus is at the previous stop. The bus travels of a stop per minute, and Zia travels of a stop per minute. Now we create the equation, (the accounts for us wanting to find when the bus reaches the stop before Zia's). Solving, we find that Now Zia has to wait minutes for the bus to reach her, so our answer is
A or is placed in each of the nine squares in a -by- grid. Shown below is a sample configuration with three s in a line.
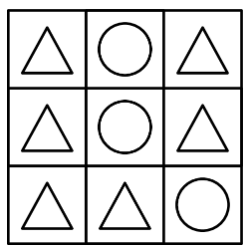
How many configurations will have three s in a line and three s in a line?
- A.
- B.
- C.
- D.
- E.
Solution 1 (Casework)
Notice that diagonals and a vertical-horizontal pair can never work, so the only possibilities are if all lines are vertical or if all lines are horizontal. These are essentially the same, so we'll count up how many work with all lines of shapes vertical, and then multiply by at the end.
We take casework:
Case : lines: In this case, the lines would need to be of one shape and of another, so there are ways to arrange the lines and ways to pick which shape has only one line. In total, this is
Case : lines: In this case, the lines would be one line of triangles, one line of circles, and the last one can be anything that includes both shapes. There are ways to arrange the lines and ways to choose the last line. (We subtract from the last line because one arrangement of the last line is all triangles and the other arrangement of the last line is all circles, which causes Case to overlap with Case and further complicating the solution.) In total, this is
Finally, we add and multiply: .
Solution 2 We will only consider cases where the three identical symbols are the same column, but at the end we shall double our answer as the same holds true for rows. There are ways to choose a column with all 's and ways to choose a column with all 's. The third column can be filled in ways. Therefore, we have a total of cases. However, we overcounted the cases with complete columns of with one symbol and complete column with another symbol. This happens in cases. . However, we have to remember to double our answer, giving us ways to complete the grid.
The figure below shows a polygon , consisting of rectangles and right triangles. When cut out and folded on the dotted lines, the polygon forms a triangular prism. Suppose that and . What is the volume of the prism?
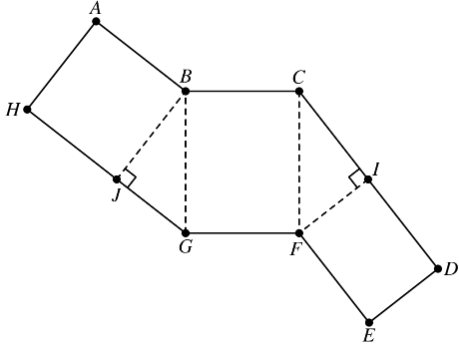
- A.
- B.
- C.
- D.
- E.
While imagining the folding, goes on goes on and goes on So, and Also, becomes an edge parallel to so that means
Since then So, the area of is If we let be the base, then the height is So, the volume is
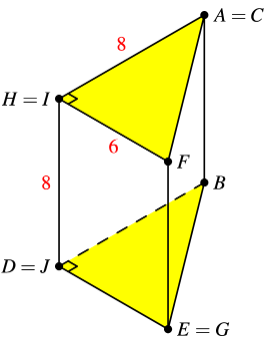
Remark
After folding polygon on the dotted lines, we obtain the following triangular prism:
A cricket randomly hops between leaves, on each turn hopping to one of the other leaves with equal probability. After hops what is the probability that the cricket has returned to the leaf where it started?
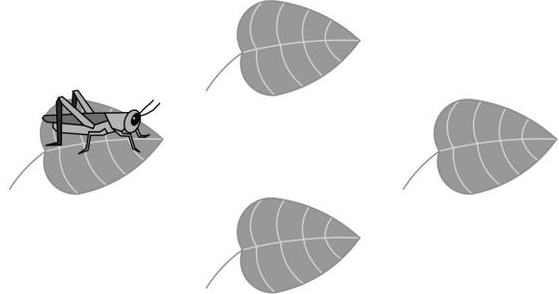
- A.
- B.
- C.
- D.
- E.
Solution 1 (Casework)
Let denote the leaf where the cricket starts and denote one of the other leaves. Note that:
- If the cricket is at then the probability that it hops to next is
- If the cricket is at then the probability that it hops to next is
- If the cricket is at then the probability that it hops to next is
We apply casework to the possible paths of the cricket:
.
The probability for this case is
.
The probability for this case is
Together, the probability that the cricket returns to after hops is
Solution 2 (Casework)
We can label the leaves as shown below:
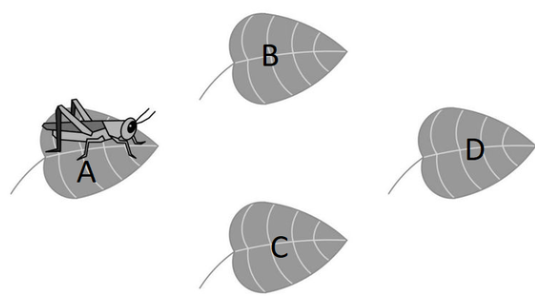
Carefully counting cases, we see that there are ways for the cricket to return to leaf after four hops if its first hop was to leaf :
.
.
.
.
.
.
.
By symmetry, we know that there are ways if the cricket's first hop was to leaf , and there are ways if the cricket's first hop was to leaf . So, there are ways in total for the cricket to return to leaf after four hops.
Since there are possible ways altogether for the cricket to hop to any other leaf four times, the answer is .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25







