2020 AMC 8
Complete problem set with solutions and individual problem pages
Luka is making lemonade to sell at a school fundraiser. His recipe requires times as much water as sugar and twice as much sugar as lemon juice. He uses cups of lemon juice. How many cups of water does he need?
- A.
- B.
- C.
- D.
- E.
Solution 1
We have so Luka needs cups.
Solution 2
Since the amount of sugar is twice the amount of lemon juice, Luka uses cups of sugar.
Since the amount of water is times the amount of sugar, he uses cups of water.
Four friends do yardwork for their neighbors over the weekend, earning and respectively. They decide to split their earnings equally among themselves. In total, how much will the friend who earned give to the others?
- A.
- B.
- C.
- D.
- E.
The friends earn in total. Since they decided to split their earnings equally, it follows that each person will get . Since the friend who earned will need to leave with , he will have to give to the others.
Carrie has a rectangular garden that measures feet by feet. She plants the entire garden with strawberry plants. Carrie is able to plant strawberry plants per square foot, and she harvests an average of strawberries per plant. How many strawberries can she expect to harvest?
- A.
- B.
- C.
- D.
- E.
Solution 1
Note that the unit of the answer is strawberries, which is the product of
- square feet
- plants per square foot
- strawberries per plant
By conversion factors, we have
Solution 2
The area of the garden is square feet. Since Carrie plants strawberry plants per square foot, there are a total of strawberry plants, each of which produces strawberries on average. Accordingly, she can expect to harvest strawberries.
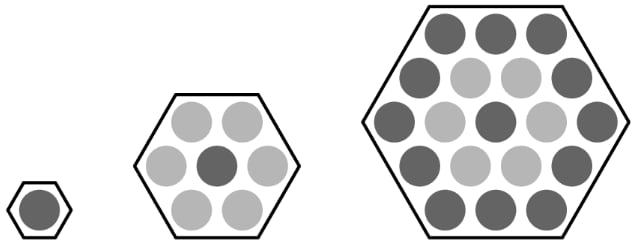
Three hexagons of increasing size are shown below. Suppose the dot pattern continues so that each successive hexagon contains one more band of dots. How many dots are in the next hexagon?
- A.
- B.
- C.
- D.
- E.
Solution 1
Looking at the rows of each hexagon, we see that the first hexagon has dot, the second has dots, and the third has dots. Given the way the hexagons are constructed, it is clear that this pattern continues. Hence, the fourth hexagon has dots.
Solution 2
The dots in the next hexagon have four bands. From innermost to outermost:
. The first band has dot.
. The second band has dots: dot at each vertex of the hexagon.
. The third band has dots: dot at each vertex of the hexagon and other dot on each edge of the hexagon.
. The fourth band has dots: dot at each vertex of the hexagon and other dots on each edge of the hexagon.
Together, the answer is
Three fourths of a pitcher is filled with pineapple juice. The pitcher is emptied by pouring an equal amount of juice into each of cups. What percent of the total capacity of the pitcher did each cup receive?
- A.
- B.
- C.
- D.
- E.
Solution 1
Each cup is filled with of the amount of juice in the pitcher, so the percentage is .
Solution 2
The pitcher is full, i.e. full. Therefore each cup receives percent of the total capacity.
Aaron, Darren, Karen, Maren, and Sharon rode on a small train that has five cars that seat one person each. Maren sat in the last car. Aaron sat directly behind Sharon. Darren sat in one of the cars in front of Aaron. At least one person sat between Karen and Darren. Who sat in the middle car?
- A.
- B.
- C.
- D.
- E.
Solution 1
Write the order of the cars as , where the left end of the row represents the back of the train and the right end represents the front. Call the people , , , , and respectively. The first condition gives , so we try , , and . In the first case, as sat in front of , we must have or , which do not comply with the last condition. In the second case, we obtain , which works, while the third case is obviously impossible since it results in there being no way for to sit in front of . It follows that, with the only possible arrangement being , the person sitting in the middle car is .
Solution 2
Follow the first few steps of Solution 1. We must have , and also have . There are only spaces available for , so the only possible arrangement of them is , so the arrangement is , so the person in the middle car is .
How many integers between and have four distinct digits arranged in increasing order? (For example, is one integer.).
- A.
- B.
- C.
- D.
- E.
Solution 1
Firstly, we can observe that the second digit of such a number cannot be or because the digits must be distinct and in increasing order. The second digit also cannot be as the number must be less than , so the second digit must be . It remains to choose the latter two digits, which must be distinct digits from . That can be done in ways; there is then only way to order the digits, namely in increasing order. This means the answer is .
Solution 2
As in Solution 1, we find that the first two digits must be , and the third digit must be at least because the digits can not repeat. If it is , then there are choices for the last digit, namely , , , , or . Similarly, if the third digit is , there are choices for the last digit, namely , , , and ; if , there are choices; if , there are choices; and if , there is choice. It follows that the total number of such integers is .
Ricardo has coins, some of which are pennies (-cent coins) and the rest of which are nickels (-cent coins). He has at least one penny and at least one nickel. What is the difference in cents between the greatest possible and least amounts of money that Ricardo can have?
- A.
- B.
- C.
- D.
- E.
Solution 1
Clearly, the amount of money Ricardo has will be maximized when he has the maximum number of nickels. Since he must have at least one penny, the greatest number of nickels he can have is , giving a total of cents. Analogously, the amount of money he has will be least when he has the greatest number of pennies; as he must have at least one nickel, the greatest number of pennies he can have is also , giving him a total of cents. Hence the required difference is
Solution 2
Suppose Ricardo has pennies, so then he has nickels. In order to have at least one penny and at least one nickel, we require and , i.e. . The number of cents he has is , so the maximum is and the minimum is , and the difference is therefore
Akash's birthday cake is in the form of a inch cube. The cake has icing on the top and the four side faces, and no icing on the bottom. Suppose the cake is cut into smaller cubes, each measuring inch, as shown below. How many of the small pieces will have icing on exactly two sides?

- A.
- B.
- C.
- D.
- E.
Solution 1
Notice that, for a small cube which does not form part of the bottom face, it will have exactly faces with icing on them only if it is one of the center cubes of an edge of the larger cube. There are such edges (as we exclude the edges of the bottom face), so this case yields small cubes. As for the bottom face, we can see that only the corner cubes have exactly faces with icing, so the total is .
Solution 2
The following diagram shows of the small cubes having exactly faces with icing on them; that is all of them except for those on the hidden face directly opposite the front face.
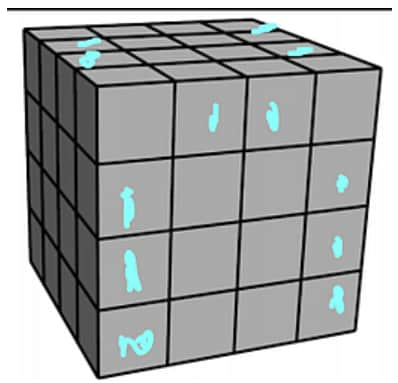
But the hidden face is an exact copy of the front face, so the answer is .
Zara has a collection of marbles: an Aggie, a Bumblebee, a Steelie, and a Tiger. She wants to display them in a row on a shelf, but does not want to put the Steelie and the Tiger next to one another. In how many ways can she do this?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let the Aggie, Bumblebee, Steelie, and Tiger, be referred to by and , respectively. If we ignore the constraint that and cannot be next to each other, we get a total of ways to arrange the 4 marbles. We now simply have to subtract out the number of ways that and can be next to each other. If we place and next to each other in that order, then there are three places that we can place them, namely in the first two slots, in the second two slots, or in the last two slots (i.e. ). However, we could also have placed and in the opposite order (i.e. ). Thus there are 6 ways of placing and directly next to each other. Next, notice that for each of these placements, we have two open slots for placing and . Specifically, we can place in the first open slot and in the second open slot or switch their order and place in the first open slot and in the second open slot. This gives us a total of ways to place and next to each other. Subtracting this from the total number of arrangements gives us total arrangements .
We can also solve this problem directly by looking at the number of ways that we can place and such that they are not directly next to each other. Observe that there are three ways to place and (in that order) into the four slots so they are not next to each other (i.e. ). However, we could also have placed and in the opposite order (i.e. ). Thus there are 6 ways of placing and so that they are not next to each other. Next, notice that for each of these placements, we have two open slots for placing and . Specifically, we can place in the first open slot and in the second open slot or switch their order and place in the first open slot and in the second open slot. This gives us a total of ways to place and such that they are not next to each other .
Solution 2
Let's try complementary counting. There ways to arrange the 4 marbles. However, there are arrangements where Steelie and Tiger are next to each other. (Think about permutations of the element ST, A, and B or TS, A, and B). Thus,
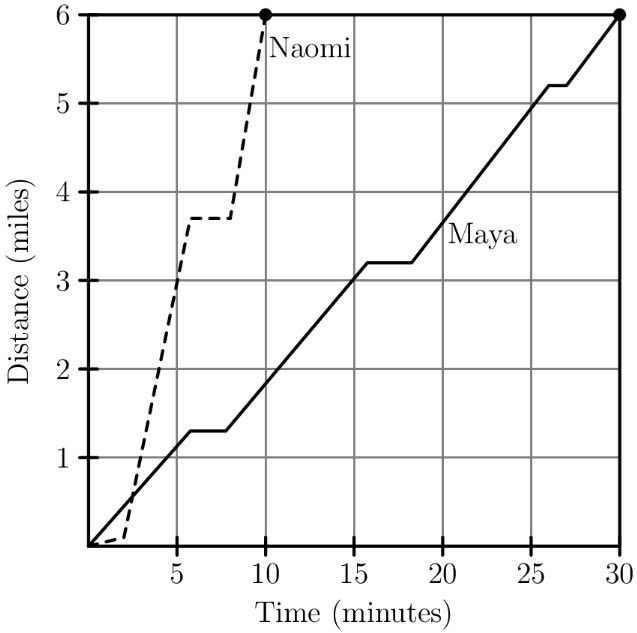
After school, Maya and Naomi headed to the beach, miles away. Maya decided to bike while Naomi took a bus. The graph below shows their journeys, indicating the time and distance traveled. What was the difference, in miles per hour, between Naomi's and Maya's average speeds?
- A.
- B.
- C.
- D.
- E.
Naomi travels miles in a time of minutes, which is equivalent to of an hour. Since , her speed is mph. By a similar calculation, Maya's speed is mph, so the answer is .
For a positive integer , the factorial notation represents the product of the integers from to . What value of satisfies the following equation?
- A.
- B.
- C.
- D.
- E.
We have , and . Therefore, the equation becomes , and so . Cancelling the s, it is clear that .
Jamal has a drawer containing green socks, purple socks, and orange socks. After adding more purple socks, Jamal noticed that there is now a chance that a sock randomly selected from the drawer is purple. How many purple socks did Jamal add?
- A.
- B.
- C.
- D.
- E.
Solution 1
After Jamal adds purple socks, he has purple socks and total socks. This means the probability of drawing a purple sock is , so we obtain
Since , the answer is .
Solution 2
green socks and orange socks together should be of the new total number of socks, so that new total must be . Therefore, purple socks were added.
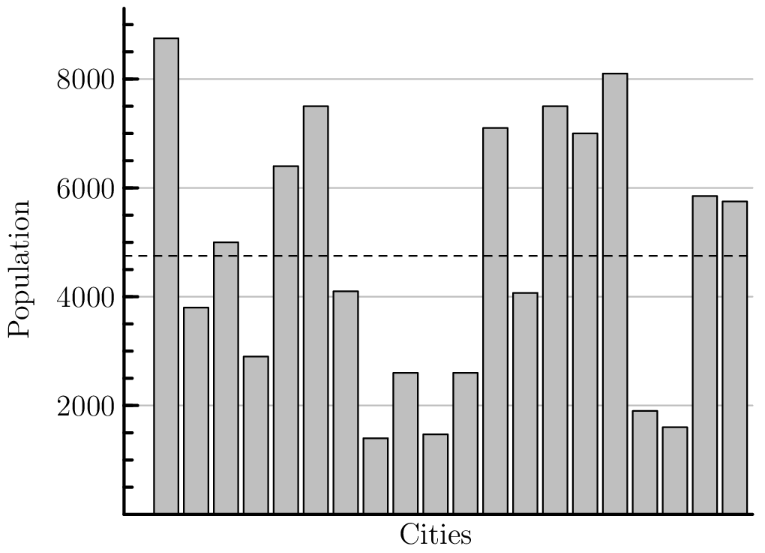
There are cities in the County of Newton. Their populations are shown in the bar chart below. The average population of all the cities is indicated by the horizontal dashed line. Which of the following is closest to the total population of all cities?
- A.
- B.
- C.
- D.
- E.
Solution 1
We can see that the dotted line is exactly halfway between and , so it is at . As this is the average population of all cities, the total population is simply .
Solution 2
The dotted line is slightly below . Since , the answer is slightly below this, so would be the best choice to guess.
Suppose of equals of What percentage of is
- A.
- B.
- C.
- D.
- E.
Solution 1
Since , multiplying the given condition by shows that is percent of .
Solution 2
Letting (without loss of generality), the condition becomes . Clearly, it follows that is of , so the answer is .
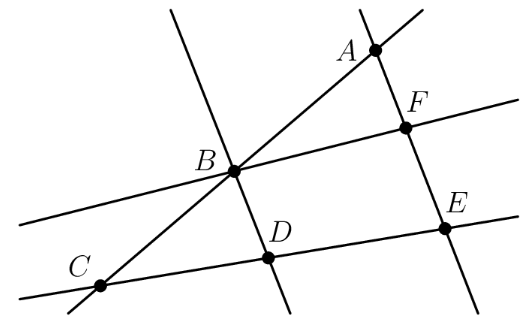
Each of the points and in the figure below represents a different digit from to Each of the five lines shown passes through some of these points. The digits along each line are added to produce five sums, one for each line. The total of the five sums is What is the digit represented by
- A.
- B.
- C.
- D.
- E.
Solution 1
We can form the following expressions for the sum along each line:
Adding these together, we must have , i.e. . Since are unique integers between and , we obtain (where the order doesn't matter as addition is commutative), so our equation simplifies to . This means .
Solution 2
Following the first few steps of Solution 1, we have . Because an even number subtracted from an odd number (47) is always odd, we know that is odd, showing that is odd. Now we know that is 1, 3, or 5. If we try , we get , which is false. Testing , we get , which is also false. Therefore, we have .
How many positive integer factors of have more than factors? (As an example, has factors, namely and )
- A.
- B.
- C.
- D.
- E.
Solution 1
Since , we can simply list its factors:
There are factors; only don't have over factors, so the remaining factors have more than factors.
Solution 2
As in Solution 1, we prime factorize as , and we recall the standard formula that the number of positive factors of an integer is found by adding to each exponent in its prime factorization, and then multiplying these. Thus has factors. The only number which has one factor is . For a number to have exactly two factors, it must be prime, and the only prime factors of are , , and . For a number to have three factors, it must be a square of a prime (this follows from the standard formula mentioned above), and from the prime factorization, the only square of a prime that is a factor of is . Thus, there are factors of which themselves have , , or factors (namely , , , , and ), so the number of factors of that have more than factors is .
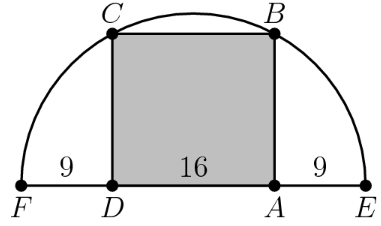
Rectangle is inscribed in a semicircle with diameter as shown in the figure. Let and let What is the area of .
- A.
- B.
- C.
- D.
- E.
Solution 1
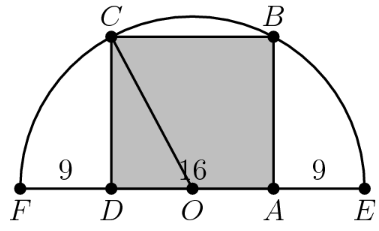
Let be the center of the semicircle. The diameter of the semicircle is , so . By symmetry, is the midpoint of , so . By the Pythagorean theorem in right-angled triangle (or ), we have that (or ) is . Accordingly, the area of is .
Solution 2
Let the midpoint of segment be the origin. Evidently, point and . Since points and share -coordinates with and respectively, it suffices to find the -coordinate of (which will be the height of the rectangle) and multiply this by (which we know is ). The radius of the semicircle is , so the whole circle has equation ; as already stated, has the same -coordinate as , i.e. , so substituting this into the equation shows that . Since at , the y-coordinate of is . Therefore, the answer is .
A number is called flippy if its digits alternate between two distinct digits. For example, and are flippy, but and are not. How many five-digit flippy numbers are divisible by
- A.
- B.
- C.
- D.
- E.
Solution 1
A number is divisible by precisely if it is divisible by and . The latter means the last digit must be either or , and the former means the sum of the digits must be divisible by . If the last digit is , the first digit would be (because the digits alternate), which is not possible. Hence the last digit must be , and the number is of the form . If the unknown digit is , we deduce . We know exists modulo because 2 is relatively prime to 3, so we conclude that (i.e. the second and fourth digit of the number) must be a multiple of . It can be , , , or , so there are options: , , , and .
Solution 2
After finding out that the last digit must be , the number is of the form . If the unknown digit is , we can find that one of the solutions to is , since is equal to , which is divisible by . After trying every one digit number, you'll notice that must be a multiple of , meaning that , , , or . , , , and are the solutions to this question.
A scientist walking through a forest recorded as integers the heights of trees standing in a row. She observed that each tree was either twice as tall or half as tall as the one to its right. Unfortunately some of her data was lost when rain fell on her notebook. Her notes are shown below, with blanks indicating the missing numbers. Based on her observations, the scientist was able to reconstruct the lost data. What was the average height of the trees, in meters?

- A.
- B.
- C.
- D.
- E.
Solution 1
We will show that , , , , and meters are the heights of the trees from left to right. We are given that all tree heights are integers, so since Tree 2 has height meters, we can deduce that Trees 1 and 3 both have a height of meters. There are now three possible cases for the heights of Trees 4 and 5 (in order for them to be integers), namely heights of and , and , or and . Checking each of these, in the first case, the average is meters, which doesn't end in as the problem requires. Therefore, we consider the other cases. With and , the average is meters, which again does not end in , but with and , the average is meters, which does. Consequently, the answer is .
Solution 2
Notice the average height of the trees ends with ; therefore, the sum of all five heights of the trees must end with or . ( = ) We already know Tree is meters tall. Both Tree and Tree must meters tall - since neither can be . Once again, apply our observation for solving for the Tree 's height. Tree can't be meters for the sum of the five tree heights to still end with . Therefore, the Tree is meters tall. Now, Tree can either be or . Find the average height for both cases of Tree . Doing this, we realize the Tree must be for the average height to end with and that the average height is .
A game board consists of squares that alternate in color between black and white. The figure below shows square in the bottom row and square in the top row. A marker is placed at A step consists of moving the marker onto one of the adjoining white squares in the row above. How many -step paths are there from to (The figure shows a sample path.)

- A.
- B.
- C.
- D.
- E.
Solution 1
Notice that, to step onto any particular white square, the marker must have come from one of the or white squares immediately beneath it (since the marker can only move on white squares). This means that the number of ways to move from to that square is the sum of the number of ways to move from to each of the white squares immediately beneath it (also called the Waterfall Method). To solve the problem, we can accordingly construct the following diagram, where each number in a square is calculated as the sum of the numbers on the white squares immediately beneath that square (and thus will represent the number of ways to remove from to that square, as already stated).

The answer is therefore .
Solution 2
Suppose we "extend" the chessboard infinitely with additional columns to the right, as shown below. The red line shows the right-hand edge of the original board.
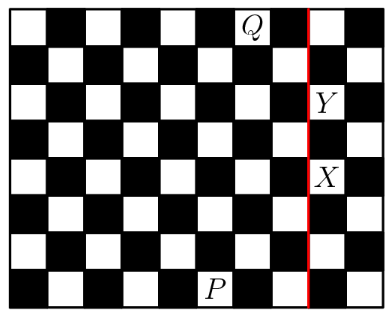
The total number of paths from to , including invalid paths which cross over the red line, is then the number of paths which make steps up-and-right and steps up-and-left, which is . We need to subtract the number of invalid paths, i.e. the number of paths that pass through or . To get to , the marker has to make up-and-right steps, after which it can proceed to with steps up-and-left and step up-and-right. Thus, the number of paths from to that pass through is . Similarly, the number of paths that pass through is . However, we have now double-counted the invalid paths which pass through both and ; from the diagram, it is clear that there are only of these (as the marker can get from to by a step up-and-left and a step-up-and-right in either order). Hence the number of invalid paths is , and the number of valid paths from to is .
When a positive integer is fed into a machine, the output is a number calculated according to the rule shown below.
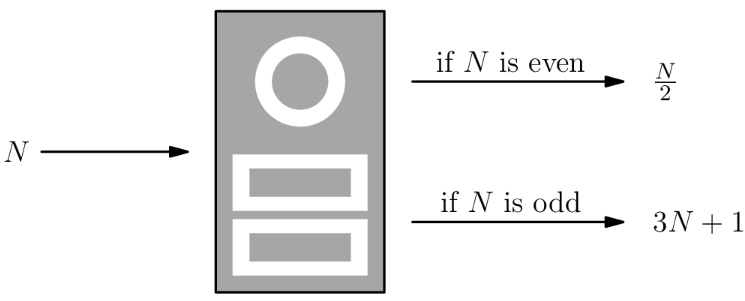
For example, starting with an input of the machine will output Then if the output is repeatedly inserted into the machine five more times, the final output is
When the same -step process is applied to a different starting value of the final output is What is the sum of all such integers
- A.
- B.
- C.
- D.
- E.
We start with final output of and work backward, taking cares to consider all possible inputs that could have resulted in any particular output. This produces following set of possibilities each stage:
where, for example, must come from (as there is no integer satisfying ), but could come from or (as , and is even while is odd). By construction, last set in this sequence contains all the numbers which will lead to number to end of the -step process, and sum is .
Five different awards are to be given to three students. Each student will receive at least one award. In how many different ways can the awards be distributed?
- A.
- B.
- C.
- D.
- E.
Firstly, observe that a single student can't receive or awards because this would mean that one of the other students receives no awards. Thus, each student must receive either , , or awards. If a student receives awards, then the other two students must each receive award; if a student receives awards, then another student must also receive awards and the remaining student must receive award. We consider each of these two cases in turn.
If a student receives three awards, there are ways to choose which student this is, and ways to give that student out of the awards. Next, there are students left and awards to give out, with each student getting one award. There are clearly just ways to distribute these two awards out, giving ways to distribute the awards in this case.
In the other case, two students receive awards and one student receives award. We know there are choices for which student gets award. There are ways to do this. Then, there are ways to give the first student his two awards, leaving awards yet to be distributed. There are then ways to give the second student his awards. Finally, there is only student and award left, so there is only way to distribute this award. This results in ways to distribute the awards in this case. Adding the results of these two cases, we get .
A large square region is paved with gray square tiles, each measuring inches on a side. A border inches wide surrounds each tile. The figure below shows the case for . When , the gray tiles cover of the area of the large square region. What is the ratio for this larger value of

- A.
- B.
- C.
- D.
- E.
Solution 1
The area of the shaded region is . To find the area of the large square, we note that there is a -inch border between each of the pairs of consecutive squares, as well as from between the first/last squares and the large square, for a total of times the length of the border, i.e. . Adding this to the total length of the consecutive squares, which is , the side length of the large square is , yielding the equation . Taking the square root of both sides (and using the fact that lengths are non-negative) gives , and cross-multiplying now gives .
Solution 2
WLOG (Without Loss of Generality), we may let (since will be determined by the scale of , and we are only interested in the ratio ). Then, as the total area of the gray tiles is simply , the large square has area , making the side of the large square . As in Solution 1, the side length of the large square consists of the total length of the gray tiles and lots of the border, so the length of the border is . Since if , the answer is .
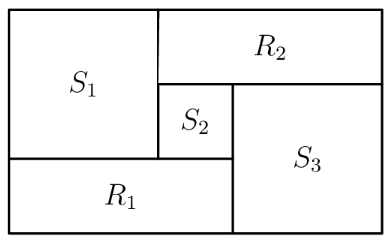
Rectangles and and squares and shown below, combine to form a rectangle that is 3322 units wide and 2020 units high. What is the side length of in units?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let the side length of each square be . Then, from the diagram, we can line up the top horizontal lengths of , , and to cover the top side of the large rectangle, so . Similarly, the short side of will be , and lining this up with the left side of to cover the vertical side of the large rectangle gives . We subtract the second equation from the first to obtain , and thus .
Solution 2
Assuming that the problem is well-posed, it should be true in the particular case where and . Let the sum of the side lengths of and be , and let the length of square be . We then have the system
which we solve to determine .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
