2019 AMC 8

Complete problem set with solutions and individual problem pages

Problem 1 Easy

Ike and Mike go into a sandwich shop with a total of $30.00 to spend. Sandwiches cost $4.50 each and soft drinks cost $1.00 each. Ike and Mike plan to buy as many sandwiches as they can, and use any remaining money to buy soft drinks. Counting both sandwiches and soft drinks, how many items will they buy?

  • A.

    6

  • B.

    7

  • C.

    8

  • D.

    9

  • E.

    10

Answer:D

Solution 1

We know that the sandwiches cost 4.50 dollars. Guessing will bring us to multiplying 4.50 by 6, which gives us 27.00. Since they can spend 30.00 they have 3 dollars left. Since soft drinks cost 1.00 dollar each, they can buy 3 soft drinks, which makes them spend 30.00 Since they bought 6 sandwiches and 3 soft drinks, they bought a total of 9 items. Therefore, the answer is \boxed{\textbf{(D) }9}.

 

Solution 2

Let s be the number of sandwiches and d be the number of sodas. We have to satisfy the equation of4.50s+d=30In the question, it states that Ike and Mike buys as many sandwiches as possible. So, we drop the number of sodas for a while. We have:

\begin{align*} 4.50s&=30 \\ s&=\frac{30}{4.5} \\ s&=6R3 \end{align*}

We don't want a remainder so the maximum number of sandwiches is 6. The total money spent is 6\cdot 4.50=27. The number of dollar left to spent on sodas is 30-27=3 dollars. 3 dollars can buy 3 sodas leading us to a total of 6+3=9 items. Hence, the answer is \boxed{\textbf{(D) }9}.

Link Problem
Problem 2 Easy

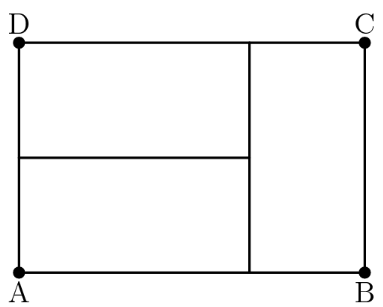
Three identical rectangles are put together to form rectangle ABCD, as shown in the figure below. Given that the length of the shorter side of each of the smaller rectangles is 5 feet, what is the area in square feet of rectangle ABCD?

  • A.

    45

  • B.

    75

  • C.

    100

  • D.

    125

  • E.

    150

Answer:E

Solution 1

We can see that there are 2 rectangles lying on top of the other and that is the same as the length of one rectangle. Now we know that the shorter side is 5, so the bigger side is 10, if we do 5 \cdot 2 = 10. Now we get the sides of the big rectangle being 15 and 10, so the area is \boxed{\textbf{(E)}\ 150}.

 

Solution 2

Using the diagram we find that the larger side of the small rectangle is 2 times the length of the smaller side. Therefore, the longer side is 5 \cdot 2 = 10. So the area of the identical rectangles is 5 \cdot 10 = 50. We have 3 identical rectangles that form the large rectangle. Therefore the area of the large rectangle is 50 \cdot 3 = \boxed{\textbf{(E)}\ 150}.

Link Problem
Problem 3 Easy

Which of the following is the correct order of the fractions \frac{15}{11},\frac{19}{15}, and \frac{17}{13}, from least to greatest?

  • A.

    \frac{15}{11}< \frac{17}{13}< \frac{19}{15}

  • B.

    \frac{15}{11}< \frac{19}{15}<\frac{17}{13}

  • C.

    \frac{17}{13}<\frac{19}{15}<\frac{15}{11}

  • D.

    \frac{19}{15}<\frac{15}{11}<\frac{17}{13}

  • E.

    \frac{19}{15}<\frac{17}{13}<\frac{15}{11}

Answer:E

Solution 1

We take a common denominator:

\frac{15}{11},\frac{19}{15}, \frac{17}{13} = \frac{15\cdot 15 \cdot 13}{11\cdot 15 \cdot 13},\frac{19 \cdot 11 \cdot 13}{15\cdot 11 \cdot 13}, \frac{17 \cdot 11 \cdot 15}{13\cdot 11 \cdot 15} = \frac{2925}{2145},\frac{2717}{2145},\frac{2805}{2145}.

Since 2717<2805<2925 it follows that the answer is \boxed{\textbf{(E)}\frac{19}{15}<\frac{17}{13}<\frac{15}{11}}.

 

Solution 2

When \frac{x}{y}>1 and z>0, \frac{x+z}{y+z}<\frac{x}{y}. Hence, the answer is \boxed{\textbf{(E)}\frac{19}{15}<\frac{17}{13}<\frac{15}{11}}.

Link Problem
Problem 4 Easy

Quadrilateral ABCD is a rhombus with perimeter 52 meters. The length of diagonal \overline{AC} is 24 meters. What is the area in square meters of rhombus ABCD?

  • A.

    60

  • B.

    90

  • C.

    105

  • D.

    120

  • E.

    144

Answer:D

Solution 1

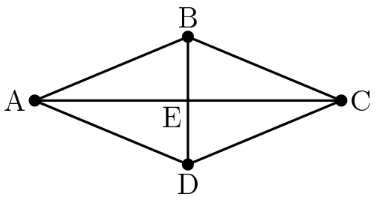
A rhombus has sides of equal length. Because the perimeter of the rhombus is 52, each side is \frac{52}{4}=13. In a rhombus, diagonals are perpendicular and bisect each other, which means \overline{AE} = 12 = \overline{EC}.

Consider one of the

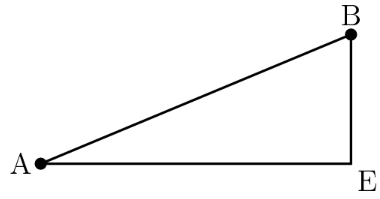
\overline{AB} = 13, and \overline{AE} = 12. Using the Pythagorean theorem, we find that \overline{BE} = 5. You know the Pythagorean triple (5, 12, 13).

Thus the values of the two diagonals are \overline{AC} = 24 and \overline{BD} = 10. The area of a rhombus is = \frac{d_1\cdot{d_2}}{2} = \frac{24\cdot{10}}{2} = 120

\boxed{\textbf{(D)}\ 120}

 

Solution 2

Right off the bat, we can see that the perimeter of the figure is 52. Dividing this by four, we can get that each side is equal to 13. By drawing a line perpendicular to the one given, we can split the figure into four right triangles. 12 (24/2) is equal to the height of one small right triangle, and 13 is the slanted side. Using the Pythagorean theorem we can find that 169 (13 squared) - 144 (12 squared) = 25 (five squared). With this, we can determine that each small right triangle equals 30. Multiplying that by four we can get \boxed{\textbf{(D)}\ 120}

Link Problem
Problem 5 Easy

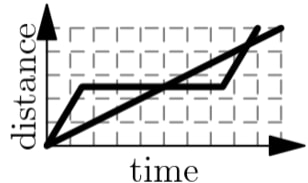
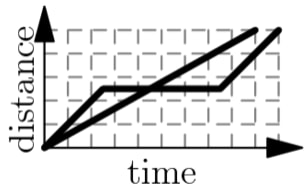
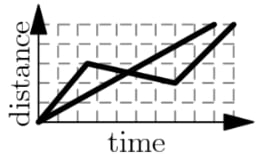
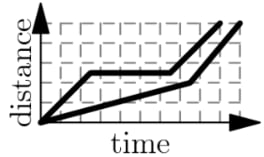
A tortoise challenges a hare to a race. The hare eagerly agrees and quickly runs ahead, leaving the slow-moving tortoise behind. Confident that he will win, the hare stops to take a nap. Meanwhile, the tortoise walks at a slow steady pace for the entire race. The hare awakes and runs to the finish line, only to find the tortoise already there. Which of the following graphs matches the description of the race, showing the distance d traveled by the two animals over time t from start to finish?

  • A.

  • B.

  • C.

  • D.

  • E.

Answer:B

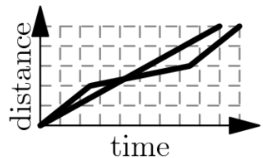
First, the tortoise walks at a constant rate, ruling out (D). Second, when the hare is resting, the distance will stay the same, ruling out (E) and (C). Third, the tortoise wins the race, meaning that the non-constant one should go off the graph last, ruling out (A). The answer \boxed{\textbf{(B)}} is the only one left.

Link Problem
Problem 6 Easy

There are 81 grid points (uniformly spaced) in the square shown in the diagram below, including the points on the edges. Point P is in the center of the square. Given that point Q is randomly chosen among the other 80 points, what is the probability that the line PQ is a line of symmetry for the square?

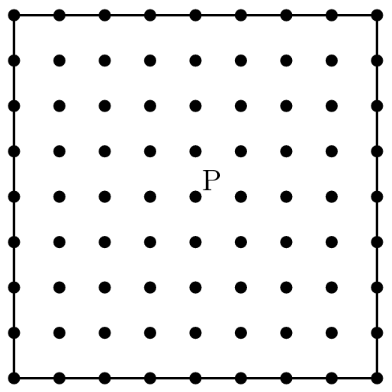
  • A.

    \frac15

  • B.

    \frac14

  • C.

    \frac25

  • D.

    \frac{9}{20}

  • E.

    \frac12

Answer:C

Solution 1

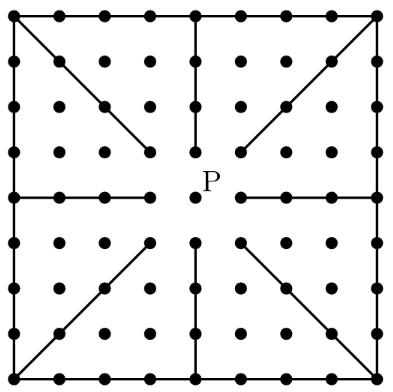
Lines of symmetry go through point P, and there are 8 directions the lines could go, and there are 4 dots at each direction.\frac{4\times8}{80}=\boxed{\textbf{(C)} \frac{2}{5}}.

 

Solution 2

Divide the grid into 4 4x5 quadrants. Each row of 5 points has 1 point on a horizontal/vertical line of symmetry + 1 point on a diagonal line of symmetry: \boxed{\textbf{(C)} \frac{2}{5}}.

Link Problem
Problem 7 Easy

Shauna takes five tests, each worth a maximum of 100 points. Her scores on the first three tests are 76 , 94 , and 87 . In order to average 81 for all five tests, what is the lowest score she could earn on one of the other two tests?

  • A.

    48

  • B.

    52

  • C.

    66

  • D.

    70

  • E.

    74

Answer:A

Solution 1

We should notice that we can turn the information we are given into a linear equation and just solve for our set variables. I'll use the variables x and y for the scores on the last two tests.

\frac{76+94+87+x+y}{5} = 81,

\frac{257+x+y}{5} = 81.

We can now cross multiply to get rid of the denominator.

257+x+y = 405,

x+y = 148.

Now that we have this equation, we will assign y as the lowest score of the two other tests, and so:

x = 100,

y=48.

Now we know that the lowest score on the two other tests is \boxed{48}.

 

Solution 2

Right now, she scored 76, 94, and 87 points, for a total of 257 points. She wants her average to be 81 for her 5 tests, so she needs to score 405 points in total. This means she needs to score a total of 405-257= 148 points in her next 2 tests. Since the maximum score she can get on one of her 2 tests is 100, the least possible score she can get is \boxed{\textbf{(A)}\ 48}.

Link Problem
Problem 8 Easy

Gilda has a bag of marbles. She gives 20\% of them to her friend Pedro. Then Gilda gives 10\% of what is left to another friend, Ebony. Finally, Gilda gives 25\% of what is now left in the bag to her brother Jimmy. What percentage of her original bag of marbles does Gilda have left for herself?

  • A.

    20

  • B.

    33 \frac13

  • C.

    38

  • D.

    45

  • E.

    54

Answer:E

Solution 1

After Gilda gives 20% of the marbles to Pedro, she has 80% of the marbles left. If she then gives 10% of what's left to Ebony, she has (0.8*0.9) = 72% of what she had at the beginning. Finally, she gives 25% of what's left to her brother, so she has (0.75*0.72) \boxed{\textbf{(E)}\ 54} of what she had in the beginning left.

 

Solution 2

WOLG, suppose that Gilda has 100 marbles.

Then, she gives Pedro 20% of 100, which equals 20, leaving her with 80 marbles.

Out of 80 marbles, she gives 10% of 80, which is 8 to Ebony.

Thus, she remains with 72 marbles.

Then, she gives 25% of 72, which equals 18 to Jimmy, finally leaving her with 54.

And, \frac{54}{100}=54%=\boxed{\textbf{(E)}\ 54}.

Link Problem
Problem 9 Easy

Alex and Felicia each have cats as pets. Alex buys cat food in cylindrical cans that are 6 cm in diameter and 12 cm high. Felicia buys cat food in cylindrical cans that are 12 cm in diameter and 6 cm high. What is the ratio of the volume of one of Alex's cans to the volume of one of Felicia's cans?

  • A.

    1:4

  • B.

    1:2

  • C.

    1:1

  • D.

    2:1

  • E.

    4:1

Answer:B

Solution 1

Using the formula for the volume of a cylinder, we get Alex, 108\pi, and Felicia, 216\pi. We can quickly notice that \pi cancels out on both sides and that Alex's volume is 1/2 of Felicia's leaving 1/2 = \boxed{\textbf{(B)}\ 1:2} as the answer.

 

Solution 2

Using the formula for the volume of a cylinder, we get that the volume of Alex's can is 3^2\cdot12\cdot\pi, and that the volume of Felicia's can is 6^2\cdot6\cdot\pi. Now, we divide the volume of Alex's can by the volume of Felicia's can, so we get \frac{1}{2}, which is \boxed{\textbf{(B)}\ 1:2}.

Link Problem
Problem 10 Easy

The diagram shows the number of students at soccer practice each weekday during last week. After computing the mean and median values, Coach discovers that there were actually 21 participants on Wednesday. Which of the following statements describes the change in the mean and median after the correction is made?

  • A.

    The mean increases by 1 and the median does not change.

  • B.

    The mean increases by 1 and the median increases by 1.

  • C.

    The mean increases by 1 and the median increases by 5.

  • D.

    The mean increases by 5 and the median increases by 1.

  • E.

    The mean increases by 5 and the median increases by 5.

Answer:B

On Monday, 20 people come. On Tuesday, 26 people come. On Wednesday, 16 people come. On Thursday, 22 people come. Finally, on Friday, 16 people come. 20+26+16+22+16=100, so the mean is 20. The median is (16, 16, 20, 22, 26) 20. The coach figures out that actually 21 people come on Wednesday. The new mean is 21, while the new median is (16, 20, 21, 22, 26) 21. Also, the median increases by 1 because now the median is 21 instead of 20. The median and mean both change, so the answer is \boxed{\textbf{(B)}}.

Link Problem
Problem 11 Medium

The eighth grade class at Lincoln Middle School has 93 students. Each student takes a math class or a foreign language class or both. There are 70 eighth graders taking a math class, and there are 54 eighth graders taking a foreign language class. How many eighth graders take only a math class and not a foreign language class?

  • A.

    16

  • B.

    53

  • C.

    31

  • D.

    39

  • E.

    70

Answer:D

Solution 1

Let x be the number of students taking both a math and a foreign language class.

By P-I-E, we get 70 + 54 - x = 93.

Solving gives us x = 31.

But we want the number of students taking only a math class,

which is 70 - 31 = 39.

\boxed{\textbf{(D)}\ 39}

 

Solution 2

We have 70 + 54 = 124 people taking classes. However, we over-counted the number of people who take both classes. If we subtract the original amount of people who take classes we get that 31 people took the two classes. To find the amount of people who took only math class, we subtract the people who didn't take only one math class, so we get 70 - 31 = \boxed{\textbf{(D)} \, 39}.

Link Problem
Problem 12 Medium

The faces of a cube are painted in six different colors: red (R), white (W), green (G), brown (B), aqua (A), and purple (P). Three views of the cube are shown below. What is the color of the face opposite the aqua face?

  • A.

    \text{ red}

  • B.

    \text{ white}

  • C.

    \text{ green}

  • D.

    \text{ brown}

  • E.

    \text{ purple}

Answer:A

B is on the top, and R is on the side, and G is on the right side. That means that (image 2) W is on the left side. From the third image, you know that P must be on the bottom since G is sideways. That leaves us with the back, so the back must be A. The front is opposite of the back, so the answer is \boxed{\textbf{(A)}\ R}.

Link Problem
Problem 13 Medium

A palindrome is a number that has the same value when read from left to right or from right to left. (For example, 12321 is a palindrome.) Let N be the least three-digit integer which is not a palindrome but which is the sum of three distinct two-digit palindromes. What is the sum of the digits of N?

  • A.

    2

  • B.

    3

  • C.

    4

  • D.

    5

  • E.

    6

Answer:A

Note that the only positive 2-digit palindromes are multiples of 11, namely 11, 22, \ldots, 99. Since N is the sum of 2-digit palindromes, N is necessarily a multiple of 11. The smallest 3-digit multiple of 11 which is not a palindrome is 110, so N=110 is a candidate solution. We must check that 110 can be written as the sum of three distinct 2-digit palindromes; this suffices as 110=77+22+11. Then, N = 110, and the sum of the digits of N is 1+1+0 = \boxed{\textbf{(A) }2}.

Link Problem
Problem 14 Medium

Isabella has 6 coupons that can be redeemed for free ice cream cones at Pete's Sweet Treats. In order to make the coupons last, she decides that she will redeem one every 10 days until she has used them all. She knows that Pete's is closed on Sundays, but as she circles the 6 dates on her calendar, she realizes that no circled date falls on a Sunday. On what day of the week does Isabella redeem her first coupon?

  • A.

    \text{Monday}

  • B.

    \text{Tuesday}

  • C.

    \text{Wednesday}

  • D.

    \text{Thursday}

  • E.

    \text{Friday}

Answer:C

Solution 1 

Let \text{Day }1 to \text{Day }2 denote a day where one coupon is redeemed and the day when the second coupon is redeemed.

If she starts on a \text{Monday}, she redeems her next coupon on \text{Thursday}.

\text{Thursday} to \text{Sunday}.

Thus, \textbf{(A)}\ \text{Monday} is incorrect.

If she starts on a \text{Tuesday}, she redeems her next coupon on \text{Friday}.

\text{Friday} to \text{Monday}.

\text{Monday} to \text{Thursday}.

\text{Thursday} to \text{Sunday}.

Thus \textbf{(B)}\ \text{Tuesday} is incorrect.

If she starts on a \text{Wednesday}, she redeems her next coupon on \text{Saturday}.

\text{Saturday} to \text{Tuesday}.

\text{Tuesday} to \text{Friday}.

\text{Friday} to \text{Monday}.

\text{Monday} to \text{Thursday}.

And on \text{Thursday}, she redeems her last coupon.

No Sunday occured; thus, \boxed{\textbf{(C)}\ \text{Wednesday}} is correct.

Checking for the other options,

If she starts on a \text{Thursday}, she redeems her next coupon on \text{Sunday}.

Thus, \textbf{(D)}\ \text{Thursday} is incorrect.

If she starts on a \text{Friday}, she redeems her next coupon on \text{Monday}.

\text{Monday} to \text{Thursday}.

\text{Thursday} to \text{Sunday}.

Checking for the other options gave us negative results; thus, the answer is \boxed{\textbf{(C)}\ \text{Wednesday}}.

 

Solution 2

Let

Sunday \equiv 0 \pmod{7}

Monday \equiv 1 \pmod{7}

Tuesday \equiv 2 \pmod{7}

Wednesday \equiv 3 \pmod{7}

Thursday \equiv 4 \pmod{7}

Friday \equiv 5 \pmod{7}

Saturday \equiv 6 \pmod{7}

10 \equiv 3 \pmod{7}

20 \equiv 6 \pmod{7}

30 \equiv 2 \pmod{7}

40 \equiv 5 \pmod{7}

50 \equiv 1 \pmod{7}

60 \equiv 4 \pmod{7}

Which indicates if you start from a x \equiv 3 \pmod{7} you will not get a y \equiv 0 \pmod{7}.

Any other starting value may lead to a y \equiv 0 \pmod{7}.

Which means our answer is \boxed{\textbf{(C) Wednesday}}.

Link Problem
Problem 15 Medium

On a beach 50 people are wearing sunglasses and 35 people are wearing caps. Some people are wearing both sunglasses and caps. If one of the people wearing a cap is selected at random, the probability that this person is also wearing sunglasses is \frac{2}{5}. If instead, someone wearing sunglasses is selected at random, what is the probability that this person is also wearing a cap?

  • A.

    \frac{14}{85}

  • B.

    \frac{7}{25}

  • C.

    \frac{2}{5}

  • D.

    \frac{4}{7}

  • E.

    \frac{7}{10}

Answer:B

Solution 1

The number of people wearing caps and sunglasses is \frac{2}{5}\cdot35=14. So then, 14 people out of the 50 people wearing sunglasses also have caps.

\frac{14}{50}=\boxed{\textbf{(B)}\frac{7}{25}}.

 

Solution 2

Let A be the event that a randomly selected person is wearing sunglasses, and let B be the event that a randomly selected person is wearing a cap. We can write P(A \cap B) in two ways: P(A)P(B|A) or P(B)P(A|B). Suppose there are t people in total. Then

P(A) = \frac{50}{t}

and

P(B) = \frac{35}{t}.

Additionally, we know that the probability that someone is wearing sunglasses given that they wear a cap is \frac{2}{5}, so P(A|B) = \frac{2}{5}. We let P(B|A), which is the quantity we want to find, be equal to x. Substituting in, we get

\frac{50}{t} \cdot x = \frac{35}{t} \cdot \frac{2}{5}\implies 50x = 35 \cdot \frac{2}{5}\implies 50x = 14\implies x = \frac{14}{50}= \boxed{\textbf{(B)}~\frac{7}{25}}

Link Problem
Problem 16 Hard

Qiang drives 15 miles at an average speed of 30 miles per hour. How many additional miles will he have to drive at 55 miles per hour to average 50 miles per hour for the entire trip?

  • A.

    45

  • B.

    62

  • C.

    90

  • D.

    110

  • E.

    135

Answer:D

Solution 1

The only option that is easily divisible by 55 is 110, which gives 2 hours of travel. And, the formula is \frac{15}{30} + \frac{110}{55} = \frac{5}{2}.

And, \text{Average Speed} = \frac{\text{Total Distance}}{\text{Total Time}}.

Thus, \frac{125}{50} = \frac{5}{2}.

Both are equal and thus our answer is \boxed{\textbf{(D)}\ 110}.

 

Solution 2

To calculate the average speed, simply evaluate the total distance over the total time. Let the number of additional miles he has to drive be x. Therefore, the total distance is 15+x and the total time (in hours) is

\frac{15}{30}+\frac{x}{55}=\frac{1}{2}+\frac{x}{55}.

We can set up the following equation:

\frac{15+x}{\frac{1}{2}+\frac{x}{55}}=50.

Simplifying the equation, we get

15+x=25+\frac{10x}{11}.

Solving the equation yields x=110, so our answer is \boxed{\textbf{(D)}\ 110}.

Link Problem
Problem 17 Hard

What is the value of the product

\left(\frac{1\cdot3}{2\cdot2}\right)\left(\frac{2\cdot4}{3\cdot3}\right)\left(\frac{3\cdot5}{4\cdot4}\right)\cdots\left(\frac{97\cdot99}{98\cdot98}\right)\left(\frac{98\cdot100}{99\cdot99}\right)?

  • A.

    \frac{1}{2}

  • B.

    \frac{50}{99}

  • C.

    \frac{9800}{9801}

  • D.

    \frac{100}{99}

  • E.

    50

Answer:B

Solution 1

We rewrite:

\frac{1}{2}\cdot\left(\frac{3\cdot2}{2\cdot3}\right)\left(\frac{4\cdot3}{3\cdot4}\right)\cdots\left(\frac{99\cdot98}{98\cdot99}\right)\cdot\frac{100}{99}

The middle terms cancel, leaving us with

\left(\frac{1\cdot100}{2\cdot99}\right)= \boxed{\textbf{(B)}\frac{50}{99}}

 

Solution 2

If you calculate the first few values of the equation, all of the values tend to close to \frac{1}{2}, but are not equal to it. The answer closest to \frac{1}{2} but not equal to it is \boxed{\textbf{(B)}\frac{50}{99}}.

Link Problem
Problem 18 Hard

The faces of each of two fair dice are numbered 1, 2, 3, 5, 7, and 8. When the two dice are tossed, what is the probability that their sum will be an even number?

  • A.

    \frac49

  • B.

    \frac12

  • C.

    \frac59

  • D.

    \frac35

  • E.

    \frac 23

Answer:C

Solution 1

We have 2 dice with 2 evens and 4 odds on each die. For the sum to be even, the 2 rolls must be 2 odds or 2 evens.

Ways to roll 2 odds (Case 1): The total number of ways to obtain 2 odds on 2 rolls is 4*4=16, as there are 4 possible odds on the first roll and 4 possible odds on the second roll.

Ways to roll 2 evens (Case 2): Similarly, we have 2*2=4 ways to obtain 2 evens. Probability is \frac{20}{36}=\frac{5}{9}, or \boxed{C}.

 

Solution 2

We count the ways to get an odd. If the sum is odd, then we must have an even and an odd. The probability of an even is \frac{1}{3} , and the probability of an odd is \frac{2}{3}. We have to multiply by 2 because the even and odd can be in any order. This gets us \frac{4}{9}, so the answer is 1 - \frac{4}{9} = \frac{5}{9} = \boxed{(\textbf{C})}.

Link Problem
Problem 19 Hard

In a tournament there are six teams that play each other twice. A team earns 3 points for a win, 1 point for a draw, and 0 points for a loss. After all the games have been played it turns out that the top three teams earned the same number of total points. What is the greatest possible number of total points for each of the top three teams?

  • A.

    22

  • B.

    23

  • C.

    24

  • D.

    26

  • E.

    30

Answer:C

Solution 1

We can name the top three teams as A, B, and C. We can see that (respective scores of) A=B=C because these teams have the same points. If we look at the matches that involve the top three teams, we see that there are some duplicates: AB, BC, and AC come twice. In order to even out the scores and get the maximum score, we can say that in match AB, A and B each win once out of the two games that they play. We can say the same thing for AC and BC. This tells us that each team A, B, and C win and lose twice. This gives each team a total of 3 + 3 + 0 + 0 = 6 points. Now, we need to include the other three teams. We can label these teams as D, E, and F. We can write down every match that A, B, or C plays in that we haven't counted yet: AD, AD, AE, AE, AF, AF, BD, BD, BE, BE, BF, BF, CD, CD, CE, CE, CF, and CF. We can say A, B, and C win each of these in order to obtain the maximum score that A, B, and C can have. If A, B, and C win all six of their matches, A, B, and C will have a score of 18. 18 + 6 results in a maximum score of \boxed{\textbf{(C) }24}

 

Solution 2

To start, we calculate how many games each team plays. Each team can play against 5 other teams twice, so there are 10 games that each team plays. So the answer is 10\cdot 3 which is 30 But wait \cdots if we want 3 teams to have the same amount of points, there can't possibly be a team who wins all their games. Let the top three teams be A,B, and C. A plays B and C twice, so in order to maximize the games being played, we can split it 50-50 between the 4 games A plays against B or C. We find that we just subtract 2 games or 6 points. Therefore the answer is 30-6, 24 or \boxed{\textbf{(C) }24}

Link Problem
Problem 20 Hard

How many different real numbers x satisfy the equation

(x^{2}-5)^{2}=16?

  • A.

    0

  • B.

    1

  • C.

    2

  • D.

    4

  • E.

    8

Answer:D

Solution 1

We have that (x^2-5)^2 = 16 if and only if x^2-5 = \pm 4. If x^2-5 = 4, then x^2 = 9 \implies x = \pm 3, giving 2 solutions. If x^2-5 = -4, then x^2 = 1 \implies x = \pm 1, giving 2 more solutions. All four of these solutions work, so the answer is \boxed{\textbf{(D) }4}. Further, the equation is a quartic in x, so by the Fundamental Theorem of Algebra, there can be at most four real solutions.

 

Solution 2

We can expand (x^2-5)^2 to get x^4-10x^2+25, so now our equation is x^4-10x^2+25=16. Subtracting 16 from both sides gives us x^4-10x^2+9=0. Now, we can factor the left-hand side to get (x^2-9)(x^2-1)=0. If x^2-9 and/or x^2-1 equals 0, then the entire left side will equal 0. Since the solutions can be both positive and negative, we have 4 solutions: -3,3,-1,1 (we can find these solutions by setting x^2-9 and x^2-1 equal to 0 and solving for x). So, the answer is \boxed{\textbf{(D) }4}.

Link Problem
Problem 21 Hard

What is the area of the triangle formed by the lines y=5, y=1+x, and y=1-x?

  • A.

    4

  • B.

    8

  • C.

    10

  • D.

    12

  • E.

    16

Answer:E

First, we need to find the coordinates where the graphs intersect.

We want the points x and y to be the same. Thus, we set 5=x+1, and get x=4. Plugging this into the equation, y=1-x, y=5, and y=1+x intersect at (4,5), we call this line x.

Doing the same thing, we get x=-4. Thus, y=5. Also, y=5 and y=1-x intersect at (-4,5), and we call this line y.

It's apparent the only solution to 1-x=1+x is 0. Thus, y=1. y=1-x and y=1+x intersect at (0,1), we call this line z.

Using the Shoelace Theorem we get:

\left(\frac{(20-4)-(-20+4)}{2}\right)=\frac{32}{2}= So, our answer is \boxed{\textbf{(E)}\ 16.}

We might also see that the lines y and x are mirror images of each other. This is because, when rewritten, their slopes can be multiplied by -1 to get the other. As the base is horizontal, this is an isosceles triangle with base 8, as the intersection points have a distance of 8. The height is 5-1=4, so \frac{4\cdot 8}{2} = \boxed{\textbf{(E)} 16.}

Link Problem
Problem 22 Hard

A store increased the original price of a shirt by a certain percent and then lowered the new price by the same amount. Given that the resulting price was 84\% of the original price, by what percent was the price increased and decreased?

  • A.

    16

  • B.

    20

  • C.

    28

  • D.

    36

  • E.

    40

Answer:E

Solution 1

Suppose the fraction of discount is x. That means (1-x)(1+x)=0.84; so, 1-x^{2}=0.84, and (x^{2})=0.16, procuring x=0.4. Therefore, the price was increased and decreased by 40%, or \boxed{\textbf{(E)}\ 40}.

 

Solution 2

Let x be the discount. We can also work in reverse such as (84)(\frac{100}{100-x})(\frac{100}{100+x}) = 100.

Thus, 8400 = (100+x)(100-x). Solving for x gives us x = 40, -40. But x has to be positive. Thus, x = 40.

Link Problem
Problem 23 Hard

After Euclid High School's last basketball game, it was determined that \frac{1}{4} of the team's points were scored by Alexa and \frac{2}{7} were scored by Brittany. Chelsea scored 15 points. None of the other 7 team members scored more than 2 points. What was the total number of points scored by the other 7 team members?

  • A.

    10

  • B.

    11

  • C.

    12

  • D.

    13

  • E.

    14

Answer:B

Solution 1

Given the information above, we start with the equation \frac{t}{4}+\frac{2t}{7} + 15 + x = t, where t is the total number of points scored and x\leqslant 14 is the number of points scored by the remaining 7 team members, we can simplify to obtain the Diophantine equation x+15 = \frac{13}{28}t, or 28x+28\cdot 15=13t. Since t is necessarily divisible by 28, let t=28u where u \geqslant 0 and divide by 28 to obtain x + 15 = 13u. Then, it is easy to see u=2 (t=56) is the only candidate remaining, giving x=\boxed{\textbf{(B)} 11}.

 

Solution 2

We first start by setting the total number of points as 28, since \text{LCM}(4,7) = 28. However, we see that this does not work since we surpass the number of points just with the information given (28\cdot\frac{1}{4}+28\cdot\frac{2}{7} + 15 = 30 (> 28) ). Next, we can see that the total number of points scored is 56 as, if it is more than or equal to 84, at least one of the others will score more than 2 points. With this, we have that Alexa, Brittany, and Chelsea score: 56\cdot\frac{1}{4}+56\cdot\frac{2}{7} + 15 = 45, and thus, the other seven players would have scored a total of 56-45 = \boxed{\textbf{(B)} 11}.

Link Problem
Problem 24 Hard

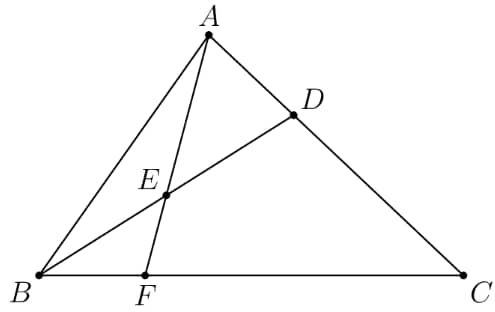
In triangle \triangle ABC, point D divides side \overline{AC} so that AD:DC=1:2. Let E be the midpoint of \overline{BD} and let F be the point of intersection of line \overline{BC} and line \overline{AE}. Given that the area of \triangle ABC is 360, what is the area of \triangle EBF?

  • A.

    24

  • B.

    30

  • C.

    32

  • D.

    36

  • E.

    40

Answer:B

Solution 1

We use the line-segment ratios to infer area ratios and height ratios.

Areas:

AD:DC = 1:2 \implies AD:AC = 1:3 \implies [ABD] =\frac{[ABC]}{3} = 120.

BE:BD = 1:2 \text{ (midpoint)} \implies [ABE] = \frac{[ABD]}{2} = \frac{120}{2} = 60.

Heights:

Let h_A = height (of altitude) from \overline{BC} to A.

AD:DC = 1:2 \implies CD:CA = 2:3 \implies \text{height } h_D from \overline{BC} to D is \frac{2}{3}h_A.

BE:BD = 1:2 \text{ (midpoint)} \implies \text{height } h_E from \overline{BC} to E is \frac{1}{2} h_D = \frac{1}{2}(\frac{2}{3} h_A) = \frac{1}{3} h_A.

Conclusion:

\frac{[EBF]} {[ABF]} = \frac{[EBF]} {[EBF] + [ABE]} = \frac{[EBF]} {[EBF]+60}, and also \frac{[EBF]} {[ABF]} = \frac{h_E}{h_A} = \frac{1}{3}.

So, \frac{[EBF]} {[EBF] + 60} = \frac{1}{3}, and thus, [EBF] = \boxed{\textbf{(B) }30}

 

Solution 2

Draw X on \overline{AF} such that \overline{XD} is parallel to \overline{BC}.

Triangles BEF and EXD are similar, and since BE = ED, they are also congruent, and so XE=EF and XD=BF.

AC:AD = 3 implies \frac{AF}{AX} = 3 = \frac{FC}{XD} = \frac{FC}{BF}, so BC=BF + 3BF = 4BF, BF=\frac{BC}{4}.

Since XE=EF, AX = XE = EF, and since AX + XE + EF = AF, all of these are equal to \frac{AF}{3}, and so the altitude of triangle BEF is equal to \frac{1}{3} of the altitude of ABC.

The area of ABC is 360, so the area of\triangle EBF=\frac{1}{3} \cdot \frac{1}{4} \cdot 360=\boxed{\textbf{(B) }30}.

Link Problem
Problem 25 Hard

Alice has 24 apples. In how many ways can she share them with Becky and Chris so that each of the three people has at least two apples?

  • A.

    105

  • B.

    114

  • C.

    190

  • D.

    210

  • E.

    380

Answer:C

Solution 1 

Note: This solution uses the non-negative version for stars and bars. A solution using the positive version of stars is similar (first removing an apple from each person instead of 2).

This method uses the counting method of stars and bars (non-negative version). Since each person must have at least 2 apples, we can remove 2*3 apples from the total that need to be sorted. With the remaining 18 apples, we can use stars and bars to determine the number of possibilities. Assume there are 18 stars in a row, and 2 bars, which will be placed to separate the stars into groups of 3. In total, there are 18 spaces for stars + 2 spaces for bars, for a total of 20 spaces. We can now do 20 \choose 2. This is because if we choose distinct 2 spots for the bars to be placed, each combo of 3 groups will be different, and all apples will add up to 18. We can also do this because the apples are indistinguishable. 20 \choose 2 is 190, therefore the answer is \boxed{\textbf{(C) }190}.

 

Solution 2 

Consider an unordered triple (a,b,c) where a+b+c=24 and a,b,c are not necessarily distinct. Then, we will either have 1, 3, or 6 distinguishable ways to assign a, b, and c to Alice, Becky, and Chris. Thus, our answer will be x+3y+6z for some nonnegative integers x,y,z. Notice that we only have 1 way to assign the numbers a,b,c to Alice, Becky, and Chris when a=b=c. As this only happens 1 way (a=b=c=8), our answer is 1+3y+6z for some y,z. Finally, notice that this implies the answer is 1 mod 3. The only answer choice that satisfies this is \boxed{\textbf{(C) }190}.

Link Problem
Related Paper
2022 AMC 8 2020 AMC 8 2018 AMC 8 2017 AMC 8
Table of Contents
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
Think Academy Powered by ChatGPT