2018 AMC 8
Complete problem set with solutions and individual problem pages
An amusement park has a collection of scale models, with a ratio of , of buildings and other sights from around the country. The height of the United States Capitol is feet. What is the height in feet of its duplicate to the nearest whole number?
- A.
- B.
- C.
- D.
- E.
Solution 1
You can see that since the ratio of real building's heights to the model building's height is . We also know that the U.S Capitol is feet in real life, so to find the height of the model, we divide by 20. That gives us which rounds to 14. Therefore, to the nearest whole number, the duplicate is .
Solution 2
We can compute and round our answer to get . It is basically Solution 1 without the ratio calculation. However, Solution 1 is referring further to the problem.
What is the value of the product
- A.
- B.
- C.
- D.
- E.
By adding up the numbers in each of the parentheses, we get:
.
Using telescoping, most of the terms cancel out diagonally. We are left with which is equivalent to . Thus, the answer would be .
Also, you can also make the fractions , which also yields
Students Arn, Bob, Cyd, Dan, Eve, and Fon are arranged in that order in a circle. They start counting: Arn first, then Bob, and so forth. When the number contains a 7 as a digit (such as 47) or is a multiple of 7 that person leaves the circle and the counting continues. Who is the last one present in the circle?
- A.
- B.
- C.
- D.
- E.
Solution 1
The five numbers which cause people to leave the circle are and
The most straightforward way to do this would be to draw out the circle with the people, and cross off people as you count.
Assuming the six people start with , Arn counts so he leaves first. Then, Cyd counts as there are numbers to be counted from this point. Then, Fon, Bob, and Eve, count, and , respectively, so the last one standing is Dan. Hence, the answer would be .
Solution 2
Assign each person a position: Arn is in position , Bob in , etc. Note that if there are people standing in a circle, a person will say a number that is congruent to their position modulo . It follows that if there are numbers to be said (with someone leaving on the ), the person that leaves will stand in position
The five numbers which cause people to leave the circle are and Since there are initially people in the circle, so the person who leaves stands in position , or position .
Arn now leaves, and because Bob is the next person to say a number, we reassign the positions such that Bob is in position , Cyd in , and Fon in . There are more numbers to be said, and someone leaves on the . It follows that the person who leaves stands in position .
Cyd leaves the circle, and people remain, namely Bob, Dan, Eve, and Fon. Assign the position numbers such that Dan has , Eve , etc. There are more numbers to be said, and someone leaves on the . The person standing in position (Fon) now leaves.
There are two people left, Eve and Dan, with Dan in position now. There are more numbers to be said, and Eve is standing in position , so she leaves.
The last person standing is .
The twelve-sided figure shown has been drawn on graph paper. What is the area of the figure in ?
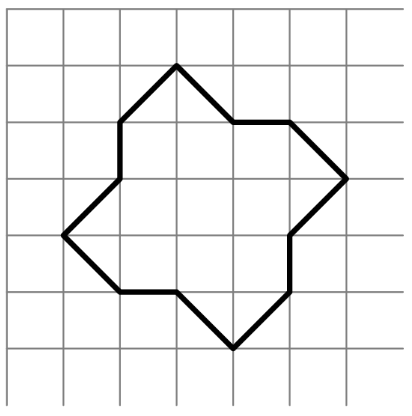
- A.
- B.
- C.
- D.
- E.
Solution 1
We count unit squares in the middle, and small triangles, which gives 4 rectangles each with an area of . Thus, the answer is .
Solution 2
We can see here that there are total squares in the middle. We also see that the triangles that make the corners of the shape have an area half the squares' area. Then, we can easily find that each corner has an area of one square and there are corners so we add that to the original 9 squares to get .
What is the value of ?
- A.
- B.
- C.
- D.
- E.
Solution 1
Rearranging the terms, we get , and our answer is .
Solution 2
We can see that the last numbers of each of the sets (even numbers and odd numbers) have a difference of two. So, do the second last ones and so on. Now, all we need to find is the number of integers in any of the sets (I chose even) to get .
On a trip to the beach, Anh traveled 50 miles on the highway and 10 miles on a coastal access road. He drove three times as fast on the highway as on the coastal road. If Anh spent 30 minutes driving on the coastal road, how many minutes did his entire trip take?
- A.
- B.
- C.
- D.
- E.
Solution 1
Since Anh spends half an hour to drive miles on the coastal road, his speed is . His speed on the highway then is . He drives miles, so he drives for hours, which is equal to minutes (Note that miles per hour is the same as mile per minute). The total amount of minutes spent on his trip is .
Solution 2
Since Anh drives times as fast on the highway, it takes him of the time to drive miles on the highway than on the coastal road. of is , and since he drives miles on the highway, we multiply by to get . This means it took him minutes to drive on the highway, and if we add the minutes it took for him to drive on the coastal road, we would get .
The -digit number is divisible by . What is the remainder when this number is divided by ?
- A.
- B.
- C.
- D.
- E.
We use the property that the digits of a number must sum to a multiple of if it are divisible by . This means must be divisible by . The only possible value for then must be . Since we are looking for the remainder when divided by , we can ignore the thousands. The remainder when is divided by is .
Mr. Garcia asked the members of his health class how many days last week they exercised for at least 30 minutes. The results are summarized in the following bar graph, where the heights of the bars represent the number of students.
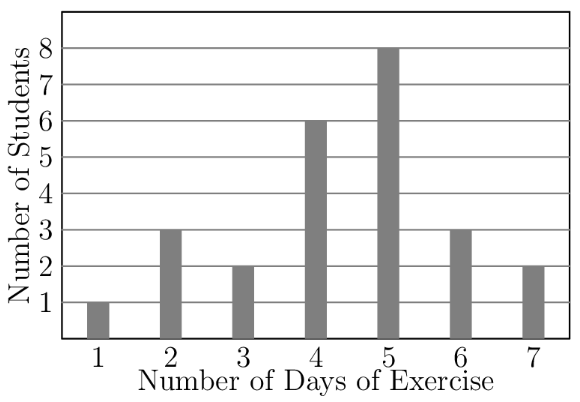
What was the mean number of days of exercise last week, rounded to the nearest hundredth, reported by the students in Mr. Garcia's class?
- A.
- B.
- C.
- D.
- E.
The mean, or average number of days is the total number of days divided by the total number of students. The total number of days is . The total number of students is . Hence, .
Monica is tiling the floor of her 12-foot by 16-foot living room. She plans to place one-foot by one-foot square tiles to form a border along the edges of the room and to fill in the rest of the floor with two-foot by two-foot square tiles. How many tiles will she use?
- A.
- B.
- C.
- D.
- E.
Solution 1
She will place tiles around the border. For the inner part of the room, we have square feet. Each tile takes up square feet, so he will use tiles for the inner part of the room. Thus, the answer is .
Solution 2
The area around the border: . The area of tiles around the border: . Therefore, is the number of tiles around the border.
The inner part will have . The area of those tiles are . is the amount of tiles for the inner part. So, .
The harmonic mean of a set of non-zero numbers is the reciprocal of the average of the reciprocals of the numbers. What is the harmonic mean of 1, 2, and 4?
- A.
- B.
- C.
- D.
- E.
The sum of the reciprocals is . Their average is . Taking the reciprocal of this gives .
Abby, Bridget, and four of their classmates will be seated in two rows of three for a group picture, as shown.
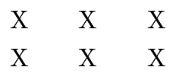
If the seating positions are assigned randomly, what is the probability that Abby and Bridget are adjacent to each other in the same row or the same column?
- A.
- B.
- C.
- D.
- E.
Solution 1
There are a total of ways to arrange the kids.
Abby and Bridget can sit in 3 ways if they are adjacent in the same column:
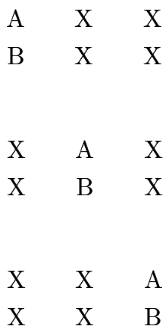
For each of these seat positions, Abby and Bridget can switch seats, and the other 4 people can be arranged in ways which results in a total of ways to arrange them.
By the same logic, there are 4 ways for Abby and Bridget to be placed if they are adjacent in the same row: they can swap seats, and the other people can be arranged in ways for a total of ways to arrange them.
We sum the 2 possibilities up to get or .
Solution 2
We can ignore other students, and treat Abby and Bridget as indistinguishable (since we only care about adjacency, not their order). Thus, the total number of ways is . In one row, they can be adjacent 2 ways: . In one column, they can only be adjacent 1 way: . Add these cases , and therefore, P(Abby and Bridget sitting adjacent) is .
The clock in Sri's car, which is not accurate, gains time at a constant rate. One day as he begins shopping, he notes that his car clock and his watch (which is accurate) both say noon. When he is done shopping, his watch says and his car clock says . Later that day, Sri loses his watch. He looks at his car clock and it says . What is the actual time?
- A.
- B.
- C.
- D.
- E.
Solution 1
We see that every minutes the clock passes, the watch passes minutes. That means that the clock is as fast the watch, so we can set up proportions. . Cross-multiplying we get . Now, this is obviously redundant, because we could just eyeball it to see that the watch would have passed hours. But this method is better when the numbers are a bit more complex, which makes it both easier and reliable. Either way, our answer is .
Solution 2
The ratio of the car clock to the watch clock is a ratio of 35:30 or 7:6 due to the clock being ahead by 5 minutes after 30 minutes has passed. This means that when the car clock passes hours, the watch has passed hours, meaning that the time would be .
Laila took five math tests, each worth a maximum of points. Laila's score on each test was an integer between and , inclusive. Laila received the same score on the first four tests, and she received a higher score on the last test. Her average score on the five tests was . How many values are possible for Laila's score on the last test?
- A.
- B.
- C.
- D.
- E.
Solution 1
Say Laila gets a value of on her first 4 tests, and a value of on her last test. Thus, .
Because and are different, must be less than and must be greater than . When decreases by , must increase by to keep the total constant.
The greatest value for is (as would make non-integer). In the range , only values for result in integer values for : 86, 90, 94 and 98. Thus, the answer is .
Solution 2
The average score is which leads us to suppose that Laila got all points for the tests. We know that Laila got the same points in the first four tests and they are all lower than the last test. Let the first four tests be points, then the last test must be points to keep the average fixed. Continue to decrement the first four tests to identify other possible combinations. The possible points for the fifth test are , , , . The answer is .
Let be the greatest five-digit number whose digits have a product of . What is the sum of the digits of ?
- A.
- B.
- C.
- D.
- E.
Solution 1
If we start off with the first digit, we know that it can't be since is not a factor of . We go down to the digit , which does work since it is a factor of . Now, we have to know what digits will take up the remaining four spots. To find this result, just divide . The next place can be , as it is the largest factor, aside from . Consequently, our next three values will be and if we use the same logic. Therefore, our five-digit number is , so the sum is .
Solution 2
is , so we have . (Alternatively, you could identify the prime factors .) Now look for the largest digit you can create by combining these factors.
Use this largest digit for the ten-thousands place: _ , _ _ _
Next you use the and the for the next places: _ _ (You can't use because the was used to make .)
Fill the remaining places with 1:
.
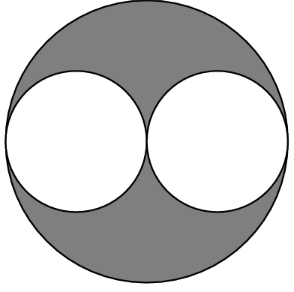
In the diagram below, a diameter of each of the two smaller circles is a radius of the larger circle. If the two smaller circles have a combined area of square unit, then what is the area of the shaded region, in square units?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let the radius of the large circle be . Then, the radius of the smaller circles are . The areas of the circles are directly proportional to the square of the radii, so the ratio of the area of the small circle to the large one is ( is of .) This means the combined area of the 2 smaller circles is half of the larger circle, and therefore the shaded region is equal to the combined area of the 2 smaller circles, which is .
Solution 2
Let the radius of the two smaller circles be . It follows that the area of one of the smaller circles is . Thus, the area of the two inner circles combined would evaluate to which is . Since the radius of the bigger circle is two times that of the smaller circles (the diameter), the radius of the larger circle in terms of would be . The area of the larger circle would come to .
Subtracting the area of the smaller circles from that of the larger circle (since that would be the shaded region), we have
Therefore, the area of the shaded region is .
Professor Chang has nine different language books lined up on a bookshelf: two Arabic, three German, and four Spanish. How many ways are there to arrange the nine books on the shelf keeping the Arabic books together and keeping the Spanish books together?
- A.
- B.
- C.
- D.
- E.
To solve this, treat the two Arabic books as one unit and the four Spanish books as another unit. Along with the three German books, you now have five units to arrange.
You can arrange these five units in ways. Within the Arabic block, the two books can be arranged in ways, and within the Spanish block, the four books can be arranged in ways.
Multiplying all these possibilities gives the total number of arrangements which is ways to arrange the nine books while keeping the Arabic and Spanish books together.
Bella begins to walk from her house toward her friend Ella's house. At the same time, Ella begins to ride her bicycle toward Bella's house. They each maintain a constant speed, and Ella rides times as fast as Bella walks. The distance between their houses is miles, which is feet, and Bella covers feet with each step. How many steps will Bella take by the time she meets Ella?
- A.
- B.
- C.
- D.
- E.
Solution 1
Every 10 feet Bella goes, Ella goes 50 feet, which means a total of 60 feet. They need to travel that 60 feet times to travel the entire 2 miles. Since Bella goes 10 feet 176 times, this means that she travels a total of 1760 feet. And since she walks 2.5 feet each step,
Solution 2
We can turn into an improper fraction. It will then become . Since Ella bikes 5 times faster, we multiply . Then we add to find the distance they walk and bike together for each step of Bella's: . This means that they travel 15 ft. of distance for each step that Bella takes. Divide 10,560 by 15 to find that Bella takes steps.
How many positive factors does have?
- A.
- B.
- C.
- D.
- E.
Solution 1
We can first find the prime factorization of , which is . Now, we add one to our powers and multiply. Therefore, the answer is
Note: 23232 is a large number, so we can look for shortcuts to factor it. One way to factor it quickly is to use 3 and 11 divisibility rules to observe that .
Another way is to spot the "32" and compute that .
A third way to factor it is to observe . Factoring out the gives us . Since and , we have .
Solution 2
Observe that = , so this is of which is , which has factors. The answer is .
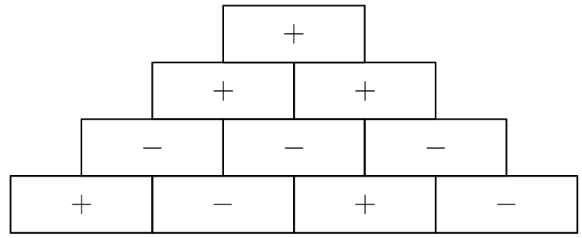
In a sign pyramid a cell gets a "+" if the two cells below it have the same sign, and it gets a "-" if the two cells below it have different signs. The diagram below illustrates a sign pyramid with four levels. How many possible ways are there to fill the four cells in the bottom row to produce a "+" at the top of the pyramid?
- A.
- B.
- C.
- D.
- E.
Solution 1
You could just make out all of the patterns that make the top positive. In this case, you would have the following patterns:
+−−+, −++−, −−−−, ++++, −+−+, +−+−, ++−−, −−++. There are 8 patterns and so the answer is .
Solution 2
The top box is fixed by the problem.
Choose the left 3 bottom-row boxes freely. There are ways.
Then the left 2 boxes on the row above are determined.
Then the left 1 box on the row above that is determined
Then the right 1 box on that row is determined.
Then the right 1 box on the row below is determined.
Then the right 1 box on the bottom row is determined, completing the diagram.
So the answer is .
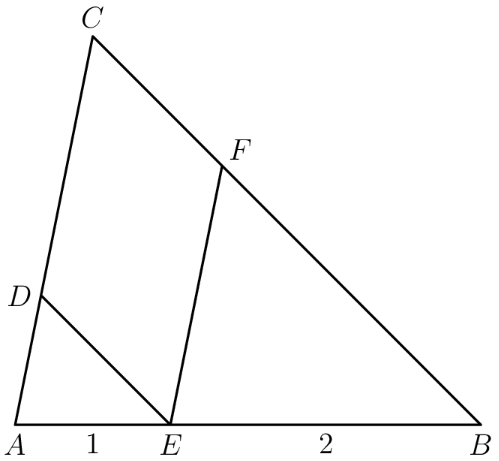
In a point is on with and Point is on so that and point is on so that What is the ratio of the area of to the area of
- A.
- B.
- C.
- D.
- E.
By similar triangles, we have . Similarly, we see that . Using this information, we get
Then, since , it follows that the . Thus, the answer would be .
How many positive three-digit integers have a remainder of when divided by , a remainder of when divided by , and a remainder of when divided by ?
- A.
- B.
- C.
- D.
- E.
Solution 1
Looking at the values, we notice that , and . This means we are looking for a value that is four less than a multiple of , , and . The least common multiple of these numbers is , so the numbers that fulfill this can be written as , where is a positive integer. This value is only a three-digit integer when is or , which gives and respectively. Thus, we have values, so our answer is .
Solution 2
Let us create the equations: , and we know , it gives us , which is the range of the value of z. Because of , then , so must be a multiple of 6. Because of , then , so must also be a multiple of . Hence, the value of must be a common multiple of and , which means multiples of . So, let's say ; then, , so . Thus, the answer is .
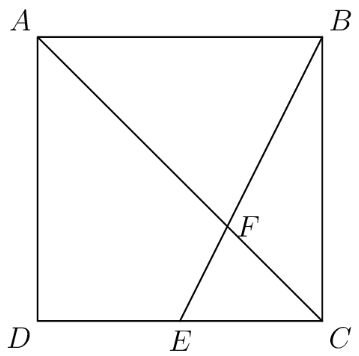
Point is the midpoint of side in square and meets diagonal at The area of quadrilateral is What is the area of
- A.
- B.
- C.
- D.
- E.
Solution 1
We can use analytic geometry for this problem.
Let us start by giving the coordinate , the coordinate , and so forth. and can be represented by the equations and , respectively. Solving for their intersection gives point coordinates .
Now, we can see that 's area is simply or . This means that pentagon 's area is of the entire square, and it follows that quadrilateral 's area is of the square.
The area of the square is then .
Solution 2
has half the area of the square. has base equal to half the square side length, and by AA Similarity with , it has the height, so has th of the area of square(). Thus, the area of the quadrilateral is of the area of the square. The area of the square is then .
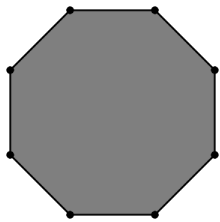
From a regular octagon, a triangle is formed by connecting three randomly chosen vertices of the octagon. What is the probability that at least one of the sides of the triangle is also a side of the octagon?
- A.
- B.
- C.
- D.
- E.
Solution 1
Choose side "lengths" for the triangle, where "length" is how many vertices of the octagon are skipped between vertices of the triangle, starting from the shortest side, and going clockwise, and choosing if the triangle is isosceles: , where either [ and ] or [ (but this is impossible in an octagon)].
Options are: with in { 0,5 ; 1,4 ; 2,3 ; 3,2 ; 4,1 }, and with { 1,3 ; 2,2}. of these have a side with length 1, which corresponds to an edge of the octagon. So, our answer is
Solution 2
We will use constructive counting to solve this. There are cases: Either all points are adjacent, or exactly points are adjacent.
If all points are adjacent, then we have choices. If we have exactly adjacent points, then we will have places to put the adjacent points and places to put the remaining point, so we have choices. The total amount of choices is .
Thus, our answer is .
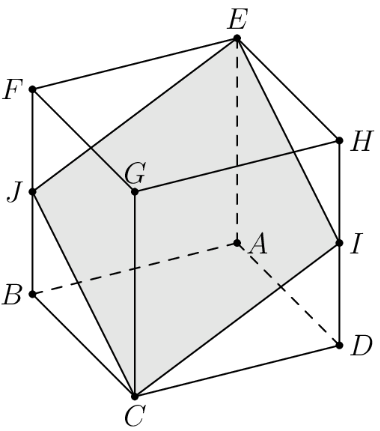
In the cube with opposite vertices and and are the midpoints of segments and respectively. Let be the ratio of the area of the cross-section to the area of one of the faces of the cube. What is
- A.
- B.
- C.
- D.
- E.
Solution 1
Note that is a rhombus by symmetry. Let the side length of the cube be . By the Pythagorean theorem, and . Since the area of a rhombus is half the product of its diagonals, the area of the cross section is . This gives . Thus, .
Solution 2
If the edges of the cube have same lengths , is the origin, is the positive direction, is the positive direction, and is the positive direction. Therefore, we have and . Hence, we can figure out that:
Note that is a rhombus, so . Finally, we can see that the answer is
How many perfect cubes lie between and , inclusive?
- A.
- B.
- C.
- D.
- E.
Solution 1
We compute . We're all familiar with what is, namely , which is too small. The smallest cube greater than it is . is too large to calculate, but we notice that , which therefore will clearly be the largest cube less than . So, the required number of cubes is .
Solution 2
First, . Then, . Now, we can see how many perfect cubes are between these two parameters. By guessing and checking, we find that it starts from and ends with . Now, by counting how many numbers are between these, we find the answer to be .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
