2017 AMC 8
Complete problem set with solutions and individual problem pages
Which of the following values is largest?
- A.
- B.
- C.
- D.
- E.
Solution 1
We will compute each expression.
A)
B)
C)
D)
E)
Ordering these, we get . Out of these, is the largest number and option adds up to . Therefore, the answer is .
Solution 2
We immediately see that every one of the choices, except for A and D, has a number multiplied by . This will only make the expression's value smaller. We are left with A and D, but in D, is multiplied by to get , whereas in answer choice A, we get out of and , instead of . Therefore, is your answer.
Alicia, Brenda, and Colby were the candidates in a recent election for student president. The pie chart below shows how the votes were distributed among the three candidates. If Brenda received votes, then how many votes were cast all together?
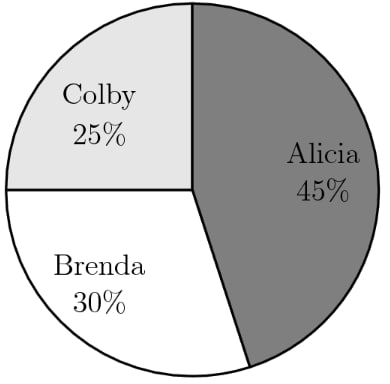
- A.
- B.
- C.
- D.
- E.
Solution 1
Let be the total amount of votes casted. From the chart, Brenda received of the votes and had votes. We can express this relationship as . Solving for , we get
Solution 2
We're being asked for the total number of votes cast -- that represents of the total number of votes. Brenda received votes, which is of the total number of votes. Multiplying by we get the total number of votes, which is
What is the value of the expression ?
- A.
- B.
- C.
- D.
- E.
= = = = = .
When is multiplied by the product is closest to which of the following?
- A.
- B.
- C.
- D.
- E.
We can approximate to and to Multiplying the two yields Thus, it shows our answer is
What is the value of the expression ?
- A.
- B.
- C.
- D.
- E.
Solution 1
It is well known that the sum of all numbers from to is . Therefore, the denominator is equal to . Now, we can cancel the factors of , , and from both the numerator and denominator, only leaving . This evaluates to .
Solution 2
First, we evaluate to get . We notice that is squared, so we can factor the denominator like then cancel the 6s out to get . Now that we have escaped fraction form, we multiply . Multiplying these, we get .
If the degree measures of the angles of a triangle are in the ratio , what is the degree measure of the largest angle of the triangle?
- A.
- B.
- C.
- D.
- E.
Solution 1
The sum of the ratios is . Since the sum of the angles of a triangle is , the ratio can be scaled up to The numbers in the ratio represent the angles of the triangle. The question asks for the largest, so the answer is .
Solution 2
We can denote the angles of the triangle as , , . Due to the sum of the angles in a triangle, . The greatest angle is and after substitution we get .
Let be a -digit positive integer, such as , whose first three digits are the same as its last three digits taken in the same order. Which of the following numbers must also be a factor of ?
- A.
- B.
- C.
- D.
- E.
Solution 1
To check, if a number is divisible by , take its unit digit and multiply it by , then add the result to the rest of the number, and repeat this step until the number is reduced to two digits. If the result is divisible by 19, then the original number is also divisible by .
After we got eliminated, we can see that the other options have a lot of 's in them. The divisibility rule for is add alternating digits up, then take the difference of them. The example number works like that. If we add variables, to make number , we can see that . Which is divisible by , so our answer choice is .
Solution 2
We are given one of the numbers that can represent , so we can just try out the options to see which one is a factor of . By the previous solution, 19 does not work even though it is a factor of the example number. We get .
Malcolm wants to visit Isabella after school today and knows the street where she lives but doesn't know her house number. She tells him, "My house number has two digits, and exactly three of the following four statements about it are true."
() It is prime.
() It is even.
() It is divisible by .
() One of its digits is .
This information allows Malcolm to determine Isabella's house number. What is its units digit?
- A.
- B.
- C.
- D.
- E.
Notice that () cannot be true. Otherwise, the number would have to be prime and be either even or divisible by . This only happens if the number is or , neither of which are two-digit numbers, so we run into a contradiction. Thus, we must have (), (), and () be true. By (), the -digit number is even, and thus, the digit in the tens place must be . The only even -digit number starting with and divisible by is , which has a units digit of
All of Marcy's marbles are blue, red, green, or yellow. One third of her marbles are blue, one fourth of them are red, and six of them are green. What is the smallest number of yellow marbles that Marcy could have?
- A.
- B.
- C.
- D.
- E.
Solution 1
The green marbles and yellow marbles form of the total marbles. Now, suppose the total number of marbles is . We know the number of yellow marbles is and a positive integer. Therefore, must divide . Trying the smallest multiples of for , we see that when , we get there are yellow marbles, which is impossible. However when , there are yellow marbles, which must be the smallest possible.
Solution 2
Since of the marbles are blue and are red, it is clear that the total number of marbles must be divisible by . If there are marbles, then are blue, are red, and are green, meaning that there are yellow marbles. This is impossible. Trying the next multiple of , , we find that are green, are red, and are green, meaning that the minimum number of yellow marbles is .
A box contains five cards, numbered , , , , and . Three cards are selected randomly without replacement from the box. What is the probability that is the largest value selected?
- A.
- B.
- C.
- D.
- E.
Solution 1
There are possible groups of cards that can be selected. If is the largest card selected, then the other two cards must be either , , or , for a total groups of cards. Then, the probability is just .
Solution 2
P (no )= = . This is the fraction of total cases with no fives. p (no and no )= = = . This is the intersection of no fours and no fives. Subtract the fraction of no fours and no fives from that of no fives. .
A square-shaped floor is covered with congruent square tiles. If the total number of tiles that lie on the two diagonals is , how many tiles cover the floor?
- A.
- B.
- C.
- D.
- E.
Solution 1
Since the number of tiles lying on both diagonals is , counting one tile twice, there are tiles on each side, where x is the number of tiles on the side length of the square. This is because the number of tiles on the square's diagonal is equal to the number of tiles on the square's side length.Therefore, our answer is .
Solution 2
Visualize it as 4 separate diagonals connecting to one square in the middle. Each square on the diagonal corresponds to one square of horizontal/vertical distance (because it's a square). So, we figure out the length of each separate diagonal, multiply by two, and then add 1. (Realize that we can just join two of the separate diagonals on opposite sides together to save some time in calculations.) Therefore, the edge length is:
Thus, our solution is .
The smallest positive integer greater than that leaves a remainder of when divided by , , and lies between which of the following pairs of numbers?
- A.
- B.
- C.
- D.
- E.
Solution 1
Since the remainder is the same for all numbers, then we will only need to find the lowest common multiple of the three given numbers, and add the given remainder. The is . Since , that is in the range of
Solution 2
Call the number we want to find . We can say that
We can also say that is divisible by , and Therefore, , so which is in the range of
Peter, Emma, and Kyler played chess with each other. Peter won games and lost games. Emma won games and lost games. If Kyler lost games, how many games did he win?
- A.
- B.
- C.
- D.
- E.
Given games, there must be a total of wins and losses. Hence, where is Kyler's wins. , so our final answer is
Chloe and Zoe are both students in Ms. Demeanor's math class. Last night, they each solved half of the problems in their homework assignment alone and then solved the other half together. Chloe had correct answers to only of the problems she solved alone, but overall of her answers were correct. Zoe had correct answers to of the problems she solved alone. What was Zoe's overall percentage of correct answers?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let the number of questions that they solved alone be . Let the percentage of problems they correctly solve together be %. As given,
.
Hence, .
Zoe got problems right out of . Therefore, Zoe got percent of the problems correct.
Solution 2
Assume the total amount of problems is per half homework assignment since we are dealing with percentages, not values. Then, we know that Chloe got problems correct by herself and got problems correct overall. We also know that Zoe had problems she did correctly alone. We can see that the total amount of correct problems Chloe and Zoe did together was . Therefore, Zoe did problems out of problems correctly. This is percent.
In the arrangement of letters and numerals below, by how many different paths can one spell AMC8? Beginning at the A in the middle, a path only allows moves from one letter to an adjacent (above, below, left, or right, but not diagonal) letter. One example of such a path is traced in the picture.
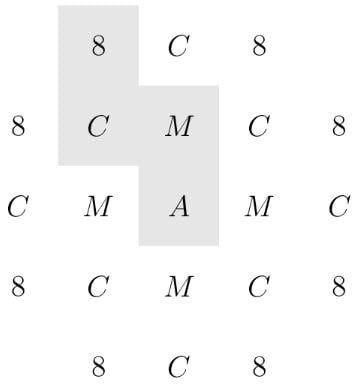
- A.
- B.
- C.
- D.
- E.
Solution 1
Notice that the is adjacent to s, each is adjacent to s, and each is adjacent to 's. So for each , there are s, and for each , there are s, and for each , there are s. Thus, the answer is
Solution 2
There are three different kinds of paths that are on this diagram. The first kind is when you directly count , , in a straight line. The second is when you count , turn left or right to get , then go up or down to count and . The third is the one where you start with , move up or down to count , turn left or right to count , then move straight again to get .
There are paths for each kind of path, making for paths.
In the figure below, choose point on so that and have equal perimeters. What is the area of ?
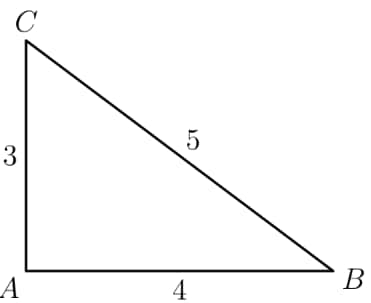
- A.
- B.
- C.
- D.
- E.
Solution 1
We know that the perimeters of the two small triangles are and . Setting both equal and using , we have and . Now, we simply have to find the area of . Since , we must have . Combining this with the fact that , we get .
Solution 2
Since is less than , must be more than to equate the perimeter. Hence, , so . Therefore, the area of is
Starting with some gold coins and some empty treasure chests, I tried to put gold coins in each treasure chest, but that left treasure chests empty. So instead I put gold coins in each treasure chest, but then I had gold coins left over. How many gold coins did I have?
- A.
- B.
- C.
- D.
- E.
Solution 1
We can represent the amount of gold with and the amount of chests with . We can use the problem to make the following equations:
We do this because for chests there are empty and if were in each multiplied by is left.
Therefore, This implies that We therefore have So, our answer is .
Solution 2
With coins, there are chests, by the first condition. These don't fit in with the second condition, so we move onto coins. By the same first condition, there are chests(). This also doesn't fit with the second condition. So, onto coins. The first condition implies that there are chests, which DOES fit with the second condition, since . Thus, the desired value is .
In the non-convex quadrilateral shown below, is a right angle, , , , and . What is the area of quadrilateral ?
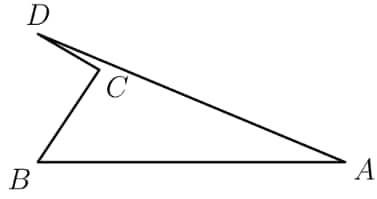
- A.
- B.
- C.
- D.
- E.
Solution 1
We first connect point with point .
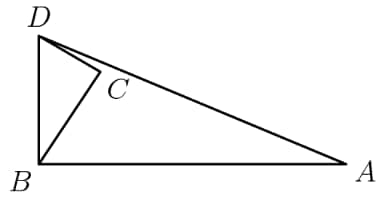
We can see that is a right triangle. We can also see that is a right triangle, by the Pythagorean triple. With these lengths, we can solve the problem. The area of is , and the area of is . Thus, the area of quadrilateral is
Solution 2
is a right triangle. So the area of is . Then we can use Heron's formula to compute the area of whose sides have lengths , , and . The area of = , where s is the semi-perimeter of the triangle, that is Thus, the area of is , so the area of is
For any positive integer , the notation denotes the product of the integers through . What is the largest integer for which is a factor of the sum ?
- A.
- B.
- C.
- D.
- E.
Factoring out , we have , which is . Next, has factors of . The is because of all the multiples of .The is because of all the multiples of . Now, has factors of , so there are a total of factors of .
An integer between and , inclusive, is chosen at random. What is the probability that it is an odd integer whose digits are all distinct?
- A.
- B.
- C.
- D.
- E.
There are options for the last digit as the integer must be odd. The first digit now has options left (it can't be or the same as the last digit). The second digit also has options left (it can't be the same as the first or last digit). Finally, the third digit has options (it can't be the same as the three digits that are already chosen).
Since there are total integers, our answer is
Suppose , , and are nonzero real numbers, and . What are the possible value(s) for ?
- A.
- B.
- C.
- D.
- E.
There are cases to consider:
Case : of , , and are positive and the other is negative. Without loss of generality (WLOG), we can assume that and are positive and is negative. In this case, we have that
Case : of , , and are negative and the other is positive. WLOG, we can assume that and are negative and is positive. In this case, we have that
Note these are the only valid cases, for neither negatives nor positives would work as they cannot sum up to . In both cases, we get that the given expression equals .
In the right triangle , , , and angle is a right angle. A semicircle is inscribed in the triangle as shown. What is the radius of the semicircle?
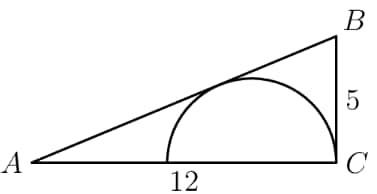
- A.
- B.
- C.
- D.
- E.
Solution 1
We can draw another radius from the center to the point of tangency. This angle, , is . Label the center , the point of tangency , and the radius .
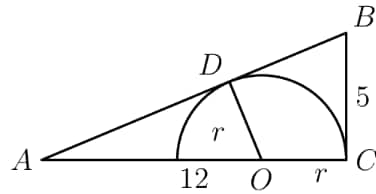
Since is a kite, then . Also, . By the Pythagorean Theorem, . Solving, .
Solution 2
If we reflect triangle over line , we will get isosceles triangle . By the Pythagorean Theorem, we are capable of finding out that the . Hence, . Therefore, as of triangle , the radius of its inscribed circle
Each day for four days, Linda traveled for one hour at a speed that resulted in her traveling one mile in an integer number of minutes. Each day after the first, her speed decreased so that the number of minutes to travel one mile increased by minutes over the preceding day. Each of the four days, her distance traveled was also an integer number of miles. What was the total number of miles for the four trips?
- A.
- B.
- C.
- D.
- E.
It is well known that . In the question, we want distance. From the question, we have that the time is minutes or hour. By the equation derived from , we have , so the speed is mile per minutes. Because we want the distance, we multiply the time and speed together yielding . The minutes cancel out, so now we have as our distance for the first day. The distance for the following days are:
We know that are all factors of , therefore, because the factors have to be in an arithmetic sequence with the common difference being and is the only solution.
Mrs. Sanders has three grandchildren, who call her regularly. One calls her every three days, one calls her every four days, and one calls her every five days. All three called her on December , . On how many days during the next year did she not receive a phone call from any of her grandchildren?
- A.
- B.
- C.
- D.
- E.
Solution 1
We use Principle of Inclusion-Exclusion. There are days in the year, and we subtract the days that she gets at least phone call, which is
To this result we add the number of days where she gets at least phone calls in a day because we double subtracted these days, which is
We now subtract the number of days where she gets three phone calls, which is Therefore, our answer is
Solution 2
Note that so there is a cycle every days.
As shown below, all days in a cycle that Mrs. Sanders receives a phone call from any of her grandchildren are colored in red, yellow, or green.
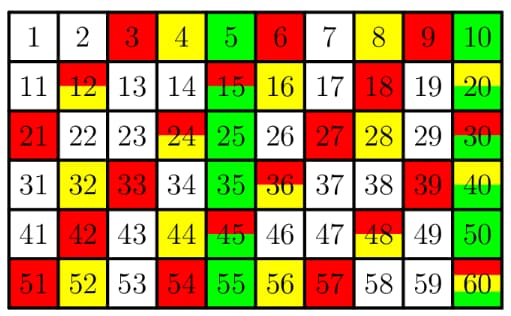
The year has days, or cycles and days.
- For each cycle, there are days that Mrs. Sanders does not receive a phone call, as indicated by the white squares.
- For the last days, there are days that Mrs. Sanders does not receive a phone call, as indicated by the first days in a cycle. Together, the answer is
In the figure shown, and are line segments each of length , and . Arcs and are each one-sixth of a circle with radius . What is the area of the region shown?
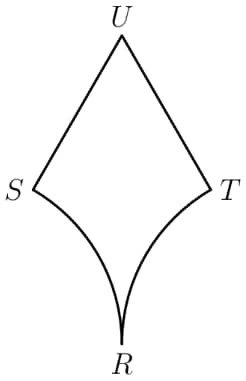
- A.
- B.
- C.
- D.
- E.
Solution 1

In addition to the given diagram, we can draw lines and The area of rhombus is half the product of its diagonals, which is . However, we have to subtract off the circular segments. The area of those can be found by computing the area of the circle with radius , multiplying it by , then finally subtracting the area of an equilateral triangle with a side length from the sector. The sum of the areas of the circular segments is The area of rhombus minus the circular segments is
Solution 2
We can extend , to and , respectively, such that and are collinear to point . Connect . We can see points , are probably circle centers of arc , , respectively. So, . Thus, is equilateral. The area of is , or , and both one sixth circles total up to . Finally, the answer is .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
