2015 AMC 8
Complete problem set with solutions and individual problem pages
Onkon wants to cover his room's floor with his favourite red carpet. How many square yards of red carpet are required to cover a rectangular floor that is feet long and feet wide? (There are 3 feet in a yard.)
- A.
- B.
- C.
- D.
- E.
Solution 1
We need square feet of carpet to cover the floor. Since there are square feet in a square yard, we divide this by to get square yards.
Solution 2
Since there are feet in a yard, we divide by to get yards, and by to get yards. To find the area of the carpet, we then multiply these two values together to get square yards.
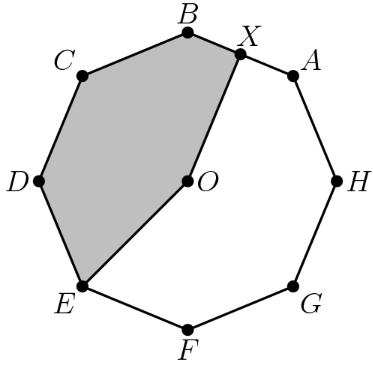
Point is the center of the regular octagon , and is the midpoint of the side What fraction of the area of the octagon is shaded?
- A.
- B.
- C.
- D.
- E.
Solution 1
Since octagon is a regular octagon, it is split into equal parts, such as triangles , etc. These parts, since they are all equal, are of the octagon each. The shaded region consists of of these equal parts plus half of another, so the fraction of the octagon that is shaded is
Solution 2
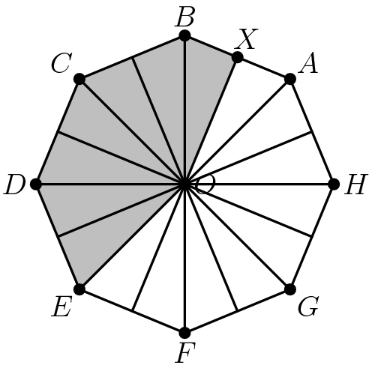
The octagon has been divided up into identical triangles (and thus they each have equal area). Since the shaded region occupies out of the total triangles, the answer is .
Jack and Jill are going swimming at a pool that is one mile from their house. They leave home simultaneously. Jill rides her bicycle to the pool at a constant speed of miles per hour. Jack walks to the pool at a constant speed of miles per hour. How many minutes before Jack does Jill arrive?
- A.
- B.
- C.
- D.
- E.
Using , we can set up an equation for when Jill arrives at the swimming pool:
Solving for , we get that Jill gets to the pool in of an hour, which is minutes. Doing the same for Jack, we get that
Jack arrives at the pool in of an hour, which in turn is minutes. Thus, Jill has to wait
The Blue Bird High School chess team consists of two boys and three girls. A photographer wants to take a picture of the team to appear in the local newspaper. She decides to have them sit in a row with a boy at each end and the three girls in the middle. How many such arrangements are possible?
- A.
- B.
- C.
- D.
- E.
There are ways to order the boys on the ends, and there are ways to order the girls in the middle. We get the answer to be .
Billy's basketball team scored the following points over the course of the first games of the season. If his team scores in the game, which of the following statistics will show an increase?
- A.
- B.
- C.
- D.
- E.
Solution 1
When they score a on the next game, the range increases from to . This means the increased.
Note: The range is defined to be the difference of the largest element and the smallest element of a set.
Solution 2
Because is less than the score of every game they've played so far, the measures of center will never rise. Only measures of spread, such as the , may increase.
In , , and . What is the area of ?
- A.
- B.
- C.
- D.
- E.
Solution 1
We know the semi-perimeter of is . Next, we use Heron's Formula to find that the area of the triangle is just .
Solution 2
Splitting the isosceles triangle in half, we get a right triangle with hypotenuse and leg . Using the Pythagorean Theorem , we know the height is . Now that we know the height, the area is .
Each of two boxes contains three chips numbered , , . A chip is drawn randomly from each box and the numbers on the two chips are multiplied. What is the probability that their product is even?
- A.
- B.
- C.
- D.
- E.
Solution 1
You can make this problem into a spinner problem. You have the first spinner with equally divided
sections: , and . You make a second spinner that is identical to the first, with equal sections of
,, and . If the first spinner lands on , it must land on two for the result to be even. You write down the first
combination of numbers: . Next, if the spinner lands on , it can land on any number on the second
spinner. We now have the combinations of and . Finally, if the first spinner ends on , we
have Since there are possible combinations, and we have evens, the final answer is
.
Solution 2
We can list out the numbers. Box A has chips , , and , and Box B also has chips , , and . Chip (from Box A)
could be with 3 partners from Box B. This is also the same for chips and from Box A. total sums. Chip could be multiplied with 2 other chips to make an even product, just like chip . Chip can only multiply with 1 chip. . The answer is .
What is the smallest whole number larger than the perimeter of any triangle with a side of length and a side of length ?
- A.
- B.
- C.
- D.
- E.
Solution 1
We know from the Triangle Inequality that the last side, , fulfills . Adding to both sides of the inequality, we get , and because is the perimeter of our triangle, is our answer.
Solution 2
, fulfills , meaning that s<24. The greatest value of s can be 23. 23+5+19 is 47. 48 is our nearest answer choice so its .
On her first day of work, Janabel sold one widget. On day two, she sold three widgets. On day three, she sold five widgets, and on each succeeding day, she sold two more widgets than she had sold on the previous day. How many widgets in total had Janabel sold after working days?
- A.
- B.
- C.
- D.
- E.
Solution 1
First, we have to find how many widgets she makes on Day . We can write the linear equation to represent this situation. Then, we can plug in for : -- -- . The sum of is .
Solution 2
The sum is just the first odd counting/natural numbers, which is .
How many integers between and have four distinct digits?
- A.
- B.
- C.
- D.
- E.
There are choices for the first number, since it cannot be , there are only choices left for the second number since it must differ from the first, choices for the third number, since it must differ from the first two, and choices for the fourth number, since it must differ from all three. This means there are integers between and with four distinct digits.
In the small country of Mathland, all automobile license plates have four symbols. The first must be a vowel (A, E, I, O, or U), the second and third must be two different letters among the 21 non-vowels, and the fourth must be a digit (0 through 9). If the symbols are chosen at random subject to these conditions, what is the probability that the plate will read "AMC8"?
- A.
- B.
- C.
- D.
- E.
Solution 1
There is one favorable case, which is the license plate says "AMC8." We must now find how many total cases there are. There are choices for the first letter (since it must be a vowel), choices for the second letter (since it must be of consonants), choices for the third letter (since it must differ from the second letter), and choices for the digit. This leads to total possible license plates. Therefore, the probability of a license plate saying "AMC8" is .
Solution 2
The probability of choosing A as the first letter is . The probability of choosing next is . The probability of choosing C as the third letter is (since there are other consonants to choose from other than M). The probability of having as the last number is . We multiply all these to obtain .
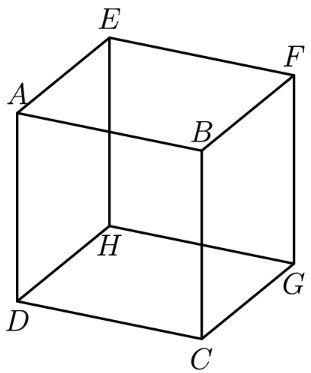
How many pairs of parallel edges, such as and or and , does a cube have?
- A.
- B.
- C.
- D.
- E.
Solution 1
We first count the number of pairs of parallel lines that are in the same direction as . The pairs of parallel lines are , , , , , and . These are pairs total. We can do the same for the lines in the same direction as and . This means there are total pairs of parallel lines.
Solution 2
Look at any edge, let's say . There are three ways we can pair with another edge. , , and . There are 12 edges on a cube. 3 times 12 is 36. We have to divide by 2 because every pair is counted twice, so is total pairs of parallel lines.
How many subsets of two elements can be removed from the set so that the mean (average) of the remaining numbers is ?
- A.
- B.
- C.
- D.
- E.
Solution 1
Since there will be elements after removal, and their mean is , we know their sum is . We also know that the sum of the set pre-removal is . Thus, the sum of the elements removed is . There are only subsets of elements that sum to : .
Solution 2
We can simply remove subsets of numbers while leaving only behind. The average of this one-number set is still , so the answer is .
Which of the following integers cannot be written as the sum of four consecutive odd integers?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let our numbers be , where is odd. Then, our sum is . The only answer choice that cannot be written as , where is odd, is .
Solution 2
If the four consecutive odd integers are and ; then, the sum is . All the integers are divisible by except .
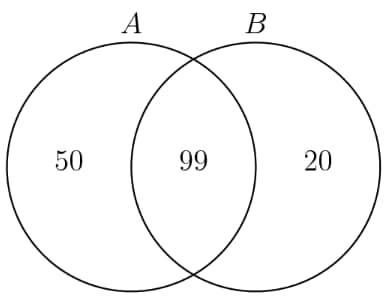
At Euler Middle School, students voted on two issues in a school referendum with the following results: voted in favor of the first issue and voted in favor of the second issue. If there were exactly students who voted against both issues, how many students voted in favor of both issues?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let:
- be the number of students who voted in favor of the first issue,
- be the number of students who voted in favor of the second issue,
- be the number of students who voted in favor of both issues.
We are given:
-
-
- students voted against both issues, so the number of students who voted for at least one issue is:
By the principle of inclusion and exclusion:
Substitute known values:
Solution 2
We can see that this is a Venn Diagram Problem.
First, we analyze the information given. There are students. Let's use A as the first issue and B as the second issue.
students were for A, and students were for B. There were also students against both A and B.
Solving this without a Venn Diagram, we subtract away from the total, . Out of the remaining , we have people for A and
people for B. We add this up to get . Since that is more than what we need, we subtract from to get
.
In a middle-school mentoring program, a number of the sixth graders are paired with a ninth-grade student as a buddy. No ninth grader is assigned more than one sixth-grade buddy. If of all the ninth graders are paired with of all the sixth graders, what fraction of the total number of sixth and ninth graders have a buddy?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let the number of sixth graders be , and the number of ninth graders be . Thus, , which simplifies to . Since we are trying to find the value of , we can just substitute for into the equation. We then get a value of .
Solution 2
We see that the minimum number of ninth graders is , because if there are then there is ninth-grader with a buddy, which would mean there are sixth graders, which is impossible (of course unless you really do have half of a person). With ninth-graders, of them are in the buddy program, so there sixth-graders total, two of whom have a buddy. Thus, the desired fraction is .
Jeremy's father drives him to school in rush hour traffic in 20 minutes. One day there is no traffic, so his father can drive him 18 miles per hour faster and gets him to school in 12 minutes. How far in miles is it to school?
- A.
- B.
- C.
- D.
- E.
Solution 1
For starters, we identify d as distance and v as velocity (speed)
Writing the equation gives us: and .
This gives , which gives , which then gives .
Solution 2
d = rtd=times r = times (r + 18)$
so , plug into the first one and it's miles to school.
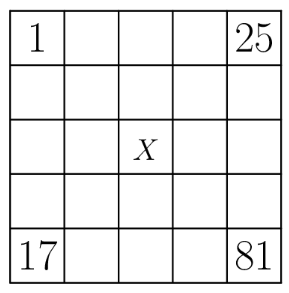
An arithmetic sequence is a sequence in which each term after the first is obtained by adding a constant to the previous term. For example, is an arithmetic sequence with five terms, in which the first term is and the constant added is . Each row and each column in this array is an arithmetic sequence with five terms. The square in the center is labelled as shown. What is the value of ?
- A.
- B.
- C.
- D.
- E.
Solution 1
We begin filling in the table. The top row has a first term and a fifth term , so we have the common difference is . This means we can fill in the first row of the table:
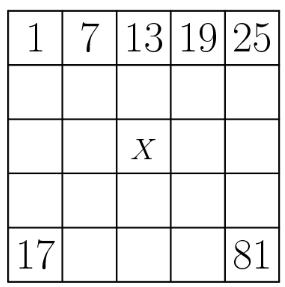
The fifth row has a first term of and a fifth term of , so the common difference is . We can fill in the fifth row of the table as shown:
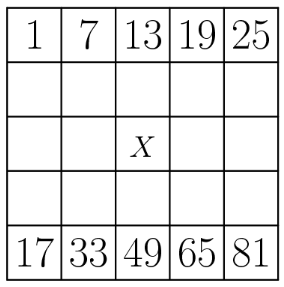
We must find the third term of the arithmetic sequence with a first term of and a fifth term of . The common difference of this sequence is , so the third term is .
Solution 2
The middle term of the first row is , since the middle number is just the average in an arithmetic sequence. Similarly, the middle of the bottom row is . Applying this again for the middle column, the answer is .
A triangle with vertices as , , and is plotted on a grid. What fraction of the grid is covered by the triangle?

- A.
- B.
- C.
- D.
- E.
Solution 1
The area of is equal to half the product of its base and height. By the Pythagorean Theorem, we find its height is , and its base is . We multiply these and divide by to find the area of the triangle is . Since the grid has an area of , the fraction of the grid covered by the triangle is .
Solution 2
Note angle is right; thus, the area is ; thus, the fraction of the total is .
Ralph went to the store and bought pairs of socks for a total of . Some of the socks he bought cost a pair, some of the socks he bought cost a pair, and some of the socks he bought cost a pair. If he bought at least one pair of each type, how many pairs of socks did Ralph buy?
- A.
- B.
- C.
- D.
- E.
Solution 1
So, let there be pairs of socks, pairs of socks, and pairs of socks.
We have , , and .
Now, we subtract to find , and . It follows that is a multiple of and is a multiple of . Since sum of 2 multiples of 3 = multiple of 3, so we must have .
Therefore, , and it follows that . Now, , as desired.
Solution 2
Since the total cost of the socks was and Ralph bought pairs, the average cost of each pair of socks is .
There are two ways to make packages of socks that average to . You can have:
Two pairs and one pair (package adds up to )
One pair and one pair (package adds up to )
Now, we need to solve
where is the number of packages and is the number of packages. We see our only solution (that has at least one of each pair of sock) is , which yields the answer of .
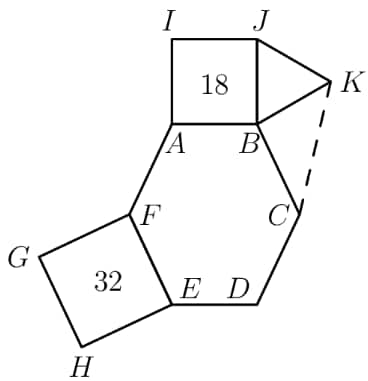
In the given figure, hexagon is equiangular, and are squares with areas and respectively, is equilateral and . What is the area of ?
- A.
- B.
- C.
- D.
- E.
Solution 1
Clearly, since is a side of a square with area , . Now, since , we have .
We know that is a side of a square with area , so . Since is equilateral, .
Lastly, is a right triangle. We see that , so is a right triangle with legs and . Now, its area is .
Solution 2
Since , and , . Meanwhile, , and since is equilateral, . If is equiangular, , where is the number of sides of the shape. Adding all the angles around gives , so . Because is right, the area of . Therefore, the answer is .
On June 1, a group of students is standing in rows, with 15 students in each row. On June 2, the same group is standing with all of the students in one long row. On June 3, the same group is standing with just one student in each row. On June 4, the same group is standing with 6 students in each row. This process continues through June 12 with a different number of students per row each day. However, on June 13, they cannot find a new way of organizing the students. What is the smallest possible number of students in the group?
- A.
- B.
- C.
- D.
- E.
Solution 1
Since we know the number must be a multiple of , we can eliminate . We also know that after days, the students can't find any more arrangements, meaning the number has factors. Now, we just list the factors of every number, starting with :
has factors, so the answer is .
Solution 2
We know that the number of students in the group has to be a multiple of 15, so we can eliminate A. However, on June 13, they cannot find a new way of organizing the students meaning that the number has only 12 factors. The prime factorization of 60 is equal to 2^2 x 3^1 x 5^1. Using the factor counting formula, we have the add one to each exponent and multiply them together to find the number of factors. factors making the answer.
Tom has twelve slips of paper which he wants to put into five cups labeled , , , , . He wants the sum of the numbers on the slips in each cup to be an integer. Furthermore, he wants the five integers to be consecutive and increasing from to . The numbers on the papers are and . If a slip with goes into cup and a slip with goes into cup , then the slip with must go into what cup?
- A.
- B.
- C.
- D.
- E.
The numbers have a sum of , which averages to , which means and will have the values and , respectively. Now, it's the process of elimination: Cup will have a sum of , so putting a slip in the cup will leave ; however, all of our slips are bigger than , so this is impossible. Cup has a sum of , but we are told that it already has a slip, leaving , which is too small for the slip. Cup is a little bit trickier but still manageable. It must have a value of , so adding the slip leaves room for . This looks good at first as we have slips smaller than that, but upon closer inspection, we see that no slip fits exactly. And the smallest sum of two slips is , which is too big, so this case is also impossible. Cup has a sum of , but we are told it already has a slip. So, we are left with , which is identical to Cup C and thus also impossible. With all other choices removed, we are left with the answer: Cup .
A baseball league consists of two four-team divisions. Each team plays every other team in its division games. Each team plays every team in the other division games with and . Each team plays a game schedule. How many games does a team play within its own division?
- A.
- B.
- C.
- D.
- E.
Solution 1
On one team they play games in their division and games in the other. This gives .
Since we start by trying M=5. This doesn't work because is not divisible by .
Next, does not work because is not divisible by .
We try does work by giving , and thus games in their division.
seems to work, until we realize this gives , but so this will not work.
Solution 2
, giving . Since , we have . Since is , we must have equal to , so .
This gives , as desired. The answer is .
One-inch squares are cut from the corners of this 5 inch square. What is the area in square inches of the largest square that can be fitted into the remaining space?

- A.
- B.
- C.
- D.
- E.
We draw a square as shown:
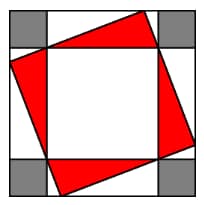
We want to find the area of the biggest square. The area of this square is composed of the center white square and the four red triangles. Because the inner square has an area of , , squared, , it also has a length of . The heights of each of the red triangles are 1 (because the gray squares have lengths of one), and the area of one triangle is namely . Thus, the combined area of the four triangles is . Furthermore, the area of the smaller square is . We add these to see that the area of the large square is .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
