2014 AMC 8
Complete problem set with solutions and individual problem pages
Harry and Terry are each told to calculate . Harry gets the correct answer. Terry ignores the parentheses and calculates . If Harry's answer is and Terry's answer is , what is ?
- A.
- B.
- C.
- D.
- E.
We have and . Clearly , so our answer is .
Paul owes Paula cents and has a pocket full of -cent coins, -cent coins, and -cent coins that he can use to pay her. What is the difference between the largest and the smallest number of coins he can use to pay her?
- A.
- B.
- C.
- D.
- E.
The fewest amount of coins that can be used is (a quarter and a dime). The greatest amount is , if he only uses nickels. Therefore we have .
Isabella had a week to read a book for a school assignment. She read an average of pages per day for the first three days and an average of pages per day for the next three days. She then finished the book by reading pages on the last day. How many pages were in the book?
- A.
- B.
- C.
- D.
- E.
Isabella read pages in the first 6 days. Although this can be calculated directly, it is simpler to calculate it as , which gives that she read pages. On her last day, she read more pages for a total of pages.
The sum of two prime numbers is . What is the product of these two prime numbers?
- A.
- B.
- C.
- D.
- E.
Since the two prime numbers sum to an odd number, one of them must be even. The only even prime number is . The other prime number is , and the product of these two numbers is .
Margie's car can go miles on a gallon of gas, and gas currently costs per gallon. How many miles can Margie drive on worth of gas?
- A.
- B.
- C.
- D.
- E.
Margie can afford gallons of gas. She can go miles on this amount of gas.
Six rectangles each with a common base width of have lengths of , and . What is the sum of the areas of the six rectangles?
- A.
- B.
- C.
- D.
- E.
Solution 1
The sum of the areas is equal to . This is equal to , which is equal to . This is equal to our final answer of .
Solution 2
we can just multiply the common width 2 by each of the lengths 1 by 1, the sum would be 182. This is slow and grouping the lengths is easier to. The answer is still .
There are four more girls than boys in Ms. Raub's class of students. What is the ratio of number of girls to the number of boys in her class?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let being the number of girls in the class. The number of boys in the class is equal to . Since the total number of students is equal to , we get . Solving this equation, we get . There are boys in our class, and our answer is .
Solution 2
To make the amount of boys and girls equal, 28 - 4 = 24. 24/2 = 12. The girls would need to be 12 + the 4 that we subtracted = 16. The boys would be 12. The ratio of girls to boys would be 16 : 12, but simplified would be 4 : 3. Thus, the answer is 4 : 3.
Eleven members of the Middle School Math Club each paid the same amount for a guest speaker to talk about problem solving at their math club meeting. They paid their guest speaker . What is the missing digit of this -digit number?
- A.
- B.
- C.
- D.
- E.
Solution 1
Since all the eleven members paid the same amount, that means that the total must be divisible by . We can do some trial-and-error to get , so our answer is
Solution 2
We know that a number is divisible by if the odd digits added together minus the even digits added together (or vice versa) is a multiple of . Thus, we have = a multiple of . The only multiple that works here is , as . Thus,
In , is a point on side such that and measures . What is the degree measure of ?
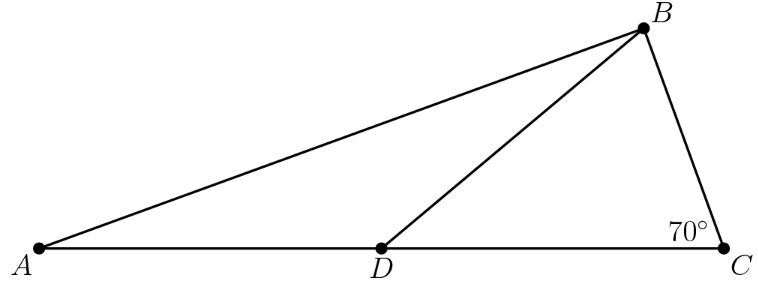
- A.
- B.
- C.
- D.
- E.
Using angle chasing is a good way to solve this problem. , so , because it is an isosceles triangle. Then . Since and are supplementary, .
The first AMC was given in and it has been given annually since that time. Samantha turned years old the year that she took the seventh AMC . In what year was Samantha born?
- A.
- B.
- C.
- D.
- E.
Since she was when she took the seventh AMC 8, she should be years old when the first AMC 8 occurred. Therefore, she was born or was 'age 0' in
Jack wants to bike from his house to Jill's house, which is located three blocks east and two blocks north of Jack's house. After biking each block, Jack can continue either east or north, but he needs to avoid a dangerous intersection one block east and one block north of his house. In how many ways can he reach Jill's house by biking a total of five blocks?
- A.
- B.
- C.
- D.
- E.
We can apply complementary counting and count the paths that DO go through the blocked intersection, which is . There are a total of paths, so there are paths possible. is the correct answer.
A magazine printed photos of three celebrities along with three photos of the celebrities as babies. The baby pictures did not identify the celebrities. Readers were asked to match each celebrity with the correct baby pictures. What is the probability that a reader guessing at random will match all three correctly?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let's call the celebrities A, B, and C. There is a chance that celebrity A's picture will be selected, and a chance that his baby picture will be selected. That means there are two celebrities left. There is now a chance that celebrity B's picture will be selected, and another chance that his baby picture will be selected. This leaves a chance for the last celebrity, so the total probability is . However, the order of the celebrities doesn't matter, so the final probability will be
Solution 2
There is a chance that the reader will choose the correct baby picture for the first person. Next, the second person gives a chance, and the last person leaves only 1 choice. Thus, the probability is
If and are integers and is even, which of the following is impossible?
- A.
and are even
- B.
and are odd
- C.
is even
- D.
is odd
- E.
none of these are impossible
Since is even, either both and are even, or they are both odd. Therefore, and are either both even or both odd, since the square of an even number is even and the square of an odd number is odd. As a result, must be even. The answer, then, is is odd.
Rectangle and right triangle have the same area. They are joined to form a trapezoid, as shown. What is ?
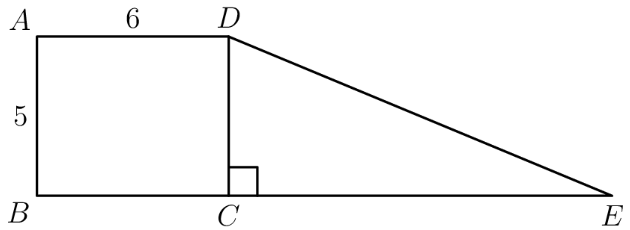
- A.
- B.
- C.
- D.
- E.
Solution 1
The area of is . The area of is , which also must be equal to the area of , which, since , must in turn equal . Through transitivity, then, , and . Then, using the Pythagorean Theorem, you should be able to figure out that is a triangle, so , or .
Solution 2
The area of the rectangle is Since the parallel line pairs are identical, . Let be . is the area of the right triangle. Solving for , we get According to the Pythagorean Theorem, we have a triangle. So, the hypotenuse has to be .
The circumference of the circle with center is divided into equal arcs, marked the letters through as seen below. What is the number of degrees in the sum of the angles and ?
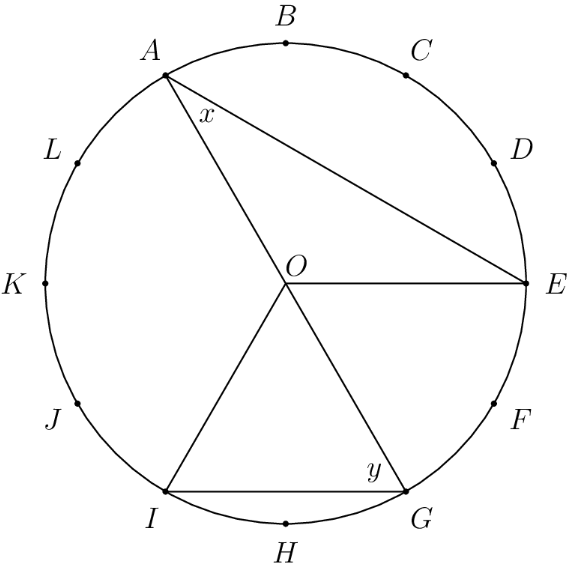
- A.
- B.
- C.
- D.
- E.
Solution 1
The measure of an inscribed angle is half the measure of its corresponding central angle. Since each unit arc is of the circle's circumference, each unit central angle measures . From this, , so . Also, , so . The number of degrees in the sum of both angles is
Solution 2
Since is isosceles and , . Since is isosceles and , . The number of degrees in the sum of both angles is .
The "Middle School Eight" basketball conference has teams. Every season, each team plays every other conference team twice (home and away), and each team also plays games against non-conference opponents. What is the total number of games in a season involving the "Middle School Eight" teams?
- A.
- B.
- C.
- D.
- E.
Within the conference, there are 8 teams, so there are pairings of teams, and each pair must play two games, for a total of games within the conference.
Each team also plays 4 games outside the conference, and there are 8 teams, so there are a total of games outside the conference.
Therefore, the total number of games is .
George walks mile to school. He leaves home at the same time each day, walks at a steady speed of miles per hour, and arrives just as school begins. Today he was distracted by the pleasant weather and walked the first mile at a speed of only miles per hour. At how many miles per hour must George run the last mile in order to arrive just as school begins today?
- A.
- B.
- C.
- D.
- E.
Note that on a normal day, it takes him hour to get to school. However, today it took hour to walk the first mile. That means that he has hours left to get to school, and mile left to go. Therefore, his speed must be , so is the answer.
Four children were born at City Hospital yesterday. Assume each child is equally likely to be a boy or a girl. Which of the following outcomes is most likely?
- A.
All are boys
- B.
All are girls
- C.
2 are boys and 2 are girls
- D.
3 are the same gender and 1 is not
- E.
They all have the same probability of happening
We'll just start by breaking cases down. The probability of A occurring is . The probability of B occurring is .
The probability of C occurring is , because we need to choose 2 of the 4 slots to be girls.
For D, there are two possible cases, 3 girls and 1 boy or 3 boys and 1 girl. The probability of the first case is because we need to choose 1 of the 4 slots to be a boy. However, the second case has the same probability because we are choosing 1 of the 4 children to be a girl, so the total probability is .
So out of the four fractions, D is the largest. So our answer is
A cube with -inch edges is to be constructed from smaller cubes with -inch edges. Twenty-one of the cubes are colored red and are colored white. If the -inch cube is constructed to have the smallest possible white surface area showing, what fraction of the surface area is white?
- A.
- B.
- C.
- D.
- E.
For the least possible surface area that is white, we should have 1 cube in the center, and the other 5 with only 1 face exposed. This gives 5 square inches of white, surface area. Since the cube has a surface area of 54 square inches, our answer is .
Rectangle has sides and . A circle of radius is centered at , a circle of radius is centered at , and a circle of radius is centered at . Which of the following is closest to the area of the region inside the rectangle but outside all three circles?
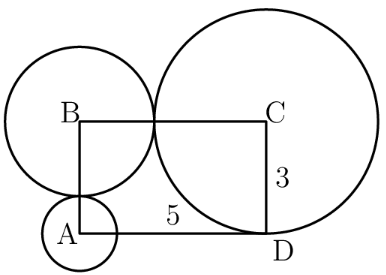
- A.
- B.
- C.
- D.
- E.
The area in the rectangle but outside the circles is the area of the rectangle minus the area of all three of the quarter circles in the rectangle.
The area of the rectangle is . The area of all 3 quarter circles is . Therefore the area in the rectangle but outside the circles is . is approximately and substituting that in will give
The -digit numbers and are each multiples of . Which of the following could be the value of ?
- A.
- B.
- C.
- D.
- E.
Solution 1
Since both numbers are divisible by 3, the sum of their digits has to be divisible by three. . To be a multiple of , has to be either or or and so on. We add up the numerical digits in the second number; . We then add two of the selected values, to , to get . We then see that C = or and so on, otherwise the number will not be divisible by three. We then add to , to get , which shows us that C = or or and so on. To be a multiple of three, we select a few of the common numbers we got from both these equations, which could be and . However, in the answer choices, there is no or or anything greater than , but there is a , so is our answer.
Solution 2
If is divisible by , the sum of it's digits should also be divisible by . This means that or . For equation , or . Logically, you can see the correlation between our first and second equations so we can make the assumption,
A -digit number is such that the product of the digits plus the sum of the digits is equal to the number. What is the units digit of the number?
- A.
- B.
- C.
- D.
- E.
We can think of the number as , where a is the tens digit and b is the unit digit. Since the number is equal to the product of the digits () plus the sum of the digits (), we can say that . We can simplify this to , which factors to . Dividing by , we have that . Therefore, the units digit, , is
Three members of the Euclid Middle School girls' softball team had the following conversation.
Ashley: I just realized that our uniform numbers are all -digit primes.
Bethany : And the sum of your two uniform numbers is the date of my birthday earlier this month.
Caitlin: That's funny. The sum of your two uniform numbers is the date of my birthday later this month.
Ashley: And the sum of your two uniform numbers is today's date.
What number does Caitlin wear?
- A.
- B.
- C.
- D.
- E.
The maximum amount of days any given month can have is , and the smallest two-digit primes are and . There are a few different sums that can be deduced from the following numbers, which are and , all of which represent the three days. Therefore, since Bethany says that the other two people's uniform numbers are earlier, so that means Caitlin and Ashley's numbers must add up to . Similarly, Caitlin says that the other two people's uniform numbers are later, so the sum must add up to . This leaves as today's date. From this, Caitlin was referring to the uniform wearers and , telling us that her number is , giving our solution as .
One day the Beverage Barn sold cans of soda to customers, and every customer bought at least one can of soda. What is the maximum possible median number of cans of soda bought per customer on that day?
- A.
- B.
- C.
- D.
- E.
In order to maximize the median, we need to make the first half of the numbers as small as possible. Since there are people, the median will be the average of the and largest amount of cans per person. To minimize the first , they would each have one can. Subtracting these cans from the cans gives us cans left to divide among people. Taking gives us and a remainder of . Seeing this, the largest number of cans the th person could have is , which leaves to the rest of the people. The average of and is . Thus our answer is .
A straight one-mile stretch of highway, 40 feet wide, is closed. Robert rides his bike on a path composed of semicircles as shown. If he rides at 5 miles per hour, how many hours will it take to cover the one-mile stretch?
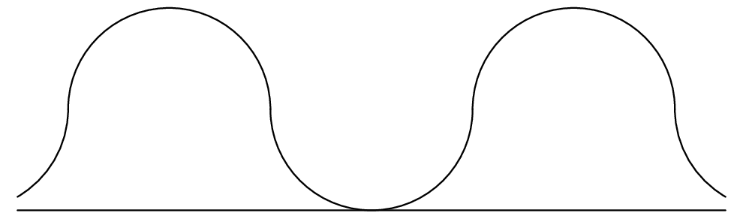
Note: 1 mile = 5280 feet
- A.
- B.
- C.
- D.
- E.
There are two possible interpretations of the problem: that the road as a whole is feet wide, or that each lane is feet wide. Both interpretations will arrive at the same result. However, let us stick with the first interpretation for simplicity. Each lane must then be feet wide, so Robert must be riding his bike in semicircles with radius feet and diameter feet. Since the road is feet long, over the whole mile, Robert rides semicircles in total. Were the semicircles full circles, their circumference would be feet; as it is, the circumference of each is half that, or feet. Therefore, over the stretch of highway, Robert rides a total of feet, equivalent to miles. Robert rides at miles per hour, so divide the miles by mph (because and time = distance/rate) to arrive at hours.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
