AMC 8 L2: Basic Geometry
Complete problem set with solutions and individual problem pages
As shown in the figure below, the correct expression to calculate the area of the trapezoid is .
- A.
- B.
- C.
- D.
N/A
Four friends, Art, Roger, Paul and Trisha, bake cookies, and all cookies have the same thickness. The shapes of the cookies differ, as shown.
Art’s cookies are trapezoids:
Roger’s cookies are rectangles:
Paul’s cookies are parallelograms:
Trisha’s cookies are triangles:
Each friend uses the same amount of dough, and Art makes exactly cookies.
(2003 AMC8 Problem, Question #8, #9, #10)
Rectangle and right triangle have the same area. They are joined to form a trapezoid, as shown. What is ? (2014 AMC8 Problem, Question #14)
- A.
- B.
- C.
- D.
- E.
Three identical rectangles are put together to form rectangle , as shown in the figure below. Given that the length of the shorter side of each of the smaller rectangles is feet, what is the area in square feet of rectangle ? (2019 AMC8 Problem, Question #2)
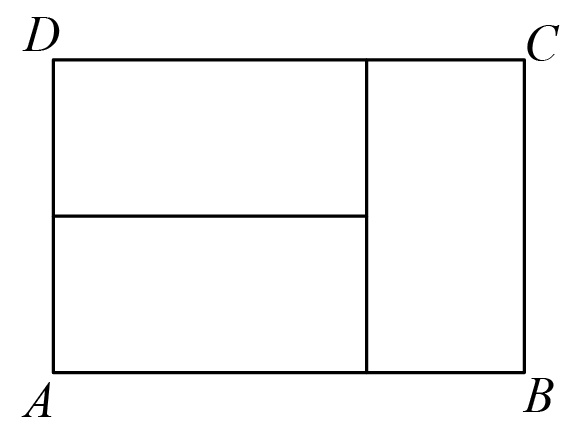
- A.
- B.
- C.
- D.
- E.
Points , , and are midpoints of the sides of the larger square. If the larger square has area , what is the area of the smaller square? (2006 AMC8 Problem, Question #05)
- A.
- B.
- C.
- D.
- E.
Solution : Drawing segements and , the number of triangles outside square is the same as the number of triangles inside the square. Thus areas must be equal so the area of is half the area of the larger square which is .
Solution : If the side length of the larger square is , the area of the smaller square is .
Thus, the area of the smaller square in the picture is .
Figure is a square. Inside this square three smaller squares are drawn with the side lengths as labeled. The area of the shaded L-shaped region is . (2000 AMC8 Problem, Question #6)
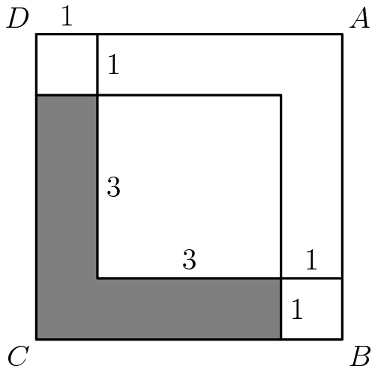
- A.
- B.
- C.
- D.
- E.
Solution :
Solution :
Which of the following polygons has the largest area? (2002 AMC8 Problem, Question #15)

- A.
- B.
- C.
- D.
- E.
Each polygon can be partitioned into unit squares and right triangles with sidelength . Count the number of boxes enclosed by each polygon, with the unit square being , and the triangle being being .. A has , B has , C has , D has , and E has . Therefore, the polygon with the largest area is .
The twelve-sided figure shown has been drawn on graph paper. What is the area of the figure in ? (2018 AMC8 Problem, Question #4)
- A.
- B.
- C.
- D.
- E.
We count unit squares in the middle, and small triangles each with an area of . Thus the answer is .
What is the area enclosed by the geoboard quadrilateral below? (2004 AMC8 Problem, Question #14)
- A.
- B.
- C.
- D.
- E.
Solution :

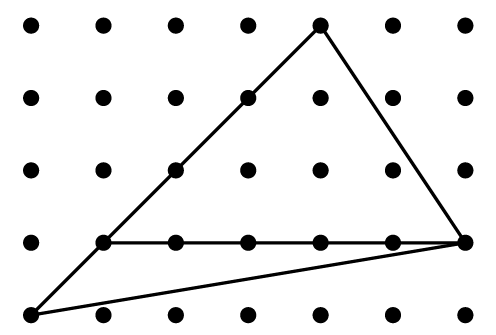
What is the area enclosed by the triangle below?
- A.
- B.
- C.
- D.
- E.
Solution :
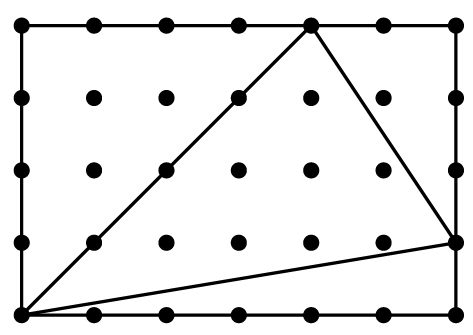
Solution :
In the diagram, all angles are right angles and the lengths of the sides are given in centimeters. Note the diagram is not drawn to scale. What is , in centimeters? (2012 AMC8 Problem, Question #5)
- A.
- B.
- C.
- D.
- E.
The figure is the same height on both sides, so the sum of the lengths contributing to the height on the left side will equal the sum of the lengths contributing to the height on the right side.
,
,
.
Thus, the answer is .
The letter is formed by placing two inch rectangles next to each other, as shown. What is the perimeter of the , in inches? (2006 AMC8 Problem, Question #6)

- A.
- B.
- C.
- D.
- E.
If the two rectangles were separate, the perimeter would be . It easy to see that their connection erases from each of the rectangles, so the final perimeter is .
The area of the shaded region in parallelogram is .
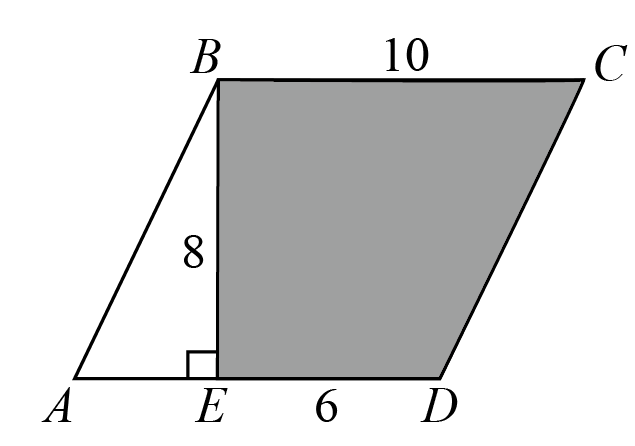
- A.
- B.
- C.
- D.
- E.
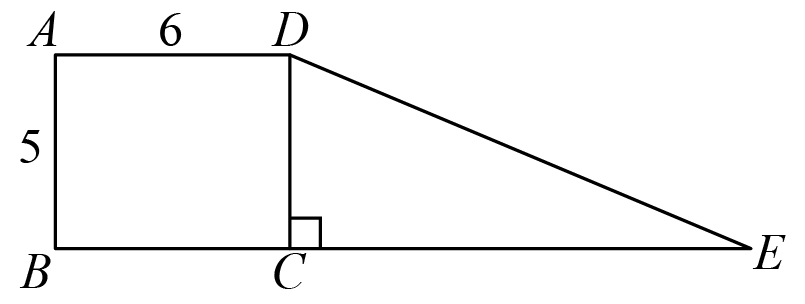
In trapezoid , is perpendicular to , , and . In addition, is on , and is parallel to . Find the area of . (2007 AMC8 Problem, Question #8)
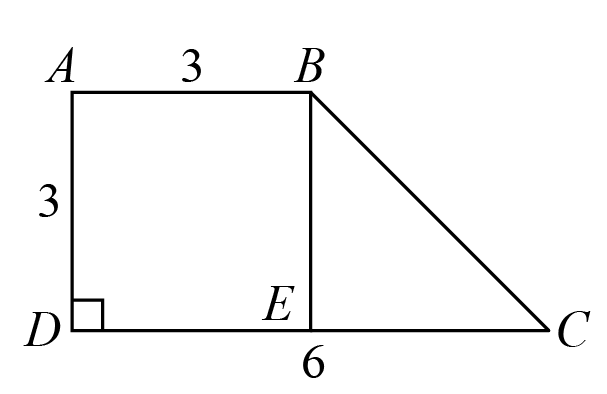
- A.
- B.
- C.
- D.
- E.
The cat shown has been drawn on graph paper. What is the area of the figure in cm?
- A.
- B.
- C.
- D.
N/A
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
