AMC 8 Daily Practice Round 11
Complete problem set with solutions and individual problem pages
.
- A.
- B.
- C.
- D.
- E.
Dividing both the numerator and the denominator by , we get:
Thus, the correct answer is .
As shown in the figure, the area of the unshaded region is square meters larger than the area of the shaded region. What is the area of the shaded region (in square meters)?
- A.
- B.
- C.
- D.
- E.
The ratio of the areas of the unshaded region to the shaded region is . Since the difference in their areas is square meters, the area of the shaded region is calculated as:
A shipping company charges the following rates: for a package weighing up to kilograms, the cost is dollars. For every kilogram exceeding kilograms, an additional dollars is charged per kilogram. If Emma ships a package weighing kilograms, how much in dollars does she need to pay?
- A.
- B.
- C.
- D.
- E.
.
Dan bought books for the classroom library. The most expensive book costs , and the least expensive book costs . Based on this, which of the following cannot be the total cost of the books?
- A.
- B.
- C.
- D.
- E.
The minimum total cost is calculated by taking 3 of the least expensive items and 1 of the most expensive item:
The maximum total cost is calculated by taking 3 of the most expensive items and 1 of the least expensive item
Thus, the total cost must be between and . Since the option is outside this range, it cannot be the total cost.
The length and width are both positive integers, and the area is . How many distinct rectangular shapes are possible?
- A.
- B.
- C.
- D.
- E.
, there are possibilities.
As shown in the figure, a cube's edges are painted either red or blue, ensuring that each face has at least one red edge. What is the minimum number of red edges required?
- A.
- B.
- C.
- D.
- E.
Select one red-painted edge for length, width, and height, ensuring that the chosen red edges are not in the same plane.
For example, as shown in the figure:
Thus, the correct answer is .
To increase the concentration of a -kilogram salt solution from to , how much water needs to be evaporated?
- A.
kg
- B.
kg
- C.
kg
- D.
kg
- E.
kg
The amount of salt in the solution remains unchanged before and after evaporation. Let kilograms of water be evaporated. Then, the equation is:
Solving for , we get:
Thus, the amount of water that needs to be evaporated is .
Three cards with the numbers , , and are available. If these three cards are randomly arranged to form a three-digit number, what is the probability that the resulting number is a multiple of ?
- A.
- B.
- C.
- D.
- E.
To solve the problem, we first list all possible three-digit numbers that can be formed using the digits , , and : . There are such numbers in total. A number is a multiple of if its last digit is . From the list, and meet this condition, so there are favorable outcomes. Using the probability formula, the probability of forming a number that is a multiple of is:
A new operation is defined as:
Given the equation:
What is the value that should be placed in ?
- A.
- B.
- C.
- D.
- E.
Observing the new operation, it calculates the average of two numbers.
First, treating the parentheses as a whole, the average of the number inside the parentheses and equals , meaning:
Thus, the average of and equals , leading to:
Thus, the correct answer is .
As shown in the figure, each small square has a side length of . What is the area of the shaded triangle?
- A.
- B.
- C.
- D.
- E.
Positive integer satisfies the equation: . What is the smallest value of ?
- A.
- B.
- C.
- D.
- E.
, , which is a perfect number, then .
Students from a middle school are attending a meeting in the auditorium. If each bench seats students, there will be students left standing. However, if each bench seats more students than before, there will be benches left unused. How many students are attending the meeting?
- A.
- B.
- C.
- D.
- E.
If each bench seats more students (i.e., students per bench), and there are unused benches, this means there are empty seats in total. The total number of benches is therefore
The total number of students is then
As shown in the figure, the coordinates of points and are and , respectively. The triangle is translated along the positive -axis so that point moves to point , forming the triangle . If , what are the coordinates of point ?
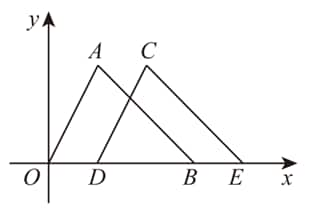
- A.
- B.
- C.
- D.
- E.
By analyzing the problem, we know that point satisfies . Since , we calculate . Therefore, is translated 1 unit to the right along the -axis to form . Point is also shifted 1 unit to the right, resulting in point having coordinates . Thus, the correct answer is .
A three-digit number is divided by , resulting in a quotient of and a remainder of , where both and are non-negative integers. What is the maximum possible value of ?
- A.
- B.
- C.
- D.
- E.
From the problem statement, the maximum possible value of is .
Since
and
the maximum value of is:
Thus, the correct answer is .
How many four-digit numbers satisfy the condition that the digit in the units place is greater than the digit in the thousands place, the digit in the thousands place is greater than the digit in the hundreds place, and the digit in the hundreds place is greater than the digit in the tens place?
- A.
- B.
- C.
- D.
- E.
Since the digits of the four-digit number must follow a strict order (units digit thousands digit hundreds digit tens digit), each selection of 4 distinct digits from to corresponds to exactly one valid number. This is because the order of the digits is uniquely determined by their sizes. Note that can be included in the selection, as it will occupy the smallest position (tens place) if chosen, satisfying the requirement that the leading digit (thousands place) cannot be . The total number of ways to choose 4 digits from to is:
Thus, there are such four-digit numbers.
As shown in the figure, the ancient Greeks often used small pebbles to form various shapes on the sand to study numbers. For example, the numbers are known as pentagonal numbers. What is the -th pentagonal number?

- A.
- B.
- C.
- D.
- E.
The sequence of pentagonal numbers is formed as follows:
Continuing the pattern, we calculate:
Thus, the 7th pentagonal number is .
There is a three-digit number , the sum of and is , and . What is the value of ?
- A.
- B.
- C.
- D.
- E.
None of the above
We can solve this problem using place value .
Step : Considering the Units Digit
If no borrowing occurs, we get:
Solving these equations:
.
However, if the minuend’s hundreds digit is , the difference cannot be , so borrowing must have occurred.
Step : Considering Borrowing
With borrowing, we modify the equation:
Rearranging:
Since , solving for and :
Step : Finding
By analyzing the tens and hundreds digits, we determine:
Thus, the three-digit number is .
Final Answer:
Thus, the correct answer is , which is .
Vivi forgot the password to her safe, but she remembers that it consists of four nonzero digits, and the sum of the digits is . What is the minimum number of attempts needed to guarantee opening the safe?
- A.
- B.
- C.
- D.
- E.
To find all possible passwords, we need to determine combinations of four nonzero digits that sum to . The valid combinations are ; ; ; ; ; and , resulting in six groups. For the combination , the digit can occupy any of the 4 positions, giving possibilities. For , can occupy 4 positions, can occupy 3 remaining positions, and fills the rest, yielding possibilities. Similarly, each of , , and also has possibilities. For , can occupy any of the 4 positions, giving possibilities. By the addition principle, the total number of passwords is:
Thus, Vivi needs to try at least attempts to guarantee opening the safe.
As shown in the figure, a grid is formed by squares of side length , and grid points (the intersections of the grid lines) are selected. A circle is drawn with center and radius . If exactly of the selected points (excluding ) lie inside the circle, what is the range of ?
- A.
- B.
- C.
- D.
- E.
Connect ,
Then, ,
,
,
,
,
,
,
,
Since .
When , there are exactly points lie inside the circle.
As shown in the figure, a circular piece of paper is cut into two sectors, and . The area of is , and the central angle of is larger than that of . What is the area of ?
- A.
- B.
- C.
- D.
- E.
Since the two sectors have the same radius, the ratio of their areas is equal to the ratio of their central angles. Given that the difference in their central angles is and the sum of their central angles is . We can solve for and . Hence, the ratio of their central angles is . It follows that the area ratio is also . Thus, the area of is .
What is the number of digits in the product ?
- A.
- B.
- C.
- D.
- E.
The product can be simplified as follows
Since , we have
Thus, the expression becomes
This represents a number with digits (the digits contribute 2 digits, and adds 32 zeros). Therefore, the product is a 34-digit number.
In a school club, of the members participate in community service, and of the members are involved in academic competitions. A total of members participate in both activities. How many members are involved only in academic competitions?
- A.
- B.
- C.
- D.
- E.
Let the total number of club members be represented as unit. Using the inclusion-exclusion principle, the total number of members can be calculated as:
Simplify the expression:
The number of members involved only in academic competitions is:
Thus, the number of members involved only in academic competitions is .
There are students, and no two students own the same set of books. However, each pair of students shares exactly one common book, and each book is owned by exactly two students. How many different books are there in total?
- A.
- B.
- C.
- D.
- E.
Represent the students as points , and use a line connecting two points to indicate that the corresponding pair of students shares exactly one common book. Since each book is owned by exactly two students, there is exactly one line between any two points.
To find the total number of books, we count the total number of lines in a complete graph with points. The number of lines (or edges) in a complete graph with points is given by:
For , the total number of lines is:
Thus, the students share a total of different books. The answer is .
A plane can fly for a maximum of hours in the air. On its journey, the plane travels at an average speed of going to its destination and on the return trip. What is the greatest distance (in kilometers) the plane can travel one way before it must turn back to ensure it does not exceed its flight time?
- A.
- B.
- C.
- D.
- E.
Let the maximum one-way distance the plane can travel be kilometers. Based on the problem, the equation is
Simplifying, we find
After verification, satisfies the original equation. Therefore, the plane can travel a maximum of one way.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
