AMC 8 Daily Practice Round 9
Complete problem set with solutions and individual problem pages
A bakery owner received a picnic order requiring sandwiches. If he can make one sandwich in seconds, how many minutes will it take him to complete the order?
- A.
- B.
- C.
- D.
- E.
The answer is .
Andy is drawing on a grid. He has drawn a small boat on a one-inch grid. What is the area of the boat in square inches?
- A.
- B.
- C.
- D.
- E.
Square:
Small trapezoid:
Big trapezoid:
In total:
The answer is .
A train took hours to travel kilometers from Applewood to Aurora, arriving hours late. What speed should it have traveled at to arrive on time?
- A.
- B.
- C.
- D.
- E.
The required time is now hours, while the distance remains kilometers.
∴ The required speed is .
The answer is .
Dino bought a giant jelly and plans to share it with his friends. He is going to make three cuts. What is the maximum number of pieces he can get?

- A.
- B.
- C.
- D.
- E.
By making two vertical cuts from top to bottom, the jelly is divided into pieces. Then, by making a horizontal cut through the middle, the jelly can be further divided into pieces.
The answer is .
Bill is choosing his courses for next year. He has to choosc two different courses, one from Foundational courses and one from Elective courses.
Foundational courses | Elective courses |
| Game AI | Game AI |
| Database system | Biology |
| Algebra | Italian |
| Geometry | History |
How many different pairs of combinations are possible?
- A.
- B.
- C.
- D.
- E.
It is worth noting that Game AI courses are both in Foundational courses and in elective courses.
.
The answer is .
A trapezoid has a top base of length , a bottom base of length , and two legs of lengths and , respectively. What is the area of the trapezoid?
- A.
- B.
- C.
- D.
- E.
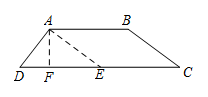
As shown in the diagram, draw through point , intersecting at point . Draw at point .
Since quadrilateral is a parallelogram, we have:
Also,
Given that , applying the Pythagorean theorem in right triangle , we find:
Thus, the area of trapezoid is:
Emily's teacher asks her to plot all the ordered pairs of positive integers, where represents the radius of a circle and represents the area of the same circle. What should her graph look like?
- A.
- B.
- C.
- D.
- E.
and present a quadratic function relationship.
The answer is .
Given that , and . Find the value of .
- A.
- B.
- C.
- D.
- E.
(∵)
.
The answer is .
The school's basketball team currently has boys and girls. The coach wants to randomly select people from the group to participate in the schools' basketball league. How many ways can the selected students be arranged such that at least one girl is included?
- A.
- B.
- C.
- D.
- E.
Number of choices of choosing students from students is:
Number of choices of choosing students from boys is:
.
The answer is .
What is the value of (Factorial can be used in the final result)?
- A.
- B.
- C.
- D.
- E.
;
The answer is .
A sequence of lights (either on or off) is used to represent numbers. The diagram provided shows the representations for the numbers to . Based on this pattern, what number does the sequence ●○○●●○ represent?
- A.
- B.
- C.
- D.
- E.
The given sequence can be converted into a binary number, where a lit light is represented as and an unlit light as .
Thus, the sequence ●○○●●○ corresponds to the binary number:
Converting this to decimal:
Thus, the number represented by the sequence is .
The answer is .
There are several boxes of cards, with each box containing the same number of cards.
- If only one box is distributed, and each child receives cards, there will be a shortage of cards.
- If all the boxes are distributed, each child receives cards, with cards remaining.
How many cards are there in each box?
- A.
- B.
- C.
- D.
- E.
Let there be children. Then, the number of cards in each box is , and the total number of cards is .
Since
it follows that must be either or .
Solving for , we get (since is discarded as it is not an integer).
Thus, the number of cards in each box is .
The answer is .
As shown in the figure, the cross-sections of cylindrical chopsticks are all circles with radius . What is the total length of the string needed to wrap around all chopsticks?
- A.
- B.
- C.
- D.
- E.
As shown in the figure, let and be the centers of the two circles, and let be their external common tangent with as the point of tangency.
Since , the same reasoning applies to each pair of adjacent circles, forming rectangles and circular sectors.
Since there are such tangents, their total length is:
The central angle corresponding to each arc is:
Thus, the arc length of each circular segment is:
The total string length consists of the straight segments and arc segments:
The answer is .
As shown in the figure, in triangle , the sides and are divided into five equal parts by four segments parallel to . If the area of is , what is the sum of the areas of the shaded regions labeled ② and ④?
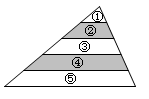
- A.
- B.
- C.
- D.
- E.
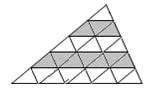
From the graph, .
The answer is .
A switch is connected to three independent light bulbs, meaning each bulb operates independently of the others. When the switch is pressed, each bulb has a probability of turning on. What is the probability that at least two bulbs will light up with a single press of the switch?
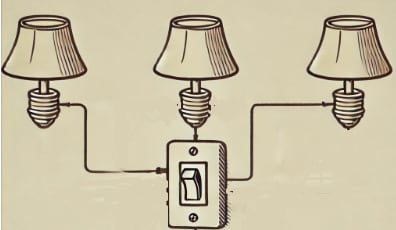
- A.
- B.
- C.
- D.
- E.
The probability of two bulbs being on and one bulb being off is:
The probability of all three bulbs being on is:
Thus, the total probability is:
Among the natural numbers from to , how many numbers are not multiples of , not multiples of , and not multiples of ?
- A.
- B.
- C.
- D.
- E.
Among the natural numbers from to :
- Multiples of :
- Multiples of :
- Multiples of :
- Multiples of both and :
- Multiples of both and :
- Multiples of both and :
- Multiples of , , and :
Using the principle of Inclusion-Exclusion, the total count of numbers that are multiples of 2, 3, or 5 is:
Thus, the count of numbers not being multiples of , , or is:
The answer is .
An opaque bag contains two balls, one red and one black, which are identical in size and shape. A ball is randomly drawn from the bag three times, with replacement. If drawing a red ball earns points and drawing a black ball earns point, what is the probability that the total score after three draws is exactly points?
- A.
- B.
- C.
- D.
- E.
The possible total scores after draws are , , , and , resulting in different cases.
- The probability of scoring points (drawing three black balls) is:
- The probability of scoring points (drawing three red balls) is:
- Scoring points requires red ball and black balls.
- Scoring points requires red balls and black ball.
Since there are only two types of balls, each ball has an equal probability of being drawn ( per draw). The probabilities of scoring and must be the same.
Thus, the probability of scoring points is:
The answer is .
A total of unit cubes, each with an edge length of , are stacked together to form a solid shape. What is the minimum possible surface area of the resulting geometric figure?
- A.
- B.
- C.
- D.
- E.

The surface area is minimized when the unit cubes overlap as much as possible.
Consider a cube composed of unit cubes (), which has the smallest possible surface area when fully assembled.
To reduce the total count to unit cubes, we need to remove cubes in a way that does not increase the surface area. This can be achieved by removing:
. Two cubes from two different corners, or
. Two adjacent cubes from the same corner.
In both cases, the surface area remains unchanged at .
Thus, the minimum possible surface area of the resulting shape is .
The answer is .
A pile of fruit has its water content decrease from to after being stored for a long period. By what percentage has the total weight of the fruit decreased?
- A.
- B.
- C.
- D.
- E.
Let the original total weight be . Then, the weight of the non-water part is .
Now, with the water content at , the weight of the non-water part is , so the non-water weight becomes:
Thus, the total weight decreased by:
The answer is .
Given that the of consecutive even numbers is times of the larger number. What is the square difference between these two integers?
- A.
- B.
- C.
- D.
- E.
Let be half of the larger integer.
,
∴ These two integers are and .
The answer is .
Alice has four grandchildren of different ages, all under , and the product of their ages is . What is the sum of their ages?
- A.
- B.
- C.
- D.
- E.
The ages of four children are , and .
So the sum of their ages is .
As shown in the diagram, if are distinct nonzero digits, and the two-digit numbers and , formed in the counterclockwise direction, are both multiples of , then what is the sum of the largest and smallest possible three-digit numbers that can be formed?
- A.
- B.
- C.
- D.
- E.
Since the two-digit numbers and are both multiples of , they must be one of the following:
From these, the valid three-digit numbers that can be formed are:
The largest three-digit number is , and the smallest is . Their sum is:
The answer is .
As shown in the figure, a rectangle with length and width rolls continuously along the positive -axis for times. The point sequentially lands at positions . What are the coordinates of ?
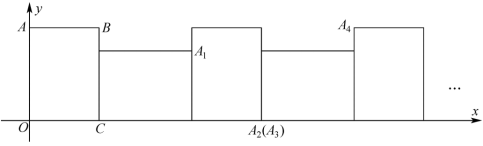
- A.
- B.
- C.
- D.
- E.
From the given conditions, we obtain the following sequence of coordinates for point :
Since every four rolls form a cycle, we analyze the displacement per cycle. Each full cycle results in a horizontal shift of:
Thus, after one full cycle, point moves units to the right.
The additional positions within a cycle are as follows:
- After one extra roll, moves units further, and the -coordinate is .
- After two extra rolls, moves units further, and the -coordinate is .
- After three extra rolls, the coordinates are the same as after two extra rolls.
Since:
Point completes full cycles and moves one extra step beyond that.
Thus, the final coordinates are:
The answer is .
Among five pairs of distinct shoes, four shoes are randomly selected. How many ways can at least one matching pair be formed?
- A.
- B.
- C.
- D.
- E.
The total number of ways to choose any shoes from shoes is:
The number of ways to select shoes without forming any complete pair is:
- Choose different pairs out of the available:
- For each selected pair, choose one shoe ( choices per pair):
- Total ways to pick shoes without forming a pair:
Thus, the number of ways to select shoes with at least one matching pair is:
The answer is .
How many four-digit numbers can be formed using the digits (digits may be repeated) such that they satisfy the condition:
- A.
- B.
- C.
- D.
- E.
We classify the four-digit numbers into four cases:
① All four digits are the same. Possible numbers:
Total: numbers.
② Two different digits appear twice each. For example, numbers like .
We choose two different digits from , which can be done in ways.
Each choice allows different digit arrangements, so this case contributes:
③ Three different digits appear, with one digit repeated. Examples include .
The valid digit sum conditions are and , giving valid digit sets.
Each set allows different digit arrangements, so this case contributes:
④ All four digits are different. Valid numbers include , totaling:
Adding all cases together:
The answer is .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
