AMC 8 Daily Practice Round 7

Complete problem set with solutions and individual problem pages

Problem 1 Easy

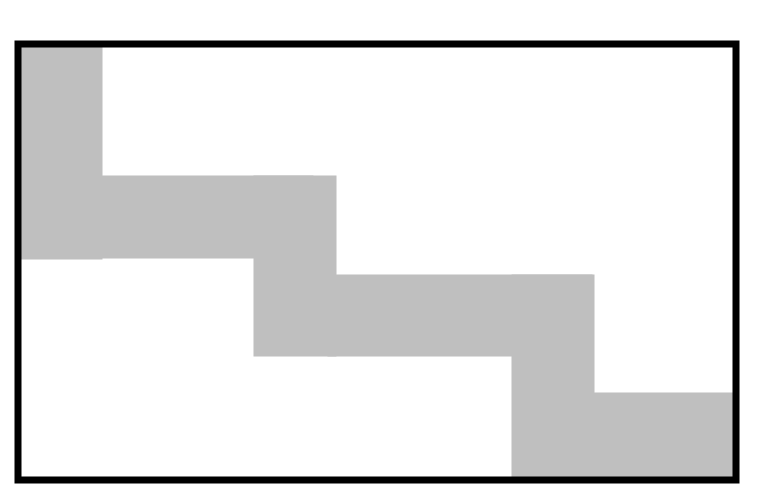
The following figure is a side view of a staircase. It is known that each step is 30 cm wide and 20 cm high. What is the perimeter of the side of this staircase in meters?

  • A.

    4

  • B.

    8

  • C.

    16

  • D.

    400

  • E.

    800

Answer:B

Through translation, it can be known that the length BC of the staircase in the figure is 30 \times 8 = 240 cm, and the height AB of the staircase is 20 \times 8 = 160 cm.

Therefore, the perimeter of the side of the staircase is 240 + 160 + (30 + 20) \times 8 = 800 \text{ cm}.

Note the unit conversion: 800 \text{ cm} = 8 \text{ m}.

Thus, the final answer is \boxed{8}m .

Link Problem
Problem 2 Easy

A large rectangle is divided into four pieces. Given that the perimeter of piece A is 8 cm, the perimeter of piece B is 30 cm, and the perimeter of piece D is 38 cm, what is the perimeter of the large rectangle?

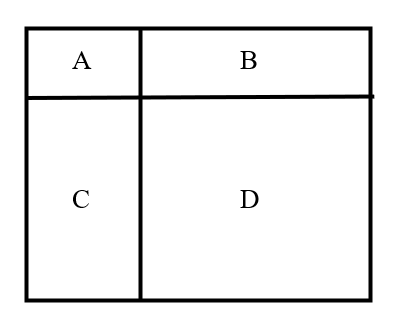
  • A.

    42cm

  • B.

    44cm

  • C.

    46cm

  • D.

    48cm

  • E.

    50cm

Answer:C

Using the translation method, we know that:

The perimeter of the large rectangle = the perimeter of piece A + the perimeter of piece D, which is 8 + 38 = 46 cm.

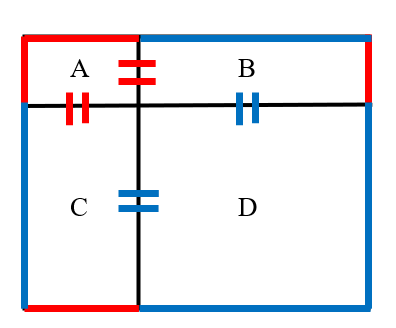
Final answer: \boxed{46cm}.

Link Problem
Problem 3 Easy

In the diagram, all angles are right angles and the lengths of the sides are given in centimeters.Note the diagram is not drawn to scale. What is the length in X, in centimeters?

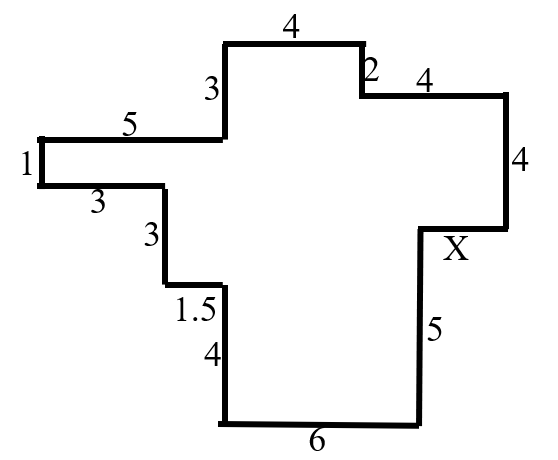
  • A.

    3

  • B.

    2.5

  • C.

    1.3

  • D.

    2

  • E.

    3.5

Answer:B

Using the translation method, we find that:

5 + 4 + 4 = 3 + 1.5 + 6 + X

Solving for X:

13 = 10.5 + X \Rightarrow X = 13 - 10.5 = 2.5

Thus, the length of X is 2.5cm.

Link Problem
Problem 4 Easy

In the backyard, there is a rectangular flower bed with a square vegetable garden inside it. Emily wants to put a fence around its outer edge. What is the perimeter of the flower bed in feet?

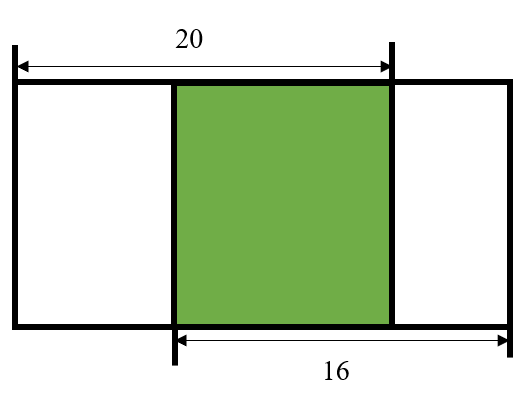
  • A.

    70

  • B.

    72

  • C.

    74

  • D.

    76

  • E.

    78

Answer:B

The perimeter of the rectangle = AD + DE+EH + HA=AB + BC + CD + DE+EF + FG + GH + HA.

Since AB + BC = 20, EF + FG=16, and BC = DE = FG = HA, AB = GH, CD = EF, we can calculate the perimeter of the rectangle as follows:

The perimeter of the rectangle

=AB + BC+GH + HA + EF+FG + CD + DE

=(AB + CD)\times2+(EF + FG)\times2

=2\times20 + 2\times16=40 + 32=72

So the perimeter of the rectangular flower bed is 72 feet.

Link Problem
Problem 5 Easy

A figure is formed by arranging 22 small pieces of paper of the same size as shown in the diagram. Given that the length of each small piece of paper is 15 centimeters, what is the total perimeter of the shaded parts in the figure?

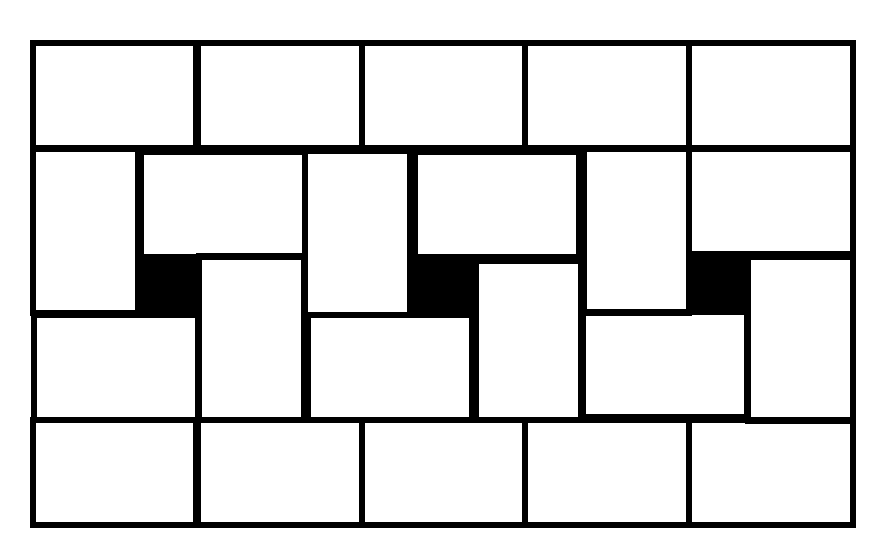
  • A.

    15cm

  • B.

    20cm

  • C.

    45cm

  • D.

    60cm

  • E.

    75cm

Answer:D

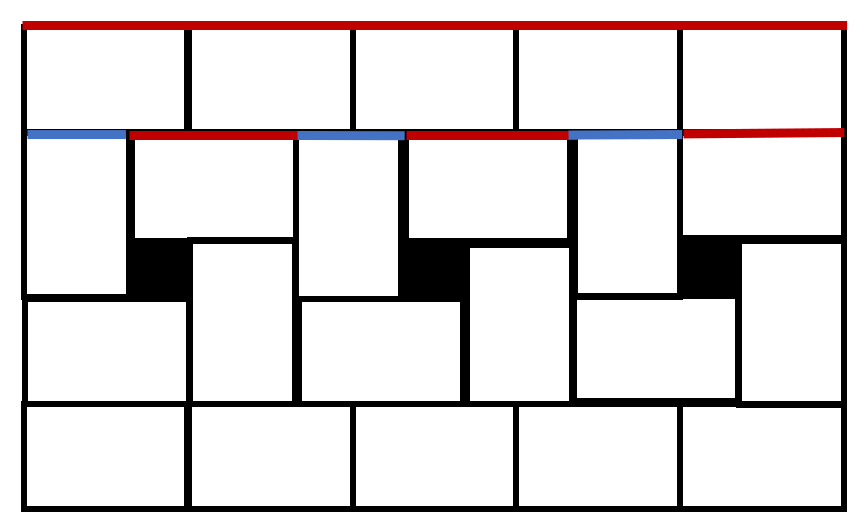
As shown in the diagram, we can observe that 5 lengths =3 lengths +3 widths.

Therefore, 2 lengths =3 widths.

Given that the length is 15\text{ cm}, the width can be calculated as follows: \text{Width} = 15 \times 2 \div 3 = 10cm.

The perimeter of one shaded part is \text{length} - \text{width} = 15 - 10 = 5 cm.

Thus, the total perimeter of the shaded parts is: 5 \times 4 \times 3 = 60cm.

Link Problem
Problem 6 Easy

There is a rectangular flower bed. In the middle of the flower bed, there is a pedestrian path with a width of 3 meters. The flower bed is 53 meters long and 25 meters wide. What is the area of the pedestrian path in square meters?

  • A.

    200

  • B.

    225

  • C.

    234

  • D.

    245

  • E.

    260

Answer:B

Through observation, we can translate the path to the position as shown in the following figure.

Therefore, the area of the pedestrian path is calculated as: 25 \times 3 + (53 - 3) \times 3 = 225

Link Problem
Problem 7 Easy

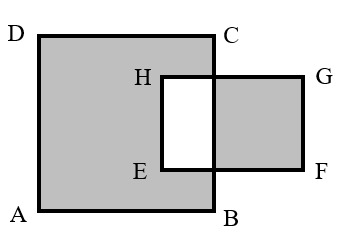
As shown in the figure below, the side length of square ABCD is 10 centimeters, and the rectangle EFGH has a length of 8 centimeters and a width of 5 centimeters. What is the difference between the areas of the two shaded parts?

  • A.

    15

  • B.

    20

  • C.

    30

  • D.

    40

  • E.

    60

Answer:E

 

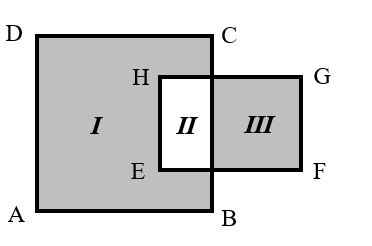
As shown in the figure, let the areas of the three regions be denoted as Ⅰ, Ⅱ, and Ⅲ respectively.

We have:

Ⅰ = \text{Area of square } ABCD - Ⅱ

Ⅲ = \text{Area of rectangle } EFGH - Ⅱ

Then, the difference between the areas of the two shaded parts is: Ⅰ - Ⅲ = \left( \text{Area of square } ABCD - Ⅱ \right) - \left( \text{Area of rectangle } EFGH - Ⅱ \right) = \text{Area of square } ABCD - \text{Area of rectangle } EFGH = 10 \times 10 - 8 \times 5 = 100 - 40 = 60

Link Problem
Problem 8 Easy

A large square and a small square are placed side by side, with the side length of the small square being 6cm. What is the area of the shaded part?

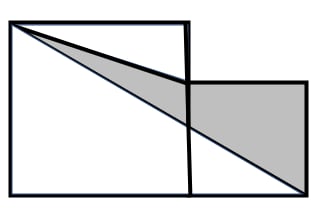
  • A.

    25 cm^{2}

  • B.

    28 cm^{2}

  • C.

    32 cm^{2}

  • D.

    36 cm^{2}

  • E.

    40 cm^{2}

Answer:D

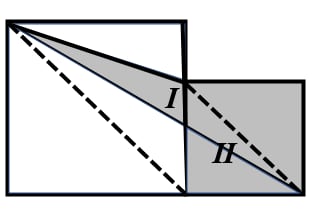
As shown in the figure, connect the diagonals of the two squares.

Since the two diagonals are parallel, we find that the area of triangle Ⅰ is equal to the area of triangle Ⅱ.

Therefore, the area of the shaded part is converted to the area of the small square, which is: 6 \times 6 = 36 cm^{2}

Link Problem
Problem 9 Easy

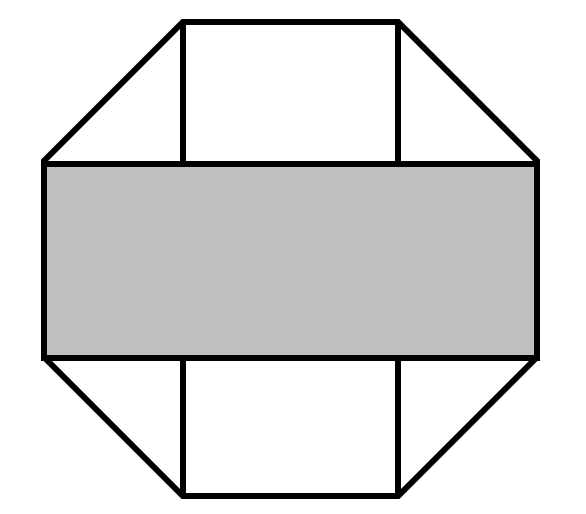
The area of a regular octagon is 40 square centimeters. What fraction of the area of the octagon is shaded?

  • A.

    \frac{1}{3}

  • B.

    \frac{15}{32}

  • C.

    \frac{1}{2}

  • D.

    \frac{3}{5}

  • E.

    \frac{9}{16}

Answer:C

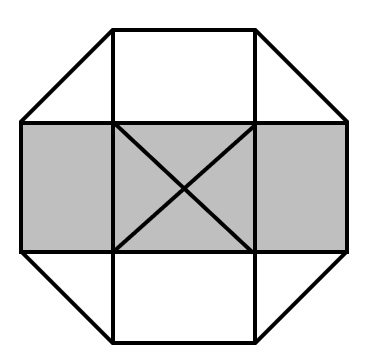
By means of division, the octagon is divided into 4 rectangles and 8 triangles.

The shaded part contains 2 rectangles and 4 triangles.

Therefore, the area of the shaded part accounts for \frac{1}{2} of the total area.

Link Problem
Problem 10 Medium

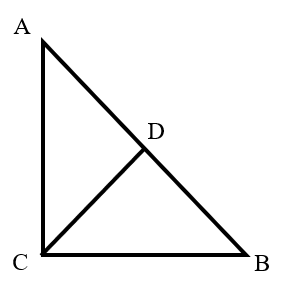
In parallelogram ABCD, E and F are the midpoints of AD and CD respectively. Given that EF = 4 and FB = 6, what is the area of the parallelogram?

  • A.

    20

  • B.

    25

  • C.

    32

  • D.

    40

  • E.

    64

Answer:C

Draw EG through point E parallel to CD, and draw FH through point F parallel to AD.

We observe that:

The area of \triangle ABE is \frac{1}{4} of the area of the parallelogram.

The area of \triangle BCF is \frac{1}{4} of the area of the parallelogram.

The area of \triangle DEF is \frac{1}{8} of the area of the parallelogram.

Therefore, the area of \triangle EFB is \frac{3}{8} of the area of the parallelogram.

The area of \triangle EFB is calculated as: \frac{4 \times 6}{2} = 12.

Let the area of the parallelogram be A.

Then: \frac{3}{8}A = 12.

Solving for A: A = 12 \div \frac{3}{8} = 32.

Thus, the area of the parallelogram is 32.

Link Problem
Problem 11 Easy

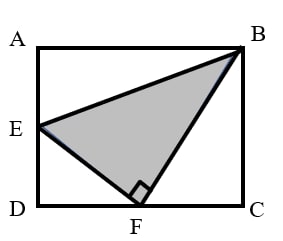
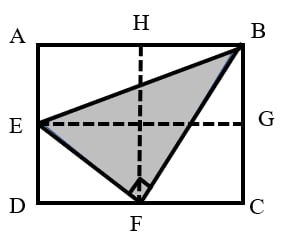
As shown in the figure, in triangle ABC, m\angle ACB = 90^\circ, BC = 1, point D is the midpoint of side AB, and CD bisects the perimeter of triangle ABC. What is the length of BD?

  • A.

    \frac{\sqrt{2}}{4}

  • B.

    \frac{\sqrt{2}}{2}

  • C.

    1

  • D.

    \sqrt{2}

  • E.

    2

Answer:B

Since CD bisects the perimeter of triangle ABC, the perimeter of triangle ACD is equal to the perimeter of triangle BCD.

That is: AC + AD + CD = BC + BD + CD.

Simplifying, we get: AC + AD = BC + BD.

Since D is the midpoint of AB, AD = BD.

Substituting this into the equation above, we have: AC = BC

Given BC = 1, it follows that AC = 1.

In the right triangle ABC with \angle ACB = 90^\circ, by the Pythagorean theorem: AB = \sqrt{AC^2 + BC^2} = \sqrt{1^2 + 1^2} = \sqrt{2}.

Since D is the midpoint of AB, the length of BD is: BD = \frac{AB}{2} = \frac{\sqrt{2}}{2}.

Link Problem
Problem 12 Easy

In a triangle, the largest angle is 5 times the smallest angle, and the other angle is 3 times the smallest angle. What is the degree measure of the largest angle?

  • A.

    90

  • B.

    92.5

  • C.

    100

  • D.

    102.5

  • E.

    112.5

Answer:C

Let the three angles of the triangle be m\angle A, m\angle B, and m\angle C, where m\angle A < m\angle B < m\angle C.

According to the problem, we know that m\angle C = 5m\angle A and m\angle B = 3\angle a.

Thus, the ratio of the angles is m\angle A : m\angle B : m\angle C = 1 : 3 : 5.

Since the sum of the interior angles of a triangle is 180^\circ, the measure of the largest angle \angle C is: m\angle C = 180^\circ \div (1 + 3 + 5) \times 5 = 100^\circ.

Link Problem
Problem 13 Easy

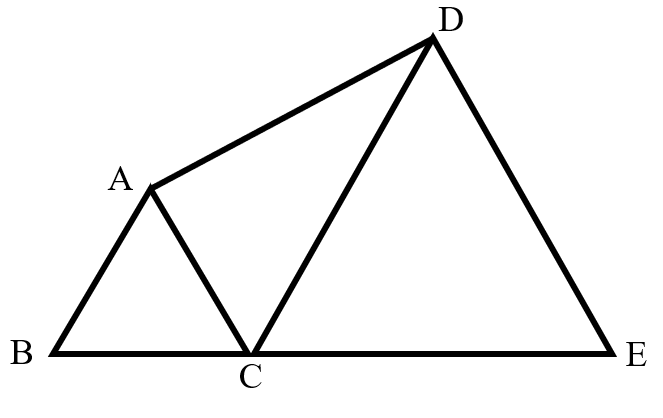
Two equilateral triangles ABC and DCE lie on the same horizontal plane, with areas 4 and 9 respectively. What is the area of triangle ACD?

  • A.

    5

  • B.

    6

  • C.

    6.5

  • D.

    7

  • E.

    8

Answer:B

Since triangles ABC and DCE are equilateral, AB \parallel DC and AC \parallel DE.

Given that the area of a triangle is \frac{1}{2} \times \text{base} \times \text{height}, we have:

\text{Area of } \triangle ABC : \text{Area of } \triangle ACD=AB : DC

\text{Area of } \triangle ACD : \text{Area of } \triangle CDE=BC : DE

Since AB = BC and DC = DE , it follows that: \text{Area of } \triangle ABC : \text{Area of } \triangle ACD = \text{Area of } \triangle ACD : \text{Area of } \triangle CDE.

Let the area of \triangle ACD be A.

Then: A^2 = \text{Area of } \triangle ABC \times \text{Area of } \triangle CDE = 4 \times 9.

Solving for A: A = \sqrt{4 \times 9} = 6.

Thus, the area of \triangle ACD is 6.

Link Problem
Problem 14 Easy

The perimeter of a triangle is 60cm, and its shortest side is 13cm. If all three sides of the triangle are integers, what is the maximum possible length of the longest side in centimeters?

  • A.

    24

  • B.

    25

  • C.

    28

  • D.

    29

  • E.

    30

Answer:D

Assume the three sides of the triangle, arranged in ascending order, are 13, a, and b.

According to the triangle inequality theorem, the sum of any two sides of a triangle must be greater than the third side, so: 13 + a > b.

Since the perimeter of the triangle is 60 cm, we have: 13 + a + b = 60, which simplifies to: a = 47 - b.

Substituting a = 47 - b into the inequality 13 + a > b, we get: 13 + (47 - b) > b, 60 - b > b, 60 > 2b, b < 30.

Since b is an integer, the maximum possible value of b is 29.

Thus, the longest side can be at most 29 centimeters.

Link Problem
Problem 15 Easy

What is the largest whole number smaller than the perimeter of any triangle with a side of length 4 and a side of length 91?

  • A.

    182

  • B.

    184

  • C.

    186

  • D.

    188

  • E.

    190

Answer:A

From the Triangle Inequality Theorem, we know that for the third side s of the triangle, the following must hold: s < 4 + 91 = 95 and s > 91 - 4 = 87.

Let P be the perimeter of the triangle, so P = 4 + 91 + s.

Adding 4 + 91 to all parts of the inequality for s, we get: 87 + 4 + 91 < P < 95 + 4 + 91

182 < P < 190

Thus, the largest whole number smaller than the perimeter of any such triangle is 182.

Link Problem
Problem 16 Easy

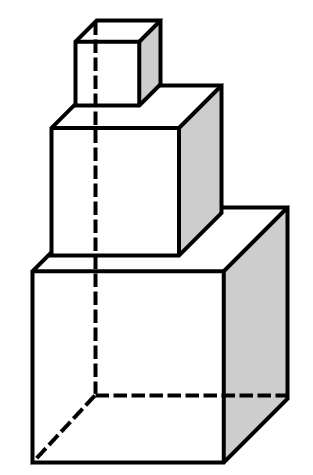
As shown in the figure below, three cubes with edge lengths of 1cm, 2cm, and 3cm are attached closely together. What is the surface area of the resulting three-dimensional figure in square centimeters?

  • A.

    74

  • B.

    77

  • C.

    80

  • D.

    83

  • E.

    84

Answer:A

Through observation, we find that when the three cubes are attached closely together, some surfaces are covered:

the bottom surface of cube A, part of the top and bottom surfaces of cube B, and part of the top surface of cube C.

The total surface area is calculated as follows: 6 \times 1^2 + 6 \times 2^2 + 6 \times 3^2 - 2 \times 1^2 - 2 \times 2^2 = 74 cm^{2}.

Link Problem
Problem 17 Easy

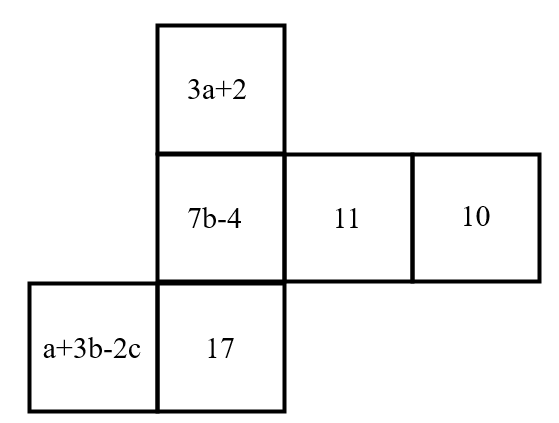
The following is a plane development diagram of a cube. If the values on the two opposite faces of the cube are equal, what is the value of a - b \times c?

  • A.

    3

  • B.

    4

  • C.

    5

  • D.

    8

  • E.

    10

Answer:C

Through observation, we find three pairs of opposite faces as shown in the figure.

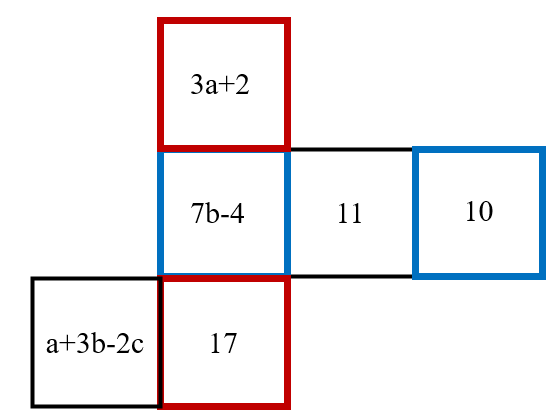
Since the values on opposite faces are equal, we have the following equations:

3a + 2 = 17

7b - 4 = 10

a + 3b - 2c = 11

Solving these equations: -

From 3a + 2 = 17, we get 3a = 15, so a = 5.

From 7b - 4 = 10, we get 7b = 14, so b = 2. -

Substituting a = 5 and b = 2 into a + 3b - 2c = 11, we have 5 + 3 \times 2 - 2c = 11, which simplifies to 11 - 2c = 11, so c = 0.

Finally, we calculate a - b \times c: a - b \times c = 5 - 2 \times 0 = 5

Link Problem
Problem 18 Easy

Mike folded a piece of paper into a cube-shaped box, put a gift inside, and mixed it with the boxes below. Which box contains the gift?

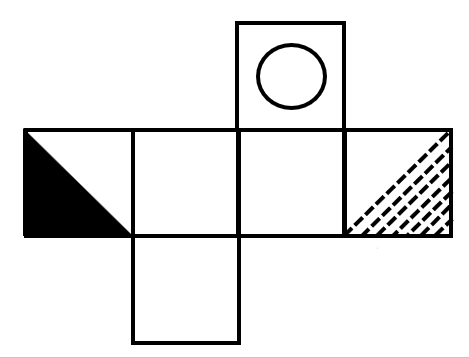
  • A.

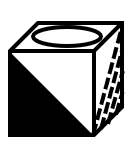
  • B.

  • C.

  • D.

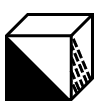
  • E.

Answer:B

As shown in the figure, first identify the corresponding faces in the cube.

Based on the characteristics and positions of various symbols in the unfolded diagram, it is found that the black triangle and the slanted-line triangle should be adjacent faces with one side overlapping.

Therefore, the correct choice is B.

Link Problem
Problem 19 Easy

There is a cylindrical part with a height of 10 centimeters and a base diameter of 6 centimeters. One end of the part has a straight cylindrical hole, as shown in the figure: the diameter of the circular hole is 4 centimeters, and the depth of the hole is 5 centimeters. If the parts of this component that are exposed to air are to be painted with anti-rust paint, what is the total area to be painted in square centimeters?(For convenience, use \pi = 3.14.)

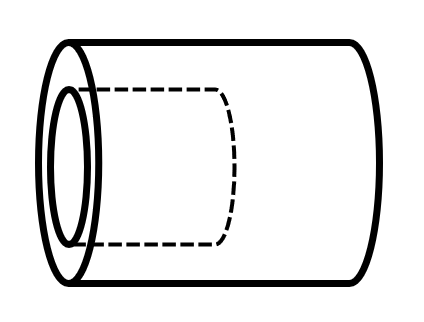
  • A.

    282.6

  • B.

    292.02

  • C.

    307.72

  • D.

    326.56

  • E.

    320.28

Answer:C

The total area to be painted includes the outer surface area of the cylinder, the inner surface area of the hole, and the area of the two circular bases (adjusted for the hole).

The calculation is as follows: 3.14 \times \left(\frac{6}{2}\right)^2 \times 2 + 3.14 \times 6 \times 10 + 3.14 \times 4 \times 5 = 307.72

The total area to be painted is 307.72 square centimeters.

Link Problem
Problem 20 Easy

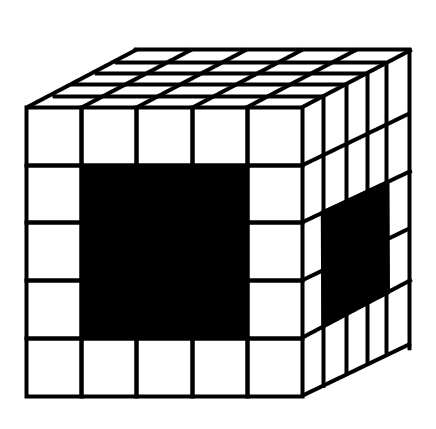
There is a cube wooden block with an edge length of 5cm. There are penetrating holes (shown as black parts in the figure) when viewed from the front and the right side. What is the volume of this three-dimensional figure in cubic centimeters?

  • A.

    54

  • B.

    56

  • C.

    62

  • D.

    68

  • E.

    74

Answer:D

We can calculate the volume by dividing the cube into five layers from top to bottom:

The first and fifth layers have no holes, and the volume of each layer is 5 \times 5 \times 1 = 25 cubic centimeters.

The volume of the second layer is 10 \times 1 = 10 cubic centimeters.

The volume of the third layer is 4 \times 1 = 4 cubic centimeters.

The volume of the fourth layer is 4 \times 1 = 4 cubic centimeters.

Adding them up, the total volume is: 25 + 25 + 10 + 4 + 4 = 68 cubic centimeters.

Link Problem
Problem 21 Easy

A part of a circular glass mirror is damaged. To obtain a mirror of the same size, a worker uses a right-angle ruler for measurement as shown in the figure, and finds that AB = 12cm and BC = 5cm. What is the diameter of the circular mirror in centimeters?

  • A.

    10

  • B.

    11

  • C.

    12

  • D.

    13

  • E.

    14

Answer:D

It is known that the circumferential angle subtended by a diameter is a right angle.

Therefore, connecting AC forms a right triangle ABC with \angle ABC = 90^\circ, and AC is the diameter of the circular mirror.

By the Pythagorean theorem in \triangle ABC: AC = \sqrt{AB^2 + BC^2} = \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13

Thus, the diameter of the circular mirror is 13 centimeters.

Link Problem
Problem 22 Easy

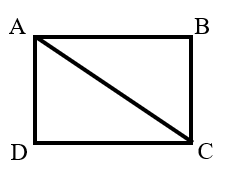
As shown in the figure, ABCD is a rectangle with length 4, width 3, and diagonal length 5. It is rotated 90^\circ clockwise around point C. Find the area swept by side AB.(Take \pi=3.14)

  • A.

    7.065

  • B.

    9.42

  • C.

    12.56

  • D.

    15.7

  • E.

    19.625

Answer:C

The area swept by side AB is the area of the shaded part in the figure.

The area swept by AB = (\text{Area of sector } ACA' + \text{Area of } \triangle A'B'C) -(\text{Area of sector } BCB' + \text{the area of } \triangle ABC).

Since the area of \triangle ABC is equal to the area of \triangle A'B'C, this simplifies to: \text{Area of sector } ACA' - \text{Area of sector } BCB'.

Calculating the areas of the sectors :

= \pi \times 5^2 \times \frac{1}{4} - \pi \times 3^2 \times \frac{1}{4}

= \pi \times 25 \times \frac{1}{4} - \pi \times 9 \times \frac{1}{4}

= \pi \times (25 - 9) \times \frac{1}{4} = \pi \times 16 \times \frac{1}{4}

= 4\pi = 12.56 \quad (\text{taking } \pi \approx 3.14)

Answer: The areas swept by sides AB is 12.56 square units.

Link Problem
Problem 23 Easy

In the figure on the right, two sectors with central angles of 90^\circ are placed on top of a large circle, and a small circle is placed on top of the two sectors. All four shapes share the same center. If the ratio of the radii of the small circle, the large circle, and the sectors is 1 : 3 : 4, what percentage of the total area is occupied by the shaded region?

  • A.

    32\%

  • B.

    20\%

  • C.

    28\%

  • D.

    36\%

  • E.

    40\%

Answer:A

Let the radii of the large circle, the small circle, and the sectors be r, 3r, and 4r respectively.

 

The total area of the logo is

\frac{1}{2}\pi (4r)^2 + \frac{1}{2}\pi (3r)^2 = 12.5\pi r^2.

 

The area of the shaded region is

\frac{1}{2}\pi (3r)^2 - \frac{1}{2}\pi (r)^2 = 4\pi r^2.

 

Therefore, the shaded region occupies

\frac{4\pi r^2}{12.5\pi r^2} = 32\%

of the total area of the logo.

Link Problem
Problem 24 Easy

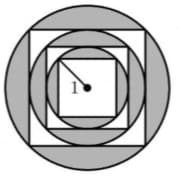
Some squares are inscribed in a set of concentric circles, as shown in the figure. Given that the radius of the smallest circle is 1cm, what is the area of the shaded part in square centimeters? (Take \pi = \frac{22}{7})

  • A.

    6

  • B.

    8

  • C.

    9

  • D.

    \frac{78}{7}

  • E.

    12

Answer:B

We calculate the area of the shaded part by dividing it into three parts:

the inner circle, the middle circle, and the outer circle.

the inner shaded area = the area of the inner circle - the area of the inner square:

\pi \times 1^2 - \left(\frac{2 \times 2}{2}\right) = \pi - 2 \quad (cm^{2})

The diameter of the inner circle is the side length of the middle square, which is 2cm. The diagonal of the middle square is the diameter of the middle circle.

Thus, the area of the middle shaded part is:

\pi \times \left(\frac{\sqrt{2^2 + 2^2}}{2}\right)^2 - (2 \times 2) = \pi \times 2 - 4 = 2\pi - 4 \quad (cm^{2}).

The area of the outer square is equal to the square of the diameter of the middle circle, which is 8cm^{2}. The square of the diagonal of the outer square is twice its area, so it is 16 cm², which equals the square of the diameter of the outer circle.

Thus, the area of the outer shaded part is:

\pi \times \left(\frac{\sqrt{16}}{2}\right)^2 - 8 = \pi \times 4 - 8 = 4\pi - 8 \quad (cm^{2})

Adding up the three parts, the total area of the shaded part is: (\pi - 2) + (2\pi - 4) + (4\pi - 8) = 7\pi - 14

Substituting \pi = \frac{22}{7}:

7 \times \frac{22}{7} - 14 = 22 - 14 = 8 \quad (cm^{2})

Answer: The area of the shaded part is 8cm^{2}.

Link Problem
Problem 25 Easy

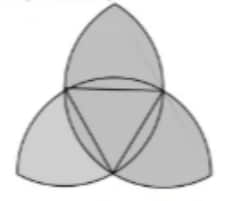
With each of the three vertices of an equilateral triangle with a side length of 2 centimeters as the center, arcs are drawn with a radius of 2 centimeters. What is the perimeter of the shaded figure in centimeters? (Take \pi = 3.14)

  • A.

    3.14

  • B.

    6.28

  • C.

    9.42

  • D.

    12.56

  • E.

    15.7

Answer:D

Each arc is \frac{1}{6} of the circumference of a circle because the central angle of each arc is 60^\circ.

Therefore, the perimeter of the shaded figure is composed of 6 such arcs.

The length of one arc is: \frac{1}{6} \times 2\pi r = \frac{1}{6} \times 2 \times 3.14 \times 2

The total perimeter of the shaded figure is: 6 \times \left( \frac{1}{6} \times 2 \times 3.14 \times 2 \right) = 2 \times 3.14 \times 2 = 12.56 \text{ centimeters}

Thus, the perimeter of the shaded figure is \boxed{12.56} centimeters.

Link Problem
Problem 26 Easy

Andy and Emily start from the same location. Andy walks 5 meters west, and Emily walks 12 meters south. Then Andy walks 3 meters north, and Emily walks 3 meters east. How far apart are they at this point?

  • A.

    15 m

  • B.

    \sqrt{269}m

  • C.

    17 m

  • D.

    20m

  • E.

    23 m

Answer:C

We draw a diagram.

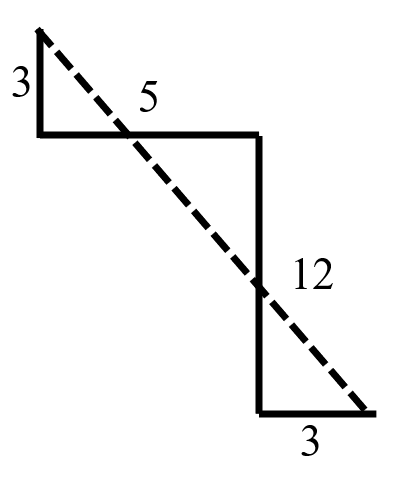
The distance between them is: \sqrt{(3 + 12)^2 + (5 + 3)^2} = \sqrt{15^2 + 8^2} = \sqrt{225 + 64} = \sqrt{289} = 17 \text{ meters}

Link Problem
Problem 27 Easy

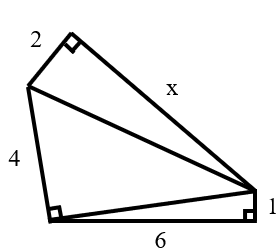
The figure below consists of three right triangles. What is the value of x?

  • A.

    4\sqrt{2}

  • B.

    6

  • C.

    7

  • D.

    \sqrt{57}

  • E.

    8

Answer:C

Since all three triangles in the figure are right triangles, we apply the Pythagorean theorem: x^2 = (1^2 + 6^2 + 4^2) - 2^2

x^2 = 49

x = 7

Link Problem
Problem 28 Easy

What is the length of BE?

  • A.

    10

  • B.

    11

  • C.

    12

  • D.

    13

  • E.

    14

Answer:D

Draw a perpendicular line from point B to FE, with the intersection point being G.

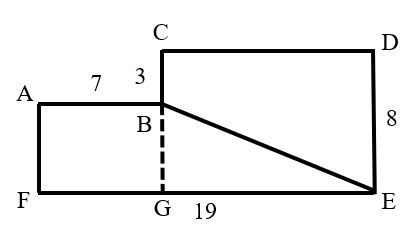
Then: BG = DE - BC = 5, EG = FE - AB = 12.

Since \triangle BGE is a right triangle, by the Pythagorean theorem:

BE = \sqrt{BG^2 + GE^2} = 13.

Link Problem
Problem 29 Easy

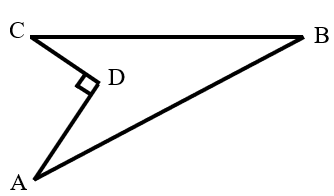
As shown in the figure, there is a lawn. It is known that AD = 12m, CD = 9m, AB = 39m, BC = 36m, and \angle ADC = 90^\circ. Find the area of this lawn.

  • A.

    160

  • B.

    189

  • C.

    216

  • D.

    245

  • E.

    270

Answer:C

Connect AC.

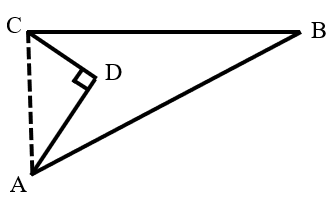
Since \angle ADC = 90^\circ, in the right triangle ACD: AC = \sqrt{DA^2 + DC^2} = 15 m.

Given AB = 39m and BC = 36m, we find that BC^2 + AC^2 = AB^2, so \triangle ABC is also a right triangle.

The area of the lawn is: \text{Area of } \triangle ABC - \text{Area of } \triangle ACD = \frac{1}{2} \times 36 \times 15 - \frac{1}{2} \times 12 \times 9 = 270 - 54 = 216 \text{ square meters}

Link Problem
Problem 30 Easy

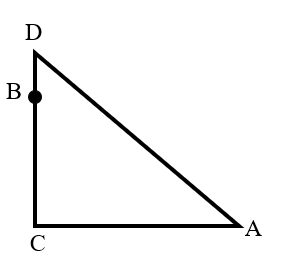
As shown in the figure, there are two monkeys at point B, which is 10 meters high on a tree. One monkey climbs down the tree to reach point A (a pond 20 meters away from the tree), and the other climbs to the top D of the tree and then jumps directly to A. The distance of the jump is calculated as a straight line. If the distances traveled by the two monkeys are equal, what is the height of the tree in meters?

  • A.

    15

  • B.

    16

  • C.

    17

  • D.

    18

  • E.

    19

Answer:A

Let DB = h.

In the right triangle DCA: DA = \sqrt{DC^2 + CA^2} = \sqrt{(h + 10)^2 + 20^2}.

Since the distances traveled by the two monkeys are equal:

DB + DA = BC + CA

h + \sqrt{(h + 10)^2 + 20^2} = 30

\sqrt{(h + 10)^2 + 20^2} = 30 - h

Solving this equation gives h = 5.

Thus, the height of the tree is 10 + 5 = 15 meters.

Link Problem
Related Paper
AMC 8 Daily Practice Round 9 AMC 8 Daily Practice Round 8 AMC 8 Daily Practice Round 6 AMC 8 Daily Practice - Pythagorean Theorem
Table of Contents
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
Think Academy Powered by ChatGPT