AMC 8 Daily Practice Round 6

Complete problem set with solutions and individual problem pages

Problem 1 Easy

What is the value of (7 + 8 + 9) - 7 + (7 + 8 + 9) - 8 + (7 + 8 + 9) - 9?

  • A.

    -24

  • B.

    24

  • C.

    48

  • D.

    72

  • E.

    96

Answer:C

Through observation, we notice that the expression (7 + 8 + 9) appears repeatedly in the original formula.

The expression can be rewritten as: (7 + 8 + 9) - 7 + (7 + 8 + 9) - 8 + (7 + 8 + 9) - 9 = (7 + 8 + 9) + (7 + 8 + 9) + (7 + 8 + 9) - 7 - 8 - 9 = 3 \times (7 + 8 + 9) - (7 + 8 + 9) = (7 + 8 + 9) \times (3 - 1) = (7 + 8 + 9) \times 2 = 24 \times 2 = 48

Thus, the final result is \boxed{48}.

Link Problem
Problem 2 Easy

What is the value of 211\times 555+445\times 789+555\times 789+211\times 445?

  • A.

    999999

  • B.

    1000000

  • C.

    936840

  • D.

    1111111

  • E.

    100000

Answer:B

Method 1:

By observation, we notice that the expression contains common factors 211 and 789.

Applying the associative property of multiplication, the original expression can be rewritten as: 211 \times 555 + 445 \times 789 + 555 \times 789 + 211 \times 445 = 211 \times (555 + 445) + 789 \times (445 + 555) = 211 \times 1000 + 789 \times 1000 = (211 + 789) \times 1000 = 1000 \times 1000 = 1,000,000

Thus, the result is \boxed{1000000}.

Method 2:

By observation, we notice that the expression contains common factors 555 and 445.

Applying the associative property of multiplication, the original expression can be rewritten as: 211 \times 555 + 445 \times 789 + 555 \times 789 + 211 \times 445 = 555 \times (211 + 789) + 445 \times (789 + 211) = (555 + 445) \times (211 + 789) = 1000 \times 1000 = 1,000,000

Thus, the result is \boxed{1000000}.

Link Problem
Problem 3 Medium

What is the value of 169 - 168 - 167 + 166 + 165 - 164 - 163 + 162 + \dots + 9?

  • A.

    0

  • B.

    -9

  • C.

    5

  • D.

    9

  • E.

    84

Answer:D

By observing the arithmetic expression, we notice that the sum of the first four numbers is 0: 169 - 168 - 167 + 166 = 0

Examining the next set of four numbers, we find their sum is also 0: 165 - 164 - 163 + 162 = 0

Thus, the original expression can be rewritten as: 169 - 168 - 167 + 166 + 165 - 164 - 163 + 162 + \dots + 9 = (169 - 168 - 167 + 166) + (165 - 164 - 163 + 162) + \dots + 9

The problem now reduces to determining how many such groups exist. From 169 to 9, there are a total of 161 numbers.

When divided into groups of four, we get: 161 \div 4 = 40 groups with a remainder of 1.

Therefore, the original expression can be represented as: (169 - 168 - 167 + 166) + (165 - 164 - 163 + 162) + \dots + 9= 40 \times 0 + 9 = 9

The final result is \boxed{9}.

Link Problem
Problem 4 Easy

What is the value of 2025 - 2024 + 2023 - 2022 + 2021 - 2020 + 2019 - 2018 + \dots + 3 - 2 + 1?

  • A.

    1012

  • B.

    1013

  • C.

    1014

  • D.

    1015

  • E.

    1016

Answer:B

By observing the arithmetic sequence, we notice that the sum of every two consecutive numbers from left to right is 1.

Therefore, we can group the numbers in pairs. Since there are 2025 numbers in total, dividing them into groups of two yields: 2025 \div 2 = 1012 groups with a remainder of 1.

Thus, the original expression can be rewritten as: 2025 - 2024 + 2023 - 2022 + 2021 - 2020 + 2019 - 2018 + \dots + 3 - 2 + 1 = (2025 - 2024) + (2023 - 2022) + (2021 - 2020) + (2019 - 2018) + \dots + (3 - 2) + 1 = \underbrace{1 + 1 + 1 + \dots + 1}_{1012 \text{ terms}} + 1 = 1 \times 1012 + 1 = 1013

The final result is \boxed{1013}.

Link Problem
Problem 5 Easy

What is the value of 4 - 6 + 8 - 10 + \dots + 2020 - 2022 + 2024?

  • A.

    1014

  • B.

    1010

  • C.

    -1010

  • D.

    1016

  • E.

    1018

Answer:A

Through observation, we find that the sum of every two consecutive numbers is -2.

Grouping the sequence into pairs, we calculate the total number of terms as: 2024 \div 2 - 1 = 1011 numbers, 1011 \div 2 = 505\dots1 which forms 505 complete groups with 1 remaining term.

The original expression can thus be rewritten as: 4 - 6 + 8 - 10 + \dots + 2020 - 2022 + 2024 = (4 - 6) + (8 - 10) + \dots + (2020 - 2022) + 2024 = \underbrace{(-2) + (-2) + \dots + (-2)}_{505 \text{ terms}} + 2024 = (-2) \times 505 + 2024 = -1010 + 2024 = 1014.

The final result is \boxed{1014}.

Link Problem
Problem 6 Easy

What is the value of 1 \frac{1}{2} \times 1 \frac{1}{3} \times 1 \frac{1}{4} \times 1 \frac{1}{5} \times 1 \frac{1}{6} \times 1 \frac{1}{7} \times 1 \frac{1}{8} \times 1 \frac{1}{9}?

  • A.

    1

  • B.

    \frac{1}{5}

  • C.

    5

  • D.

    \frac{5}{9}

  • E.

    10

Answer:C

The problem involves mixed numbers.

We first convert each mixed number to an improper fraction:

1\frac{1}{2} \times 1\frac{1}{3} \times 1\frac{1}{4} \times 1\frac{1}{5} \times 1\frac{1}{6} \times 1\frac{1}{7} \times 1\frac{1}{8} \times 1\frac{1}{9}= \frac{3}{2} \times \frac{4}{3} \times \frac{5}{4} \times \frac{6}{5} \times \frac{7}{6} \times \frac{8}{7} \times \frac{9}{8} \times \frac{10}{9}= \frac{\not{3}}{2} \times \frac{\not{4}}{\not{3}} \times \frac{\not{5}}{\not{4}} \times \frac{\not{6}}{\not{5}} \times \frac{\not{7}}{\not{6}} \times \frac{\not{8}}{\not{7}} \times \frac{\not{9}}{\not{8}} \times \frac{10}{\not{9}}=\frac{1}{2} \times \frac{10}{1} = 5

Final result:\boxed{5}

Link Problem
Problem 7 Easy

What is the value of \frac{1}{2} \times\left(1-\frac{1}{3}\right) \times\left(1-\frac{1}{4}\right) \times \cdots \times\left(1-\frac{1}{100}\right)?

  • A.

    \frac{1}{100}

  • B.

    \frac{1}{2}

  • C.

    \frac{1}{3}

  • D.

    \frac{1}{4}

  • E.

    \frac{1}{99}

Answer:A

First, we calculate the value inside each parenthesis, so the original expression can be rewritten as: \frac{1}{2} \times \left(1 - \frac{1}{3}\right) \times \left(1 - \frac{1}{4}\right) \times \cdots \times \left(1 - \frac{1}{100}\right)=\frac{1}{2} \times \frac{2}{3} \times \frac{3}{4} \times \cdots \times \frac{99}{100}

We observe a telescoping pattern where the denominator of each fraction cancels with the numerator of the subsequent fraction: \frac{1}{\not{2}} \times \frac{\not{2}}{\not{3}} \times \frac{\not{3}}{\not{4}} \times \cdots \times \frac{\not{99}}{100}

After complete cancellation of adjacent terms, only the first numerator and the last denominator remain: = \frac{1}{100}

Final result: \boxed{\frac{1}{100}}

Link Problem
Problem 8 Easy

What is the value of \frac{3}{4} \times \frac{8}{9} \times \frac{15}{16} \times \frac{24}{25} \times \frac{35}{36} \times \frac{48}{49}?

  • A.

    \frac{3}{4}

  • B.

    \frac{8}{25}

  • C.

    \frac{1}{2}

  • D.

    \frac{4}{7}

  • E.

    \frac{48}{49}

Answer:D

By observation, we notice that all denominators are perfect squares.

We can attempt the following transformation: \frac{3}{4} \times \frac{8}{9} \times \frac{15}{16} \times \frac{24}{25} \times \frac{35}{36} \times \frac{48}{49}=\frac{1 \times 3}{2 \times 2} \times \frac{2 \times 4}{3 \times 3} \times \frac{3 \times 5}{4 \times 4} \times \frac{4 \times 6}{5 \times 5} \times \frac{5 \times 7}{6 \times 6} \times \frac{6 \times 8}{7 \times 7} = \frac{1}{2} \times \frac{3}{2} \times \frac{2}{3} \times \frac{4}{3} \times \frac{3}{4} \times \frac{5}{4} \times \frac{4}{5} \times \frac{6}{5} \times \frac{5}{6} \times \frac{7}{6} \times \frac{6}{7} \times \frac{8}{7}

Now we group terms to make the cancellation explicit: = \frac{1}{2} \times \left(\frac{3}{2} \times \frac{2}{3}\right) \times \left(\frac{4}{3} \times \frac{3}{4}\right) \times \left(\frac{5}{4} \times \frac{4}{5}\right) \times \left(\frac{6}{5} \times \frac{5}{6}\right) \times \left(\frac{7}{6} \times \frac{6}{7}\right) \times \frac{8}{7}

Each pair in parentheses cancels out completely: = \frac{1}{2} \times 1 \times 1 \times 1 \times 1 \times 1 \times \frac{8}{7}

After all cancellations, we are left with: = \frac{1}{2} \times \frac{8}{7} = \frac{4}{7}

Final result: \boxed{\frac{4}{7}}

Link Problem
Problem 9 Easy

What id the value of \left(1-\frac{1}{2}\right) \times\left(2-\frac{2}{3}\right) \times\left(3-\frac{3}{4}\right) \times \cdots \times\left(8-\frac{8}{9}\right) \times\left(9-\frac{9}{10}\right)?

  • A.

    \frac{1}{2}

  • B.

    \frac{1}{3}

  • C.

    \frac{1}{10}

  • D.

    362880

  • E.

    36288

Answer:E

 Observing the expression, we notice repeated numbers in each parenthesis.

Factoring out these common terms, we can rewrite the expression as:   1 \times\left(1-\frac{1}{2}\right) \times 2 \times \left(1-\frac{1}{3}\right) \times 3 \times \left(1-\frac{1}{4}\right) \times \cdots \times 8 \times \left(1-\frac{1}{9}\right) \times 9 \times \left(1-\frac{1}{10}\right)

Rearranging the terms by moving the constants to the left and the fractions to the right, we get:   [1 \times 2 \times 3 \times \cdots \times 9] \times \left[\left(1-\frac{1}{2}\right) \times \left(1-\frac{1}{3}\right) \times \cdots \times \left(1-\frac{1}{10}\right)\right]

The right part of the expression is a telescoping product:   \left(\frac{1}{2}\right) \times \left(\frac{2}{3}\right) \times \left(\frac{3}{4}\right) \times \cdots \times \left(\frac{9}{10}\right) = \frac{1}{\not{2}} \times \frac{\not{2}}{\not{3}} \times \frac{\not{3}}{\not{4}} \times \cdots \times \frac{\not{9}}{10} = \frac{1}{10}

Therefore, the original expression simplifies to:   9! \times \frac{1}{10} = \frac{9!}{10} = \frac{362880}{10} = 36288

Final result: \boxed{36288}

Link Problem
Problem 10 Easy

What is the value of \frac{2^{2}}{3^{2}-1} \times \frac{4^{2}}{5^{2}-1} \times \frac{6^{2}}{7^{2}-1} \times \cdots \times \frac{20^{2}}{21^{2}-1}?

  • A.

    \frac{1}{8}

  • B.

    \frac{1}{11}

  • C.

    \frac{1}{20}

  • D.

    \frac{1}{2}

  • E.

    \frac{1}{441}

Answer:B

By observing the expression, we notice that the denominators can be factored using the difference of squares formula (a^2 - b^2) = (a-b)(a+b).

Let's rewrite the expression accordingly:   \frac{2^{2}}{3^{2}-1} \times \frac{4^{2}}{5^{2}-1} \times \frac{6^{2}}{7^{2}-1} \times \cdots \times \frac{20^{2}}{21^{2}-1} = \frac{2^{2}}{(3-1)(3+1)} \times \frac{4^{2}}{(5-1)(5+1)} \times \frac{6^{2}}{(7-1)(7+1)} \times \cdots \times \frac{20^{2}}{(21-1)(21+1)} = \frac{2 \times 2}{2 \times 4} \times \frac{4 \times 4}{4 \times 6} \times \frac{6 \times 6}{6 \times 8} \times \cdots \times \frac{20 \times 20}{20 \times 22}

Now we can see a clear cancellation pattern emerging : = \frac{\not{2} \times 2}{\not{2} \times 4} \times \frac{\not{4} \times 4}{\not{4} \times 6} \times \frac{\not{6} \times 6}{\not{6} \times 8} \times \cdots \times \frac{\not{20} \times 20}{\not{20} \times 22}

After complete cancellation of common factors, we are left with:   = \frac{2}{4} \times \frac{4}{6} \times \frac{6}{8} \times \cdots \times \frac{20}{22}

Observing this telescoping product, we see that each numerator cancels with the denominator of the next fraction:   = \frac{2}{\not{4}} \times \frac{\not{4}}{\not{6}} \times \frac{\not{6}}{\not{8}} \times \cdots \times \frac{\not{20}}{22}

After all cancellations, only the first numerator and the last denominator remain:   = \frac{2}{22} = \frac{1}{11}

Final result: \boxed{\frac{1}{11}}

Link Problem
Problem 11 Easy

Consider the following operation: a\oplus b=a-b^{2}. What is the value of  4 \oplus[5 \oplus(-2)]?

  • A.

    2

  • B.

    3

  • C.

    4

  • D.

    5

  • E.

    -2

Answer:B

According to the problem, a new operation is defined as a \oplus b = a - b^2.

To evaluate 4 \oplus [5 \oplus (-2)], we should firstly calculate the inner operation:    5 \oplus (-2) = 5 - (-2)^2= 5 - (4)= 1

Now substitute this result into the outer operation:    4 \oplus [5 \oplus (-2)] = 4 \oplus 1= 4 - (1)^2= 4 - 1= 3

Final result is \boxed{3}

Link Problem
Problem 12 Easy

Consider these two operations: 2 \# 4=2+2.5+3+3.5, 5 \# 3=5+5.5+6. What is the value of  10 \# 5?

  • A.

    10

  • B.

    12

  • C.

    55

  • D.

    50

  • E.

    15

Answer:C

The problem defines a custom operator \# such that:

2 \# 4 = 2 + 2.5 + 3 + 3.5   5 \# 3 = 5 + 5.5 + 6

By observing these examples:

The first number on the left side of = becomes the starting number of the sequence on the right side.

The second number on the left side of = indicates the number of terms in the sequence on the right side.

The sequence forms an arithmetic progression with a common difference of 0.5.

Therefore, for 10 \# 5=10 + 10.5 + 11 + 11.5 + 12 = 55

The value of 10 \# 5 is \boxed{55}

Link Problem
Problem 13 Easy

Define the operation A \otimes B = \frac{KA - B}{2}. Given that 5 \otimes 3 = 11, find the value of K.

  • A.

    3

  • B.

    4

  • C.

    5

  • D.

    8

  • E.

    11

Answer:C

Substitute A = 5 and B = 3 into the definition of \otimes:   5 \otimes 3 = \frac{K \cdot 5 - 3}{2} = 11

Multiply both sides by 2 to eliminate the denominator:   K \cdot 5 - 3 = 22

Add 3 to both sides:   K \cdot 5 = 25

Divide both sides by 5:   K = 5

Final Answer:  \boxed{5}

Link Problem
Problem 14 Easy

Let a and b be rational numbers. Define the operations:  a * b = \sqrt[3]{a} - \sqrt{b},  a \land b = a^{2} - b^{2}.

Compute (-1) \land (8 * 16).

  • A.

    -1

  • B.

    -2

  • C.

    -3

  • D.

    -4

  • E.

    -6

Answer:C

First, compute 8 * 16 using the first operation rule: 8 * 16 = \sqrt[3]{8} - \sqrt{16} = 2 - 4 = -2

Next, compute (-1) \land (-2) using the second operation rule: (-1) \land (-2) = (-1)^{2} - (-2)^{2} = 1 - 4 = -3

Final Answer:   \boxed{-3}

Link Problem
Problem 15 Easy

For two natural numbers a and b, their least common multiple (LCM) minus their greatest common divisor (GCD) is defined as a \pm b,  a \pm b = [a, b] - (a, b). What is the value of  125 \pm 25?

  • A.

    0

  • B.

    25

  • C.

    50

  • D.

    100

  • E.

    125

Answer:D

1. Compute the GCD of 125 and 25:      (125, 25) = 25

2. Compute the LCM of 125 and 25:      [125, 25] = 125

3. Subtract the GCD from the LCM:      125 \pm 25 = [125, 25] - (125, 25) = 125 - 25 = 100

Final Answer:  \boxed{100}

Link Problem
Problem 16 Easy

Halley's Comet has been observed passing by Earth in the years 1682, 1758, 1834, 1910, and 1986. Based on the pattern, when might it return in this century?

  • A.

    2000

  • B.

    2025

  • C.

    2037

  • D.

    2062

  • E.

    2076

Answer:D

Observing the years forms an arithmetic sequence with the first term 1682 and a common difference 76.

The next return year would be: 1986 + 76 = 2062

Final result: \boxed{2062}

Link Problem
Problem 17 Easy

John plans to train for a 5000m race with a 15-day program: 5000m on Day 1, increasing by 300m daily. How far will he run on Day 15?

  • A.

    4700m

  • B.

    7400m

  • C.

    8000m

  • D.

    9200m

  • E.

    9500m

Answer:D

This forms an arithmetic sequence with a_1 = 5000 and d = 300.

Using the nth-term formula: a_{15} = 5000 + 300 \times (15-1) = 5000 + 4200 = 9200m

Final result: \boxed{9200} meters

Link Problem
Problem 18 Easy

A 5-shelf bookcase holds 450 books. Each upper shelf has 10 fewer books than the one below. How many books on the top shelf?

  • A.

    10

  • B.

    70

  • C.

    90

  • D.

    200

  • E.

    450

Answer:B

Let shelves be 1 (top) to 5.

The middle shelf (3rd) has: 450\div5 = 90 books.

Top shelf: 90 - 10 - 10 = 70.

 Final result: \boxed{70} books

Link Problem
Problem 19 Easy

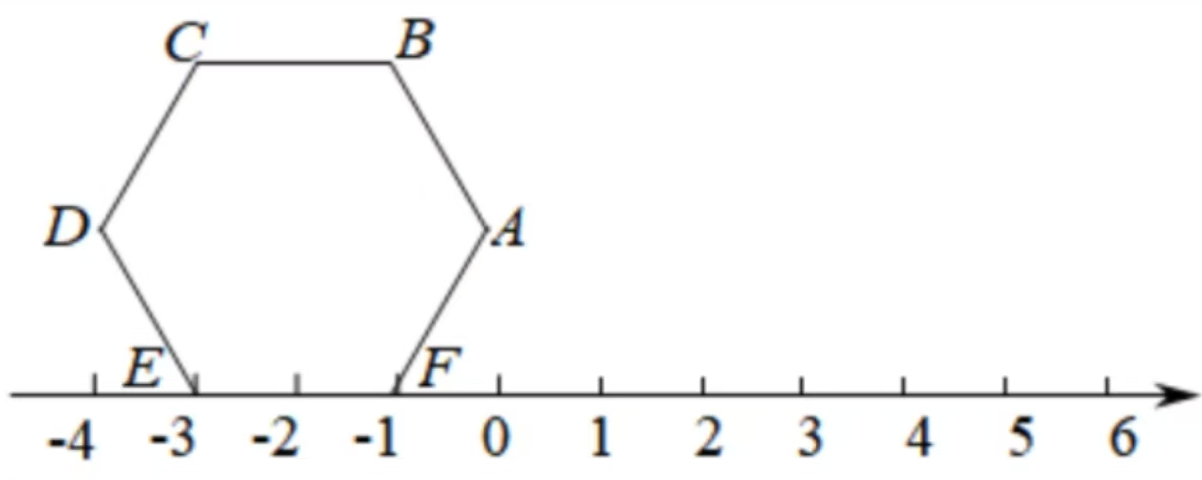
As shown in the diagram, a regular hexagon ABCDEF (with all sides equal) is positioned on a number line. Points E and F correspond to numbers-3 and -1, respectively. When the hexagon is rotated clockwise around a vertex, after 1 rotation, point A aligns with the number 1. Continuing this rotation pattern, identify which vertex of the hexagon corresponds to the number 4041 on the number line.

  • A.

    E

  • B.

    D

  • C.

    C

  • D.

    B

  • E.

    A

Answer:A

From the first rotation, point A moves to 1, indicating the side length of the hexagon is 2 (distance between -1 and 1).

Observing the rotation pattern:

- After 1 rotation: Point A → 1

- After 2 rotations: Point B → 3

- After 3 rotations: Point C → 5

- After 4 rotations: Point D → 7

- After 5 rotations: Point E → 9

- After 6 rotations: Point F → 11

- After 7 rotations: Point A → 13

This establishes a periodic pattern with period 6.

The general formula for the position after n rotations is:

\text{Position} = -1 + 2n

Set -1 + 2n = 4041\Rightarrow \quad2n = 4042 \quad \Rightarrow \quad n = 2021

Determine the position within the 6-rotation cycle:   2021 \div 6 = 336 \text{ remainder } 5

A remainder of 5 corresponds to the 5th vertex in the cycle (E).

Final result: \boxed{E}

Link Problem
Problem 20 Easy

How many integers between 401 and 1000, inclusive, leave a remainder of 1 when divided by 8?

  • A.

    72

  • B.

    73

  • C.

    74

  • D.

    75

  • E.

    76

Answer:D

These integers form an arithmetic sequence with first term 1, common difference 8, and general term 8n-7.

Within the range 401–1000:

The smallest term is 401 (when n=51: 8 \times 51 - 7 = 401).

The largest term is 993 (when n=125: 8 \times 125 - 7 = 993).

The number of terms is calculated as: \frac{993 - 401}{8} + 1 = \frac{592}{8} + 1 = 74 + 1 = 75

Final result: \boxed{75}

Link Problem
Problem 21 Easy

A town hall clock chimes the hour number on every full hour and once on every half-hour. How many chimes will occur in a full 24-hour period?

  • A.

    24

  • B.

    90

  • C.

    156

  • D.

    180

  • E.

    270

Answer:D

Daily chimes:   2 \times \left(1+2+3+\cdots+12+ 12 \right) = 2 \times \left( \frac{12 \times \left(1+12\right)}{2} + 12 \right) = 180

Link Problem
Problem 22 Easy

Four campers—Alice, Bob, Charlie, and Diana—play a number-reporting game around a campfire. In Round 1, Alice reports 1, Bob reports 2 and 3, Charlie reports 4, 5, 6, and Diana reports 7, 8, 9, 10. In Round 2, Alice continues with 11 through 15, maintaining the same pattern. How many numbers did Alice report in the first five rounds?

  • A.

    13

  • B.

    17

  • C.

    30

  • D.

    45

  • E.

    50

Answer:D

Alice's reporting pattern follows an arithmetic sequence where the number of terms per round increases by 4 each time: 1, 5, 9, 13, 17 terms for Rounds 1 to 5.

Using the arithmetic series sum formula:

1+5+9+13+17= \frac{(1+17)\times5}{2}=45

Final result: \boxed{45}

Link Problem
Problem 23 Medium

37 students line up to count consecutively starting at 1, with each subsequent number increasing by 3. One student erroneously subtracts 3 instead, resulting in a total sum of 2011. Which student made the counting error?

  • A.

    32

  • B.

    33

  • C.

    34

  • D.

    35

  • E.

    36

Answer:C

If all students counted correctly, the sequence forms an arithmetic progression with: First term a_1 = 1, Common difference d = 3 ，37^{\text{th}} term:   a_{37} = a_1 + d(n-1) = 1 + 3 \times (37-1) = 109.

The correct sequence would be 1, 4, 7, 10, \dots, 109. The total sum is: S_{37} = \frac{(a_1 + a_{37}) \times 37}{2} = \frac{(1 + 109) \times 37}{2} = 2035

The discrepancy between the correct sum and actual sum is: 2035 - 2011 = 24

Starting from the erroneous student, each subsequent student's number is 6 less than expected.

The number of affected terms is: \frac{24}{6} = 4

Thus, the error occurs at position: 34

Final result: \boxed{34}

Link Problem
Problem 24 Easy

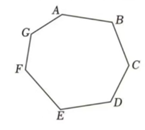
A game piece starts at vertex A of a heptagon board labeled A, B, C, D, E, F, G clockwise. Players move the piece 10 times following this rule: on the k-th move, jump k vertices clockwise. Which vertices remain unvisited after 10 moves?

  • A.

    C, E, and F

  • B.

    E, F

  • C.

    C, E

  • D.

    B,C and F

  • E.

    C, F

Answer:A

Label the vertices as 0 (A), 1 (B), 2 (C), 3 (D), 4 (E), 5 (F), and 6 (G).  

After k moves, the total number of positions traversed is:   S_k = \frac{k(k+1)}{2}  

The final position is determined by computing the remainder Z when S_k is divided by 7:   Z = S_k \bmod 7  

By calculating Z for k=1, 2, \dots, 10, we observe the repeating sequence of remainders:   1, 3, 6, 3, 1, 0, 0, 1, 3, 6.  

Vertices corresponding to remainders 2, 4, and 5 (i.e., C, E, and F) are never visited.  

Final result: \boxed{\text{C, E, and F}}

Link Problem
Problem 25 Medium

A retirement community has 20 residents with integer ages summing to 1520. The oldest resident is aged >90 but \leq 100, while the remaining 19 residents have consecutive ages. What is the age range of the community?

  • A.

    19

  • B.

    29

  • C.

    30

  • D.

    66

  • E.

    95

Answer:B

Let minimum age be n. The sequence is: \underbrace{n, n+1, \dots, n+18}_{19 \text{ terms}}, \quad m

Sum equation: \frac{19}{2}(2n + 18) + m = 1520 \implies 19n + 171 + m = 1520 \implies m = 1349 - 19n

Given 90 < m \leq 100, solve: 90 < 1349 - 19n \leq 100 \implies 65.7 \leq n < 66.3 \implies n = 66

Thus m = 95, and age range = 95 - 66 = 29.

Final result: \boxed{29}

Link Problem
Problem 26 Easy

The average of five consecutive odd numbers is 1997. What is the value of the square of the largest number minus the square of the smallest number?

  • A.

    15976

  • B.

    19432

  • C.

    21432

  • D.

    23976

  • E.

    31952

Answer:E

5 odd numbers: 1993, 1995, 1997, 1999 and 2001.

{{2001}^{2}}-{{1993}^{2}}=\left( 2001+1993 \right)\left( 2001-1993 \right)=3994\times 8=31952.

Link Problem
Problem 27 Easy

What is the value of 9999^2 + 19999？

  • A.

    100000000

  • B.

    19999998

  • C.

    9999

  • D.

    199999999

  • E.

    99999999

Answer:A

9999^2 + 19999 = 9999^2 + 9999 \times 2 + 1= 9999^2 + 2 \times 9999 \times 1 + 1^2= (9999 + 1)^2 = 10000^2= 100000000

Final result:  \boxed{100000000}

Link Problem
Problem 28 Easy

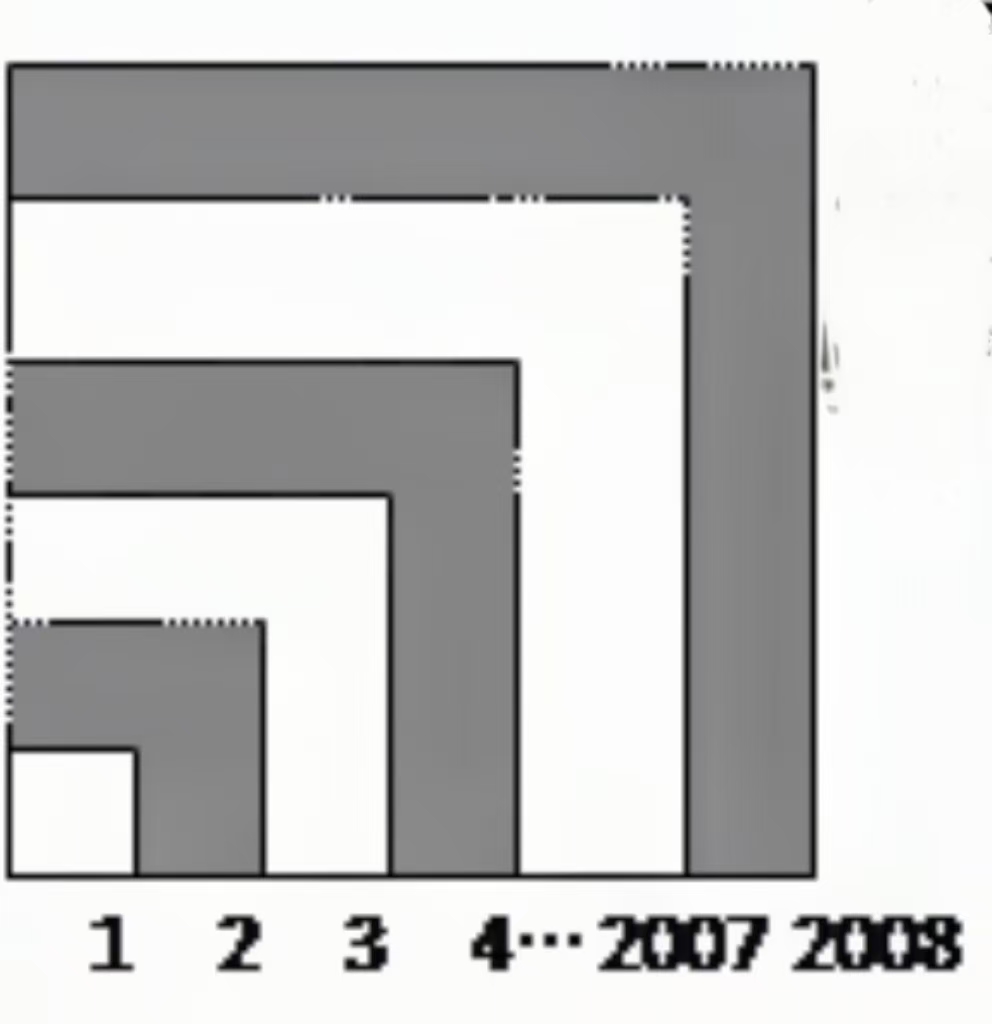
Calculate the shaded area formed by overlapping squares with side lengths 1, 2, 3, \ldots, 2008.

  • A.

    2008000

  • B.

    2009000

  • C.

    2017036

  • D.

    1000000

  • E.

    2007000

Answer:C

The shaded area is the alternating sum of squares:

(2^2-1^2) + (4^2-3^2) + \cdots + (2008^2-2007^2) \\

= (2+1)(2-1) + (4+3)(4-3) + \cdots + (2008+2007)(2008-2007) \\

= 1 + 2 + 3 + \cdots + 2008 \\

= \frac{2008 \times (1+2008)}{2} = 2017036

Final result: \boxed{2017036}

Link Problem
Problem 29 Easy

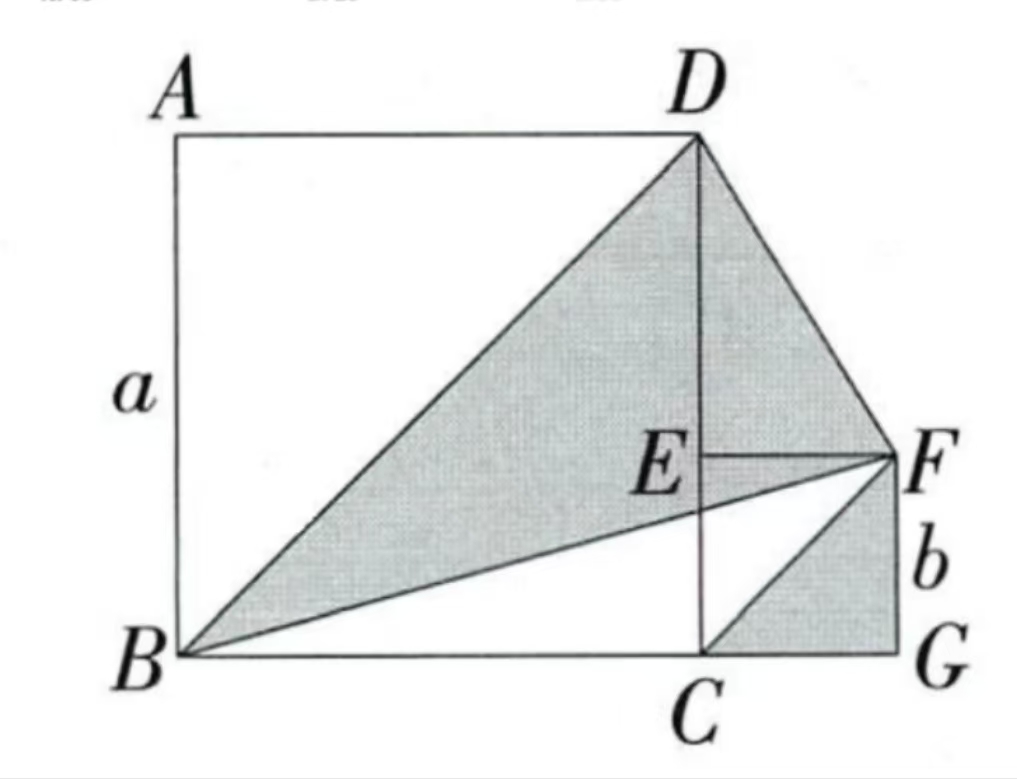
Two squares with sides a and b satisfy a+b=10 and ab=20.Find the shaded area.

  • A.

    20

  • B.

    30

  • C.

    40

  • D.

    45

  • E.

    60

Answer:B

Shaded area

A = \frac{1}{2}a^2 + \frac{1}{2}b(a+b) - \frac{1}{2}ab = \frac{1}{2}(a^2 + b^2).

From (a+b)^2 = a^2 + 2ab + b^2 = 100 \implies a^2 + b^2 = 100 - 40 = 60

Therefore A = \frac{1}{2} \times 60 = 30

Final result: \boxed{30}

Link Problem
Problem 30 Easy

The number 2^{48}-1 is divisible by two integers between 60 and 70. What are these integers?

  • A.

    63,65

  • B.

    63,64

  • C.

    64,65

  • D.

    65,66

  • E.

    67,68

Answer:A

2^{48}-1 = (2^{24}-1)(2^{24}+1) \\

= (2^{12}-1)(2^{12}+1)(2^{24}+1) \\

= (2^6-1)(2^6+1)(2^{12}+1)(2^{24}+1) \\

= 63 \times 65 \times (2^{12}+1)(2^{24}+1)

The factors between 60-70 are 63 and 65.

Final results: \boxed{63,65}

Link Problem
Related Paper
AMC 8 Daily Practice Round 8 AMC 8 Daily Practice Round 7 AMC 8 Daily Practice - Pythagorean Theorem AMC 8 Daily Practice - Circles
Table of Contents
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
Think Academy Powered by ChatGPT