AMC 8 Daily Practice - Pythagorean Theorem

Complete problem set with solutions and individual problem pages

Problem 1 Easy

Andy and Emily start from the same location. Andy walks 5 meters west, and Emily walks 12 meters south. Then Andy walks 3 meters north, and Emily walks 3 meters east. How far apart are they at this point?

  • A.

    15 m

  • B.

    \sqrt{269}m

  • C.

    17 m

  • D.

    20m

  • E.

    23 m

Answer:C

We draw a diagram.

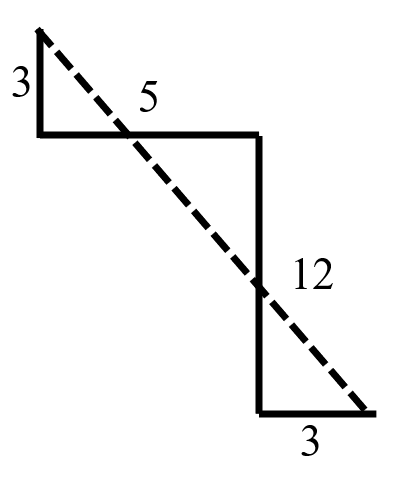
The distance between them is: \sqrt{(3 + 12)^2 + (5 + 3)^2} = \sqrt{15^2 + 8^2} = \sqrt{225 + 64} = \sqrt{289} = 17 \text{ meters}

Link Problem
Problem 2 Easy

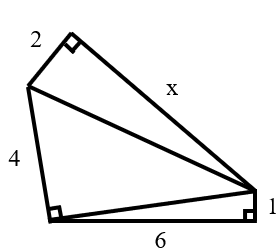
The figure below consists of three right triangles. What is the value of x?

  • A.

    4\sqrt{2}

  • B.

    6

  • C.

    7

  • D.

    \sqrt{57}

  • E.

    8

Answer:C

Since all three triangles in the figure are right triangles, we apply the Pythagorean theorem: x^2 = (1^2 + 6^2 + 4^2) - 2^2

x^2 = 49

x = 7

Link Problem
Problem 3 Easy

What is the length of BE?

  • A.

    10

  • B.

    11

  • C.

    12

  • D.

    13

  • E.

    14

Answer:D

Draw a perpendicular line from point B to FE, with the intersection point being G.

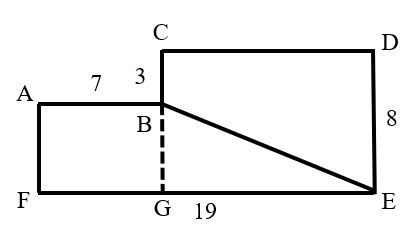
Then: BG = DE - BC = 5, EG = FE - AB = 12.

Since \triangle BGE is a right triangle, by the Pythagorean theorem:

BE = \sqrt{BG^2 + GE^2} = 13.

Link Problem
Problem 4 Easy

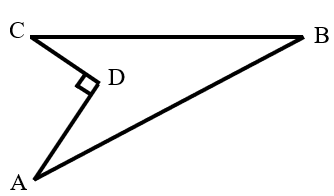
As shown in the figure, there is a lawn. It is known that AD = 12m, CD = 9m, AB = 39m, BC = 36m, and \angle ADC = 90^\circ. Find the area of this lawn.

  • A.

    160

  • B.

    189

  • C.

    216

  • D.

    245

  • E.

    270

Answer:C

Connect AC.

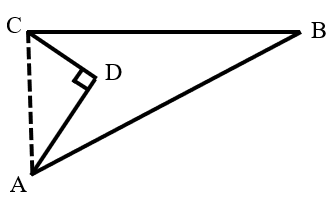
Since \angle ADC = 90^\circ, in the right triangle ACD: AC = \sqrt{DA^2 + DC^2} = 15 m.

Given AB = 39m and BC = 36m, we find that BC^2 + AC^2 = AB^2, so \triangle ABC is also a right triangle.

The area of the lawn is: \text{Area of } \triangle ABC - \text{Area of } \triangle ACD = \frac{1}{2} \times 36 \times 15 - \frac{1}{2} \times 12 \times 9 = 270 - 54 = 216 \text{ square meters}

Link Problem
Problem 5 Easy

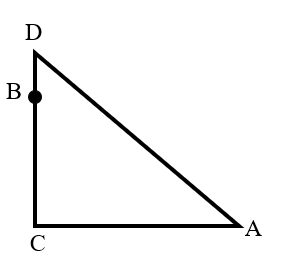
As shown in the figure, there are two monkeys at point B, which is 10 meters high on a tree. One monkey climbs down the tree to reach point A (a pond 20 meters away from the tree), and the other climbs to the top D of the tree and then jumps directly to A. The distance of the jump is calculated as a straight line. If the distances traveled by the two monkeys are equal, what is the height of the tree in meters?

  • A.

    15

  • B.

    16

  • C.

    17

  • D.

    18

  • E.

    19

Answer:A

Let DB = h.

In the right triangle DCA: DA = \sqrt{DC^2 + CA^2} = \sqrt{(h + 10)^2 + 20^2}.

Since the distances traveled by the two monkeys are equal:

DB + DA = BC + CA

h + \sqrt{(h + 10)^2 + 20^2} = 30

\sqrt{(h + 10)^2 + 20^2} = 30 - h

Solving this equation gives h = 5.

Thus, the height of the tree is 10 + 5 = 15 meters.

Link Problem
Problem 6 Easy

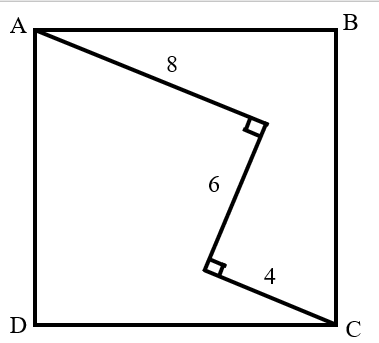
What is the area of square ABCD?

  • A.

    72

  • B.

    80

  • C.

    90

  • D.

    120

  • E.

    180

Answer:C

The area of a square can be calculated as \text{side length} \times \text{side length} or \frac{1}{2} \times \text{diagonal} \times \text{diagonal}.

Connect AC and draw CG \perp AE with G as the foot of the perpendicular.

Quadrilateral CFEG is a rectangle.

In \triangle ACG: AC^2 = AG^2 + CG^2 = 12^2 + 6^2 = 180.

Thus, the area of square ABCD is: \frac{1}{2} \times AC^2 = \frac{1}{2} \times 180 = 90.

Link Problem
Problem 7 Easy

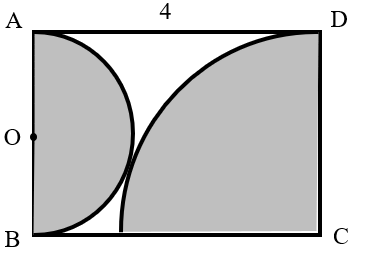
In the rectangle, the arcs of the two sectors are tangent to each other. What is the area of the shaded part?

  • A.

    6\pi

  • B.

    7\pi

  • C.

    8\pi

  • D.

    9\pi

  • E.

    10\pi

Answer:E

As shown in the figure, connect the centers of the semicircle and the sector.

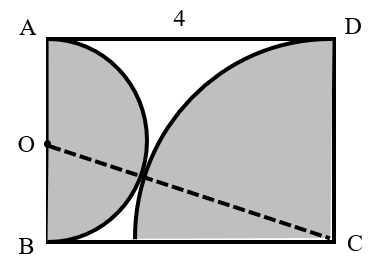
Let the radius of the semicircle be r.

Since AB = DC, the radius of the sector is 2r.

In \triangle OBC, by the Pythagorean theorem:

r^2 + 4^2 = (r + 2r)^2

r^2 + 16 = 9r^2

8r^2 = 16 \implies r^2 = 2

The area of the shaded part is: \pi r^2 + \pi (2r)^2 = \pi r^2 + 4\pi r^2 = 5\pi r^2 = 5\pi \times 2 = 10\pi

Link Problem
Problem 8 Easy

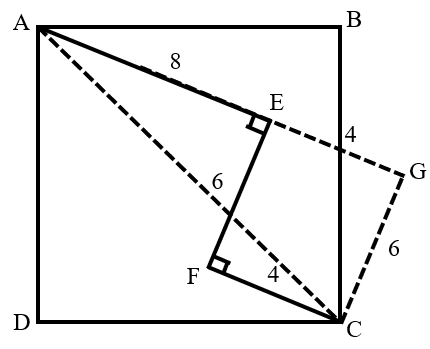
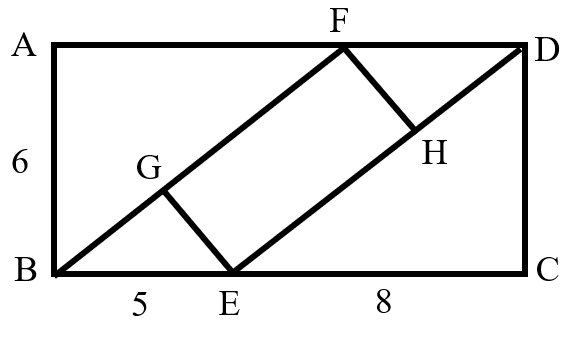
Quadrilateral ABCD is a rectangle. What is the area of the quadrilateral EGFH?

  • A.

    15

  • B.

    16

  • C.

    18

  • D.

    21

  • E.

    24

Answer:C

Given AB = 6 and EC = 8, in \triangle ABF, we find BF = 10.

The area of parallelogram BEDF can be expressed in two ways:

BE \times AB and BF \times EG.

Thus: 5 \times 6 = 10 \times EG

Solving for EG, we get EG = 3.

In the right triangle BGE, by the Pythagorean theorem: BG = \sqrt{BE^2 - EG^2} = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4.

Since GF = 10 - 4 = 6 , the area of the quadrilateral EGFH is: GF \times EG = 6 \times 3 = 18.

Answer: The area of the quadrilateral EGFH is 18 square units.

Link Problem
Related Paper
AMC 8 Daily Practice Round 7 AMC 8 Daily Practice Round 6 AMC 8 Daily Practice - Circles AMC 8 Daily Practice - Solid Figures
Table of Contents
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
Think Academy Powered by ChatGPT