AMC 8 Daily Practice - Circles

Complete problem set with solutions and individual problem pages

Problem 1 Easy

A part of a circular glass mirror is damaged. To obtain a mirror of the same size, a worker uses a right-angle ruler for measurement as shown in the figure, and finds that AB = 12cm and BC = 5cm. What is the diameter of the circular mirror in centimeters?

  • A.

    10

  • B.

    11

  • C.

    12

  • D.

    13

  • E.

    14

Answer:D

It is known that the circumferential angle subtended by a diameter is a right angle.

Therefore, connecting AC forms a right triangle ABC with \angle ABC = 90^\circ, and AC is the diameter of the circular mirror.

By the Pythagorean theorem in \triangle ABC: AC = \sqrt{AB^2 + BC^2} = \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13

Thus, the diameter of the circular mirror is 13 centimeters.

Link Problem
Problem 2 Easy

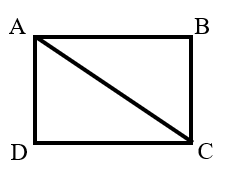
As shown in the figure, ABCD is a rectangle with length 4, width 3, and diagonal length 5. It is rotated 90^\circ clockwise around point C. Find the area swept by side AB.(Take \pi=3.14)

  • A.

    7.065

  • B.

    9.42

  • C.

    12.56

  • D.

    15.7

  • E.

    19.625

Answer:C

The area swept by side AB is the area of the shaded part in the figure.

The area swept by AB = (\text{Area of sector } ACA' + \text{Area of } \triangle A'B'C) -(\text{Area of sector } BCB' + \text{the area of } \triangle ABC).

Since the area of \triangle ABC is equal to the area of \triangle A'B'C, this simplifies to: \text{Area of sector } ACA' - \text{Area of sector } BCB'.

Calculating the areas of the sectors :

= \pi \times 5^2 \times \frac{1}{4} - \pi \times 3^2 \times \frac{1}{4}

= \pi \times 25 \times \frac{1}{4} - \pi \times 9 \times \frac{1}{4}

= \pi \times (25 - 9) \times \frac{1}{4} = \pi \times 16 \times \frac{1}{4}

= 4\pi = 12.56 \quad (\text{taking } \pi \approx 3.14)

Answer: The areas swept by sides AB is 12.56 square units.

Link Problem
Problem 3 Easy

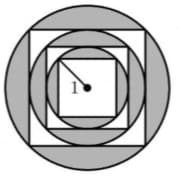
Some squares are inscribed in a set of concentric circles, as shown in the figure. Given that the radius of the smallest circle is 1cm, what is the area of the shaded part in square centimeters? (Take \pi = \frac{22}{7})

  • A.

    6

  • B.

    8

  • C.

    9

  • D.

    \frac{78}{7}

  • E.

    12

Answer:B

We calculate the area of the shaded part by dividing it into three parts:

the inner circle, the middle circle, and the outer circle.

the inner shaded area = the area of the inner circle - the area of the inner square:

\pi \times 1^2 - \left(\frac{2 \times 2}{2}\right) = \pi - 2 \quad (cm^{2})

The diameter of the inner circle is the side length of the middle square, which is 2cm. The diagonal of the middle square is the diameter of the middle circle.

Thus, the area of the middle shaded part is:

\pi \times \left(\frac{\sqrt{2^2 + 2^2}}{2}\right)^2 - (2 \times 2) = \pi \times 2 - 4 = 2\pi - 4 \quad (cm^{2}).

The area of the outer square is equal to the square of the diameter of the middle circle, which is 8cm^{2}. The square of the diagonal of the outer square is twice its area, so it is 16 cm², which equals the square of the diameter of the outer circle.

Thus, the area of the outer shaded part is:

\pi \times \left(\frac{\sqrt{16}}{2}\right)^2 - 8 = \pi \times 4 - 8 = 4\pi - 8 \quad (cm^{2})

Adding up the three parts, the total area of the shaded part is: (\pi - 2) + (2\pi - 4) + (4\pi - 8) = 7\pi - 14

Substituting \pi = \frac{22}{7}:

7 \times \frac{22}{7} - 14 = 22 - 14 = 8 \quad (cm^{2})

Answer: The area of the shaded part is 8cm^{2}.

Link Problem
Problem 4 Easy

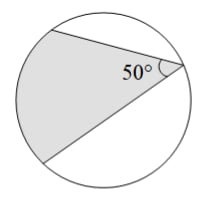
To cultivate students' practical ability, the school's biology interest group set up a circular exhibition hall during the project-based learning "Making a Mini Ecosystem". As shown in the figure, a monitor is installed at point P on the circular edge of the hall, and its monitoring angle is 50^\circ. To observe every position in the exhibition hall, what is the minimum number of such monitors that need to be installed on the circular edge?

  • A.

    2

  • B.

    3

  • C.

    4

  • D.

    5

  • E.

    6

Answer:C

The monitoring angle of the monitor (a circumferential angle) is 50^\circ, so the central angle corresponding to the arc it can monitor is: 50^\circ \times 2 = 100^\circ

To cover the entire circular exhibition hall (with a total central angle of 360^\circ), the minimum number of monitors needed is: 360^\circ \div 100^\circ = 3.6

Since the number of monitors must be an integer, we round up.

Thus, at least 4 monitors are required.

Link Problem
Problem 5 Easy

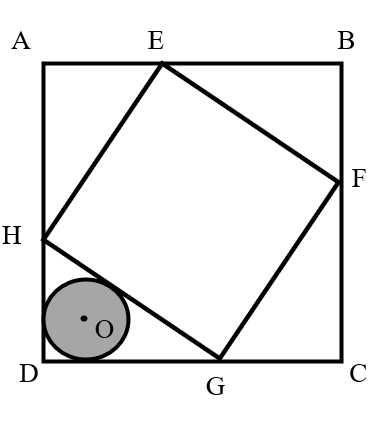
Given that the side length of square ABCD is 7 and the side length of square EFGH is 5, and square EFGH has an inscribed circle O, find the area of the circle.

  • A.

    \pi

  • B.

    4

  • C.

    \frac{3}{2}\pi

  • D.

    6

  • E.

    2\pi

Answer:A

It is known that the four right triangles are congruent.

The area of one such right triangle is: \frac{7^2 - 5^2}{4} = \frac{49 - 25}{4} = \frac{24}{4} = 6

Let the radius of circle O be r.

Since circle O is the inscribed circle (incircle) of the right triangle, connecting the three vertices of the triangle to the center O divides the triangle into three smaller triangles, each with a height equal to r.

\frac{1}{2} \times r \times HD + \frac{1}{2} \times r \times GD + \frac{1}{2} \times r \times FG = 6

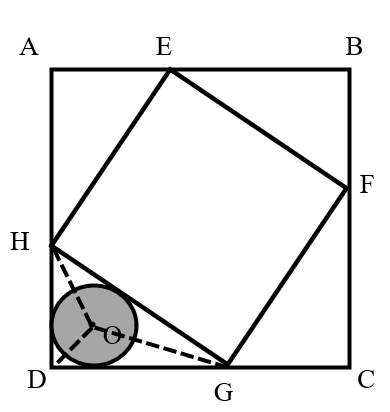
Factoring out \frac{1}{2}r, we get: \frac{1}{2}r \times (HD + GD + FG) = 6

Notice that HD + GD + FG is equal to the sum of the side length of the large square and the side length of the small square, 7 + 5 = 12.

Substituting this in:

\frac{1}{2}r \times 12 = 6

6r = 6

r = 1

Thus, the area of circle O is: \pi r^2 = \pi \times 1^2 = \pi

Answer: The area of the circle is \pi square units.

Link Problem
Problem 6 Easy

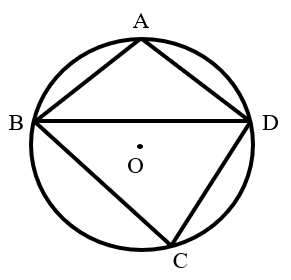
As shown in the figure, quadrilateral ABCD is inscribed in circle O, AB = CD, A is the midpoint of arc BD, and \angle BDC = 60^\circ. What is the measure of \angle ADB?

  • A.

    30

  • B.

    40^\circ

  • C.

    60^\circ

  • D.

    65^\circ

  • E.

    80^\circ

Answer:B

Connect AO, BO, CO, and DO.

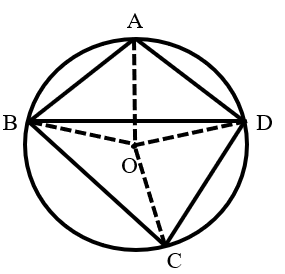
Since AB = CD, the arcs they subtend are equal, so arc AB = \text{arc } CD.

Because A is the midpoint of arc BD, arc AB = \text{arc } AD.

Therefore, arc AB = \text{arc } AD = \text{arc } CD.

\angle BDC is a circumferential angle subtended by arc BC, and \angle BDC = 60^\circ.

The central angle subtended by the same arc is twice the circumferential angle, so \angle BOC = 2 \times 60^\circ = 120^\circ.

The total degree measure of the circle is 360^\circ, so the sum of the central angles subtended by arcs AB, AD, and CD is: 360^\circ - \angle BOC = 360^\circ - 120^\circ = 240^\circ.

Since arc AB = \text{arc } AD = \text{arc } CD, their corresponding central angles are equal: \angle AOB = \angle AOD = \angle COD = \frac{240^\circ}{3} = 80^\circ.

\angle ADB is a circumferential angle subtended by arc AB , so it is half of the central angle \angle AOB: \angle ADB = \frac{1}{2} \times \angle AOB = \frac{1}{2} \times 80^\circ = 40^\circ.

Link Problem
Problem 7 Easy

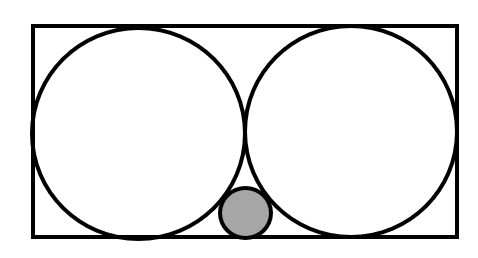
A rectangle is inscribed with two equal circles, each having an area of 16. A small circle is tangent to three figures (the two large circles and one side of the rectangle). What is the area of the small circle?

  • A.

    1

  • B.

    1

  • C.

    1

  • D.

    1

  • E.

    1

Answer:E

Let the radius of each large circle be R and the radius of the small circle be r.

Connecting the centers of the three circles forms a triangle.

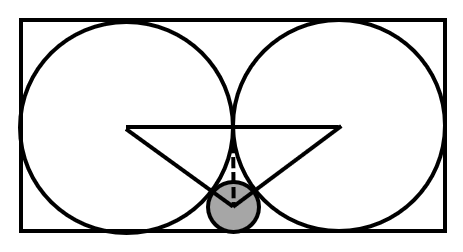
Based on the geometric relationship, we have the equation: R^2 + (R - r)^2 = (R + r)^2

Expanding and simplifying the equation:

R^2 + R^2 - 2Rr + r^2 = R^2 + 2Rr + r^2

2R^2 - 2Rr = R^2 + 2Rr

R^2 = 4Rr

R = 4r

The area of a large circle is given by: S_{\text{large circle}} = \pi R^2 = 16

Substituting R = 4r into the area formula of the large circle:

\pi (4r)^2 = 16, 16\pi r^2 = 16, \pi r^2 = 1

Thus, the area of the small circle is: S_{\text{small circle}} = \pi r^2 = 1.

Link Problem
Problem 8 Easy

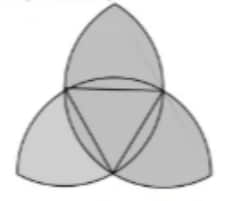
With each of the three vertices of an equilateral triangle with a side length of 2 centimeters as the center, arcs are drawn with a radius of 2 centimeters. What is the perimeter of the shaded figure in centimeters? (Take \pi = 3.14)

  • A.

    3.14

  • B.

    6.28

  • C.

    9.42

  • D.

    12.56

  • E.

    15.7

Answer:D

Each arc is \frac{1}{6} of the circumference of a circle because the central angle of each arc is 60^\circ.

Therefore, the perimeter of the shaded figure is composed of 6 such arcs.

The length of one arc is: \frac{1}{6} \times 2\pi r = \frac{1}{6} \times 2 \times 3.14 \times 2

The total perimeter of the shaded figure is: 6 \times \left( \frac{1}{6} \times 2 \times 3.14 \times 2 \right) = 2 \times 3.14 \times 2 = 12.56 \text{ centimeters}

Thus, the perimeter of the shaded figure is \boxed{12.56} centimeters.

Link Problem
Related Paper
AMC 8 Daily Practice Round 6 AMC 8 Daily Practice - Pythagorean Theorem AMC 8 Daily Practice - Solid Figures AMC 8 Daily Practice - Triangle Properties
Table of Contents
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
Think Academy Powered by ChatGPT