AMC 8 Daily Practice - Solid Figures
Complete problem set with solutions and individual problem pages
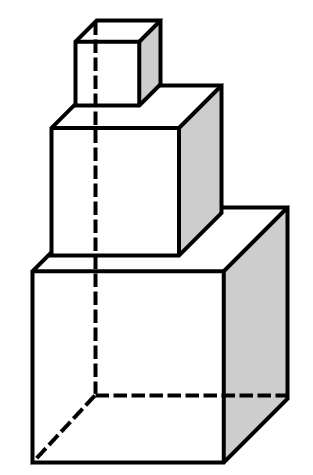
As shown in the figure below, three cubes with edge lengths of , , and are attached closely together. What is the surface area of the resulting three-dimensional figure in square centimeters?
- A.
- B.
- C.
- D.
- E.

Through observation, we find that when the three cubes are attached closely together, some surfaces are covered:
the bottom surface of cube , part of the top and bottom surfaces of cube , and part of the top surface of cube .
The total surface area is calculated as follows: .
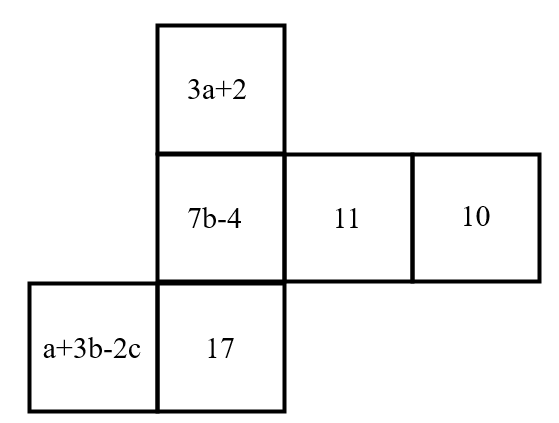
The following is a plane development diagram of a cube. If the values on the two opposite faces of the cube are equal, what is the value of ?
- A.
- B.
- C.
- D.
- E.
Through observation, we find three pairs of opposite faces as shown in the figure.
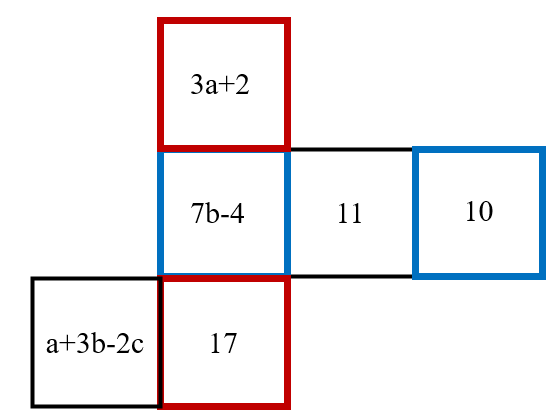
Since the values on opposite faces are equal, we have the following equations:
Solving these equations: -
From , we get , so .
From , we get , so . -
Substituting and into , we have , which simplifies to , so .
Finally, we calculate :
A square is cut off at one corner. Which of the following options could be its unfolded diagram?
- A.
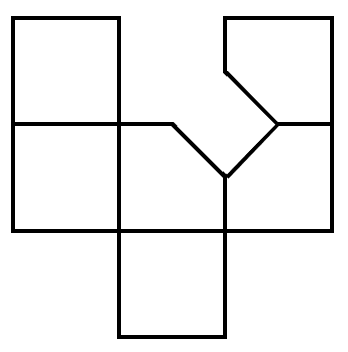
- B.
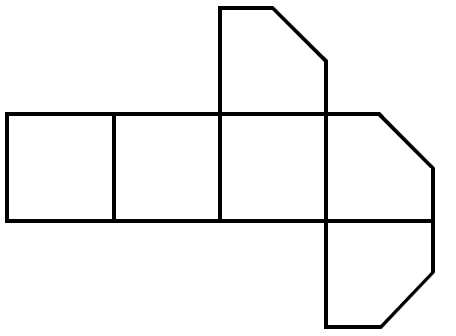
- C.
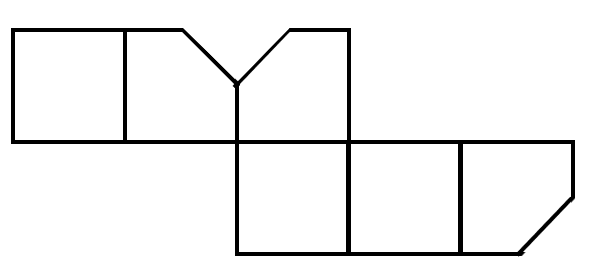
- D.
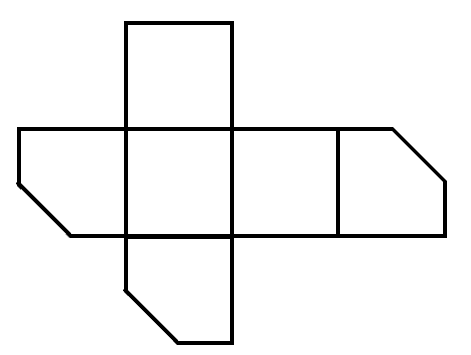
- E.
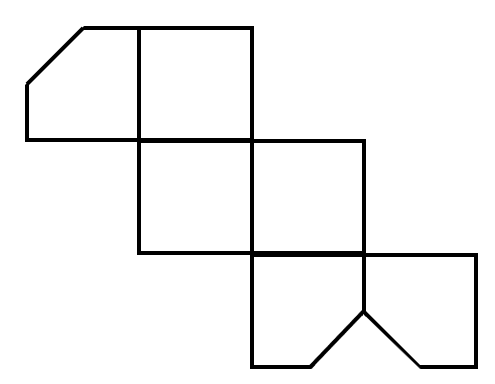
Assuming no corner is cut off, the corners of the square should converge at a single point.
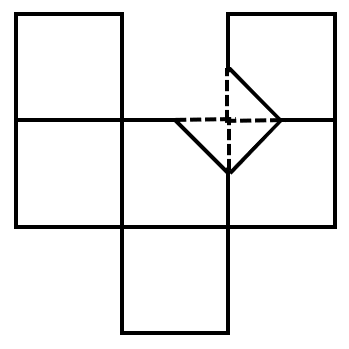
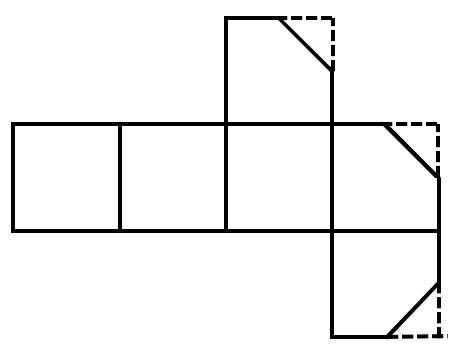
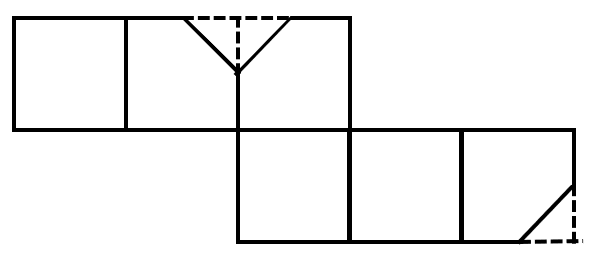
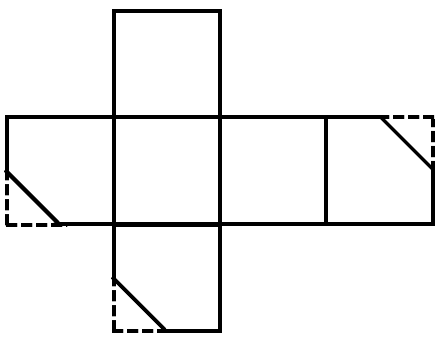
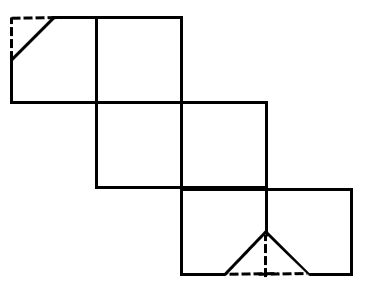
Options , , and do not converge at a single point, and is not a correct unfolded diagram. Therefore, the answer to this question is .
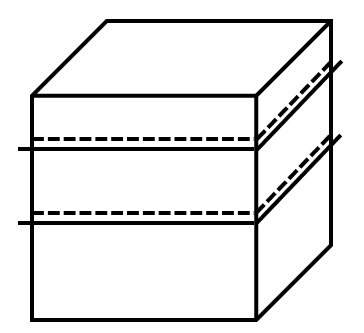
A cube is cut by two planes parallel to its base, dividing it into three rectangular prisms. The ratio of the surface areas of these three prisms is . What is the ratio of their volumes?
- A.
- B.
- C.
- D.
- E.
As shown in the figure, let the edge length of the cube be , and let the heights of the three rectangular prisms be , , and respectively.
Thus, we have: .
The surface area of each rectangular prism includes the two base areas (each equal to ) and the lateral surface area (equal to since the base is a unit square).
Therefore, the surface areas of the three prisms are , , and respectively.
Given their ratio is , we have: .
Solving this proportion, we find: .
Since the volumes of the prisms (with the same base area) are proportional to their heights, the ratio of their volumes is equal to the ratio of their heights: .
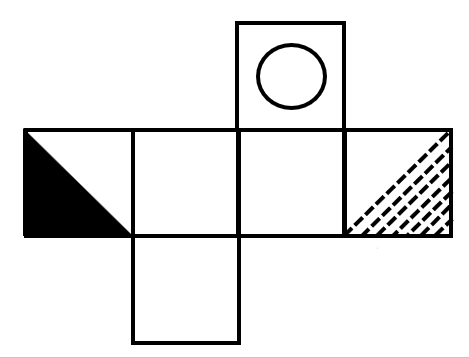
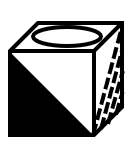
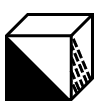
Mike folded a piece of paper into a cube-shaped box, put a gift inside, and mixed it with the boxes below. Which box contains the gift?
- A.
- B.

- C.

- D.
- E.

As shown in the figure, first identify the corresponding faces in the cube.

Based on the characteristics and positions of various symbols in the unfolded diagram, it is found that the black triangle and the slanted-line triangle should be adjacent faces with one side overlapping.
Therefore, the correct choice is .
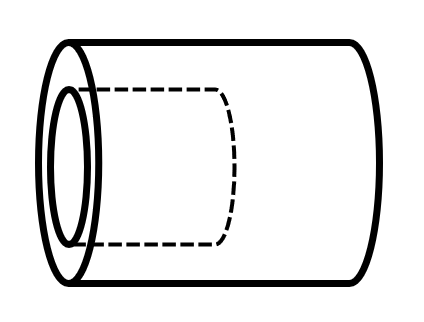
There is a cylindrical part with a height of centimeters and a base diameter of centimeters. One end of the part has a straight cylindrical hole, as shown in the figure: the diameter of the circular hole is centimeters, and the depth of the hole is centimeters. If the parts of this component that are exposed to air are to be painted with anti-rust paint, what is the total area to be painted in square centimeters?(For convenience, use .)
- A.
- B.
- C.
- D.
- E.
The total area to be painted includes the outer surface area of the cylinder, the inner surface area of the hole, and the area of the two circular bases (adjusted for the hole).
The calculation is as follows:
The total area to be painted is square centimeters.
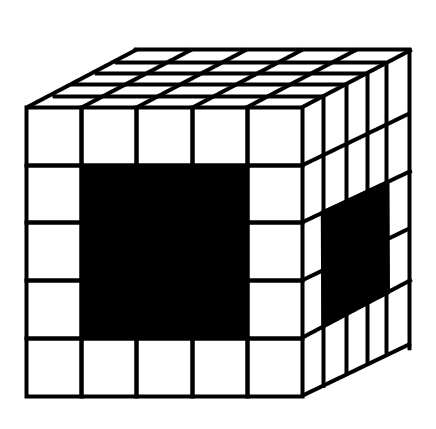
There is a cube wooden block with an edge length of . There are penetrating holes (shown as black parts in the figure) when viewed from the front and the right side. What is the volume of this three-dimensional figure in cubic centimeters?
- A.
- B.
- C.
- D.
- E.
We can calculate the volume by dividing the cube into five layers from top to bottom:

The first and fifth layers have no holes, and the volume of each layer is cubic centimeters.
The volume of the second layer is cubic centimeters.
The volume of the third layer is cubic centimeters.
The volume of the fourth layer is cubic centimeters.
Adding them up, the total volume is: cubic centimeters.
There is a sufficiently deep water tank with a rectangular base of length and width . Originally, the tank contains water with a depth of and oil (above the water) with a depth of . An iron block with length , width , and height is placed into the tank. What is the height of the oil layer at this time, in centimeters?
- A.
- B.
- C.
- D.
- E.
After placing the iron block, the base area of the water layer becomes: .
The height of the water layer changes to: .
This indicates that a -centimeter height of the iron block is submerged in water, and a -centimeter height of the iron block is immersed in oil.
The volume of the oil layer increases by: .
The increased height of the oil layer is: .
Thus, the height of the oil layer at this time is: .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
