AMC 8 Daily Practice - Triangle Properties
Complete problem set with solutions and individual problem pages
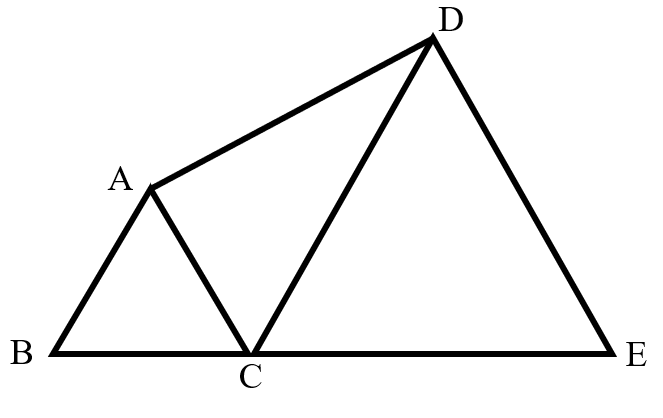
As shown in the figure, , , and . What is the value of ?
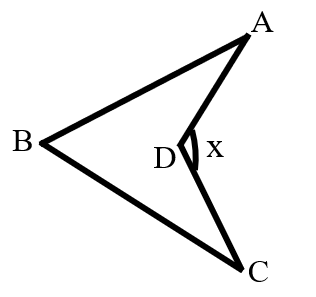
- A.
- B.
- C.
- D.
- E.
Connect .
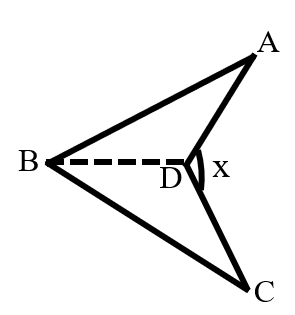
In , .
In , .
Then,
Thus, .
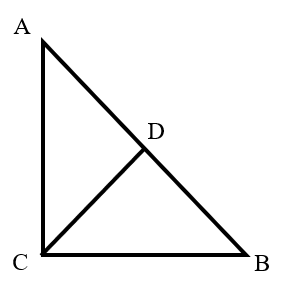
As shown in the figure, in triangle , , , point is the midpoint of side , and bisects the perimeter of triangle . What is the length of ?
- A.
- B.
- C.
- D.
- E.
Since bisects the perimeter of triangle , the perimeter of triangle is equal to the perimeter of triangle .
That is: .
Simplifying, we get: .
Since is the midpoint of , .
Substituting this into the equation above, we have:
Given , it follows that .
In the right triangle with , by the Pythagorean theorem: .
Since is the midpoint of , the length of is: .
In a triangle, the largest angle is times the smallest angle, and the other angle is times the smallest angle. What is the degree measure of the largest angle?
- A.
- B.
- C.
- D.
- E.
Let the three angles of the triangle be , , and , where .
According to the problem, we know that and .
Thus, the ratio of the angles is .
Since the sum of the interior angles of a triangle is , the measure of the largest angle is: .
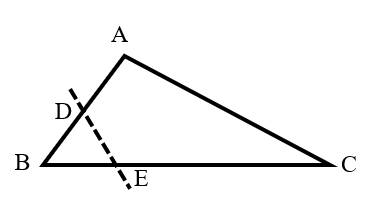
In triangle , . If is cut off along the dashed line, what is the sum of and ?
- A.
- B.
- C.
- D.
- E.
We know that: , .
Then, the sum of and is: .
In , .
Substituting this in, we get:
Since : .
Two equilateral triangles and lie on the same horizontal plane, with areas and respectively. What is the area of triangle ?
- A.
- B.
- C.
- D.
- E.
Since triangles and are equilateral, and .
Given that the area of a triangle is , we have:
: = :
: = :
Since and , it follows that: .
Let the area of be .
Then: .
Solving for : .
Thus, the area of is .
The perimeter of a triangle is , and its shortest side is . If all three sides of the triangle are integers, what is the maximum possible length of the longest side in centimeters?
- A.
- B.
- C.
- D.
- E.
Assume the three sides of the triangle, arranged in ascending order, are , , and .
According to the triangle inequality theorem, the sum of any two sides of a triangle must be greater than the third side, so: .
Since the perimeter of the triangle is cm, we have: , which simplifies to: .
Substituting into the inequality , we get: , , , .
Since is an integer, the maximum possible value of is .
Thus, the longest side can be at most centimeters.
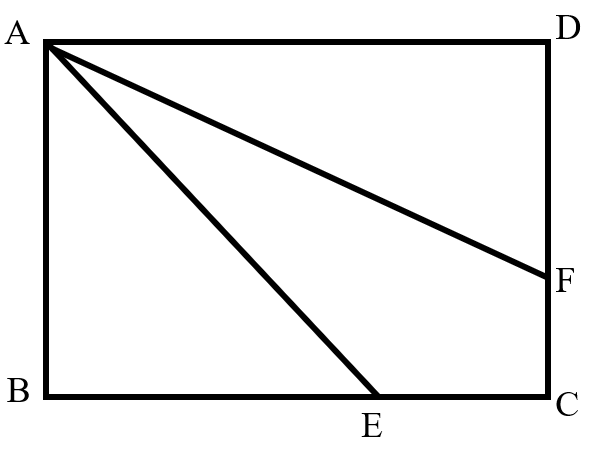
In rectangle , and . The two line segments and divide the area of the rectangle into three equal parts. What is the area of triangle ?
- A.
- B.
- C.
- D.
- E.
The area of rectangle is .
The area of is , so .
The area of is , so .
Connect .

The area of is .
Therefore, the area of is:
Substituting the values and : .
Thus, the area of is .
What is the largest whole number smaller than the perimeter of any triangle with a side of length and a side of length ?
- A.
- B.
- C.
- D.
- E.
From the Triangle Inequality Theorem, we know that for the third side of the triangle, the following must hold: and .
Let be the perimeter of the triangle, so .
Adding to all parts of the inequality for , we get:
Thus, the largest whole number smaller than the perimeter of any such triangle is .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
