AMC 8 Daily Practice - Area Tricks
Complete problem set with solutions and individual problem pages
The area of quadrilateral is . It is known that , , and . What is the area of the shaded part?

- A.
- B.
- C.
- D.
- E.
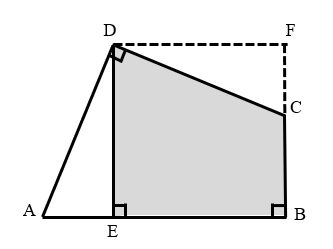
Since , as shown in the figure, draw a line through point perpendicular to the extension of at point .
It can be obtained that (congruent triangles).
Therefore, quadrilateral can be transformed into square .
The area of square is , so .
Then, .
Thus, the area of the shaded part is:
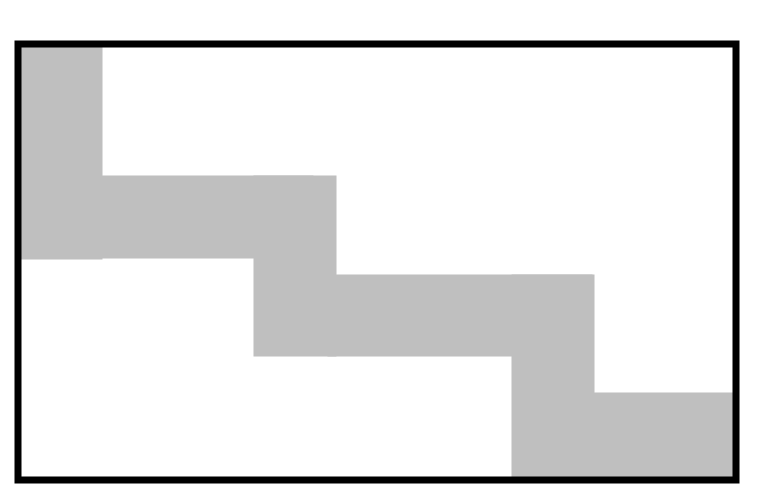
There is a rectangular flower bed. In the middle of the flower bed, there is a pedestrian path with a width of meters. The flower bed is meters long and meters wide. What is the area of the pedestrian path in square meters?
- A.
- B.
- C.
- D.
- E.
Through observation, we can translate the path to the position as shown in the following figure.

Therefore, the area of the pedestrian path is calculated as:
As shown in the figure below, the side length of square is centimeters, and the rectangle has a length of centimeters and a width of centimeters. What is the difference between the areas of the two shaded parts?
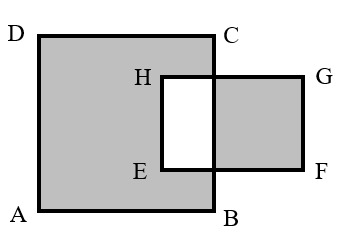
- A.
- B.
- C.
- D.
- E.
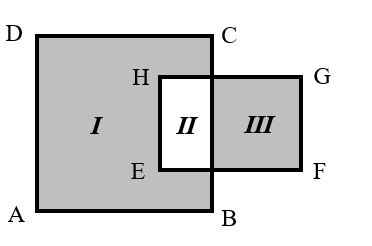
As shown in the figure, let the areas of the three regions be denoted as , , and respectively.
We have:
Then, the difference between the areas of the two shaded parts is:
Rectangle has a length of centimeters and a width of centimeters. Its diagonals and divide it into four parts, and diagonal is further divided into four equal segments. What is the area of the shaded part?
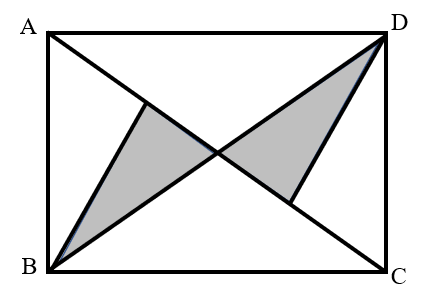
- A.
- B.
- C.
- D.
- E.

According to the formula for the area of a triangle: .
The area of triangle = the area of triangle = the area of triangle = the area of triangle .
The area of the shaded part is calculated as:
Square has a side length of centimeters. It is known that , centimeters, and centimeters. What is the area of the shaded part?
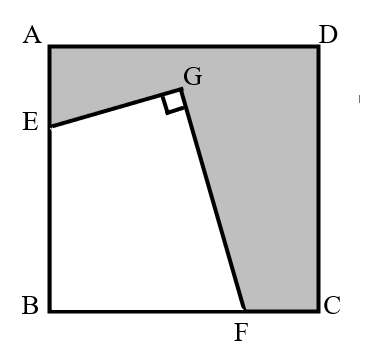
- A.
- B.
- C.
- D.
- E.
Since , we can fold the figure as shown, resulting in a new figure.

Through this folding, the area of the shaded part can be calculated as follows: .
Thus, the area of the shaded part is square centimeters.
The area of a regular octagon is square centimeters. What fraction of the area of the octagon is shaded?
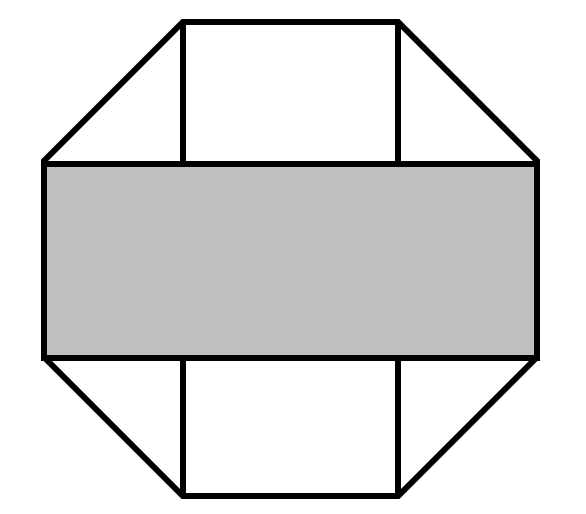
- A.
- B.
- C.
- D.
- E.
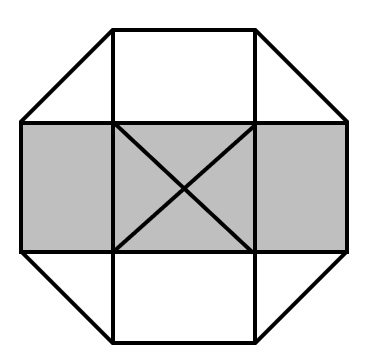
By means of division, the octagon is divided into rectangles and triangles.
The shaded part contains rectangles and triangles.
Therefore, the area of the shaded part accounts for of the total area.
A large square and a small square are placed side by side, with the side length of the small square being . What is the area of the shaded part?
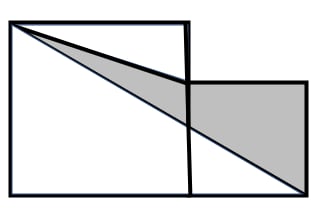
- A.
- B.
- C.
- D.
- E.
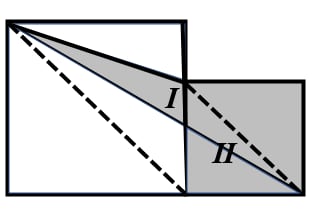
As shown in the figure, connect the diagonals of the two squares.
Since the two diagonals are parallel, we find that the area of triangle is equal to the area of triangle .
Therefore, the area of the shaded part is converted to the area of the small square, which is:
In rectangle , and are the midpoints of and respectively. Given that and , what is the area of the rectangle?
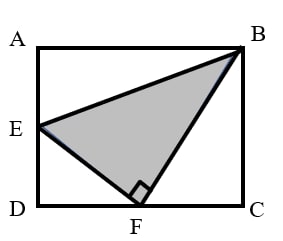
- A.
- B.
- C.
- D.
- E.
Draw through point parallel to , and draw through point parallel to .
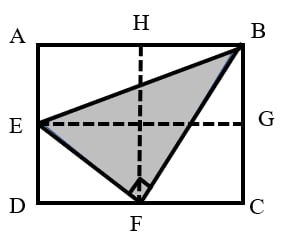
We observe that:
The area of is of the area of the rectangle.
The area of is of the area of the rectangle.
The area of is of the area of the rectangle.
Therefore, the area of is of the area of the rectangle.
The area of is calculated as: .
Let the area of the rectangle be .
Then: .
Solving for : .
Thus, the area of the rectangle is .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
