AMC 8 Daily Practice - Multiplication Formula

Complete problem set with solutions and individual problem pages

Problem 1 Easy

What is the value of 9999^2 + 19999？

  • A.

    100000000

  • B.

    19999998

  • C.

    9999

  • D.

    199999999

  • E.

    99999999

Answer:A

9999^2 + 19999 = 9999^2 + 9999 \times 2 + 1= 9999^2 + 2 \times 9999 \times 1 + 1^2= (9999 + 1)^2 = 10000^2= 100000000

Final result:  \boxed{100000000}

Link Problem
Problem 2 Easy

Given a real number x satisfies the equation:   (x - 2023)^2 + (2024 - x)^2 = 2025, what is the value of (x - 2023)(2024 - x)?

  • A.

    -1013

  • B.

    -1012

  • C.

    1012

  • D.

    1013

  • E.

    2025

Answer:B

Let a = x - 2023.

Then, we can express 2024 - x as:   2024 - x =1 - a

Substituting these into the original equation:

a^2 + (1 - a)^2 = 2025

a^2 + \left(1 - 2a + a^2\right) = 2025

2a^2 - 2a + 1 = 2025

2a^2 - 2a - 2024 = 0

a^2 - a = 1012

Observe that: (x - 2023)(2024 - x)=a(1-a)= a - a^2

From the simplified quadratic equation a^2 - a = 1012, multiply both sides by -1:   -a^2 + a = -1012.

Thus, the value of (x - 2023)(2024 - x) is:   -1012

Final result: \boxed{-1012 }

Link Problem
Problem 3 Easy

What is the value of \frac{10^{2}-9^{2}+8^{2}-7^{2}+6^{2}-5^{2}+4^{2}-3^{2}+2^{2}-1^{2}}{10+9+8+7+6+5+4+3+2+1}？

  • A.

    10

  • B.

    5

  • C.

    3

  • D.

    2

  • E.

    1

Answer:E

\frac{10^{2} - 9^{2} + 8^{2} - 7^{2} + 6^{2} - 5^{2} + 4^{2} - 3^{2} + 2^{2} - 1^{2}}{10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1}

=\frac{(10 - 9)(10 + 9) +(8 - 7)(8 + 7) + (6 - 5)(6 + 5) + (4 - 3)(4 + 3) + (2 - 1)(2 + 1)}{10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1}

=\frac{(10 + 9) +(8 + 7) + (6 + 5) + (4 + 3) + (2 + 1)}{10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1}

=1

Final Answer: \boxed{1}

Link Problem
Problem 4 Easy

If A = (2+1)(2^2+1)(2^4+1)\cdots(2^{32}+1)+1, what is the units digit of A?

  • A.

    0

  • B.

    2

  • C.

    4

  • D.

    6

  • E.

    8

Answer:D

A = (2+1)(2^2+1)(2^4+1)\dots(2^{32}+1)+1\\

=(2-1)(2+1)(2^2+1)(2^4+1)\dots(2^{32}+1)+1 \\

=(2^2-1)(2^2+1)(2^4+1)\dots(2^{32}+1)+1 \\

=(2^4-1)(2^4+1)\dots(2^{32}+1)+1 \\

=(2^{32}-1)(2^{32}+1)+1 \\

= 2^{64}-1+1 \\

= 2^{64}

Since 2^n cycles every 4: 2^1=2, 2^2=4, 2^3=8, 2^4=6, \dots

64 \div 4 = 16 remainder 0, so 2^{64} has units digit 6.

Final result: The units digit of A is \boxed{6}.

Link Problem
Problem 5 Easy

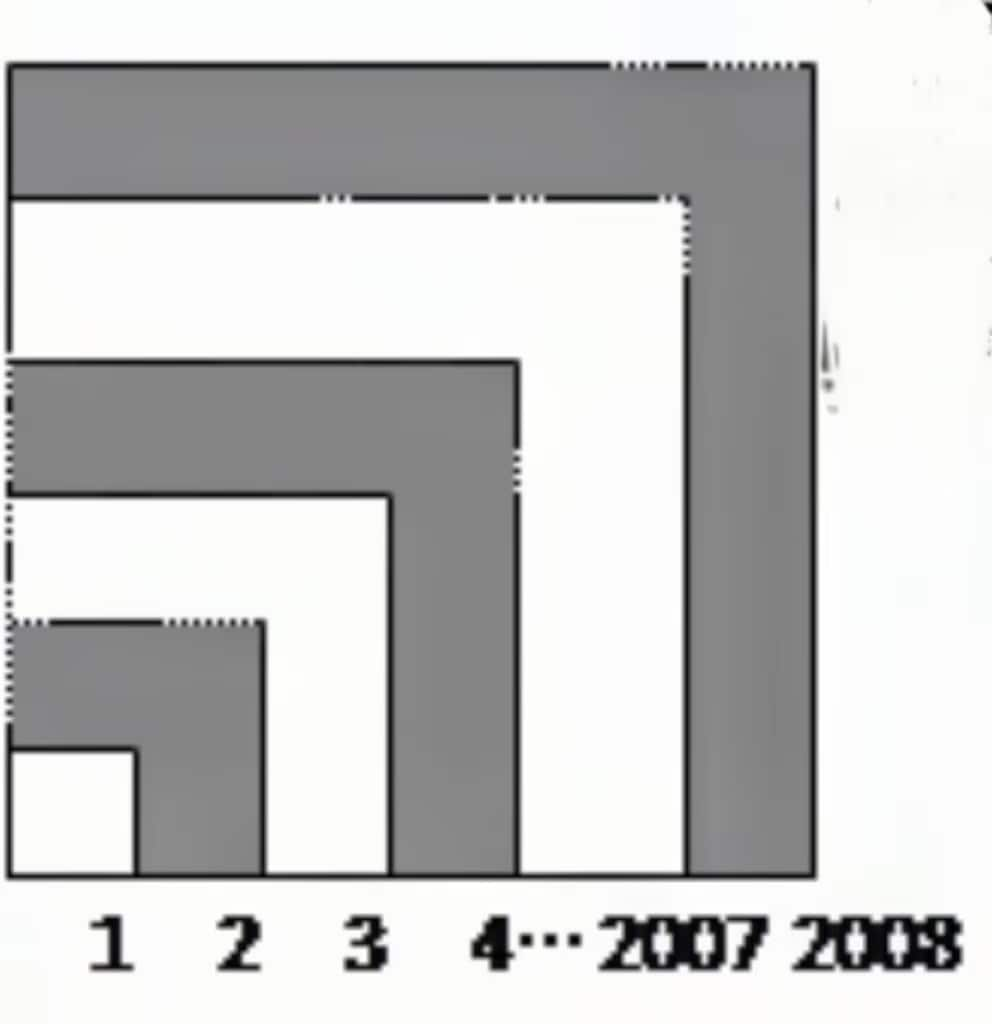
Calculate the shaded area formed by overlapping squares with side lengths 1, 2, 3, \ldots, 2008.

  • A.

    2008000

  • B.

    2009000

  • C.

    2017036

  • D.

    1000000

  • E.

    2007000

Answer:C

The shaded area is the alternating sum of squares:

(2^2-1^2) + (4^2-3^2) + \cdots + (2008^2-2007^2) \\

= (2+1)(2-1) + (4+3)(4-3) + \cdots + (2008+2007)(2008-2007) \\

= 1 + 2 + 3 + \cdots + 2008 \\

= \frac{2008 \times (1+2008)}{2} = 2017036

Final result: \boxed{2017036}

Link Problem
Problem 6 Easy

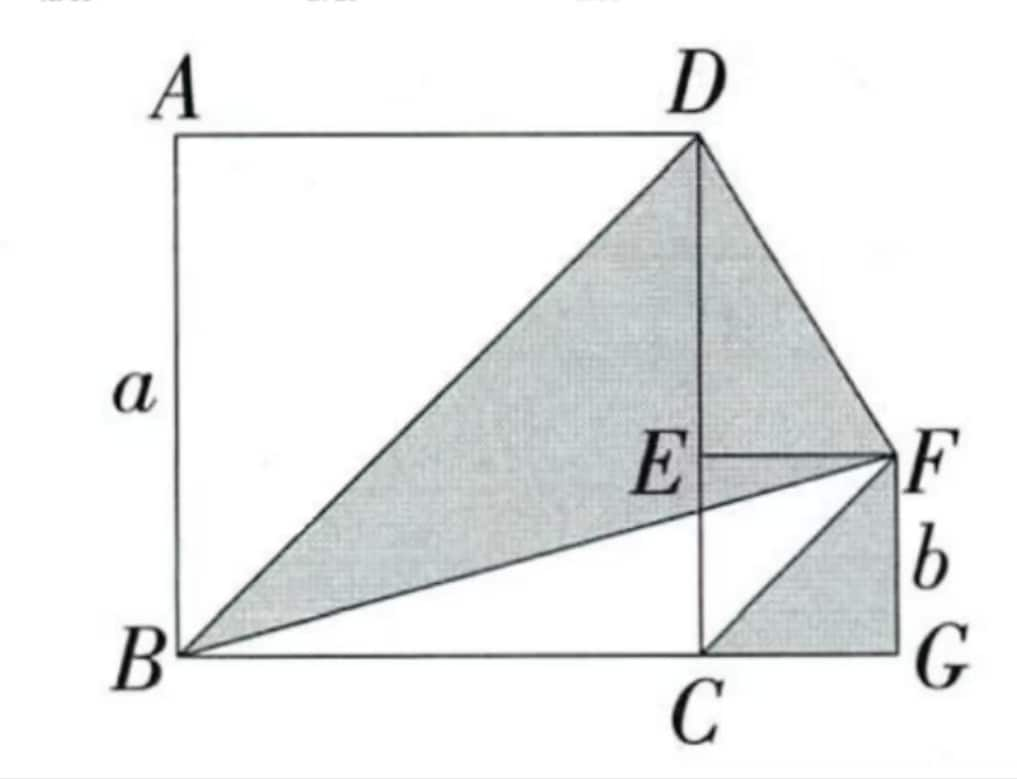
Two squares with sides a and b satisfy a+b=10 and ab=20.Find the shaded area.

  • A.

    20

  • B.

    30

  • C.

    40

  • D.

    45

  • E.

    60

Answer:B

Shaded area

A = \frac{1}{2}a^2 + \frac{1}{2}b(a+b) - \frac{1}{2}ab = \frac{1}{2}(a^2 + b^2).

From (a+b)^2 = a^2 + 2ab + b^2 = 100 \implies a^2 + b^2 = 100 - 40 = 60

Therefore A = \frac{1}{2} \times 60 = 30

Final result: \boxed{30}

Link Problem
Problem 7 Easy

The number 2^{48}-1 is divisible by two integers between 60 and 70. What are these integers?

  • A.

    63,65

  • B.

    63,64

  • C.

    64,65

  • D.

    65,66

  • E.

    67,68

Answer:A

2^{48}-1 = (2^{24}-1)(2^{24}+1) \\

= (2^{12}-1)(2^{12}+1)(2^{24}+1) \\

= (2^6-1)(2^6+1)(2^{12}+1)(2^{24}+1) \\

= 63 \times 65 \times (2^{12}+1)(2^{24}+1)

The factors between 60-70 are 63 and 65.

Final results: \boxed{63,65}

Link Problem
Problem 8 Medium

A four-digit perfect square has all its digits less than 7. When 3 is added to each of its digits, the resulting number is also a perfect square. What is the original four-digit number?

  • A.

    1089

  • B.

    1156

  • C.

    1225

  • D.

    1296

  • E.

    1369

Answer:B

Let the number be \overline{abcd} = m^2.

After adding 3 to each digit: \overline{(a+3)(b+3)(c+3)(d+3)} = n^2.

n^2 - m^2 = 3333 = (n-m)(n+m).

Factor pairs of 3333: 1 \times 3333, 3 \times 1111, 11 \times 303, 33 \times 101. Only 33 \times 101 satisfies.

n+m=101 and n-m=33 \implies m=34.

Original number: 34^2 = 1156.

Final result: \boxed{1156}

Link Problem
Related Paper
AMC 8 Daily Practice - Area Tricks AMC 8 Daily Practice - Perimeter Tricks AMC 8 Daily Practice - The Sum of a Finite Arithmetic Series AMC 8 Daily Practice - The Rule of Arithmetic Sequences
Table of Contents
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
Think Academy Powered by ChatGPT