AMC 8 Daily Practice - Multiplication Formula
Complete problem set with solutions and individual problem pages
Given a real number satisfies the equation: , what is the value of ?
- A.
- B.
- C.
- D.
- E.
Let .
Then, we can express as:
Substituting these into the original equation:
Observe that:
From the simplified quadratic equation , multiply both sides by : .
Thus, the value of is:
Final result:
If , what is the units digit of ?
- A.
- B.
- C.
- D.
- E.
Since cycles every :
remainder 0, so has units digit .
Final result: The units digit of is .
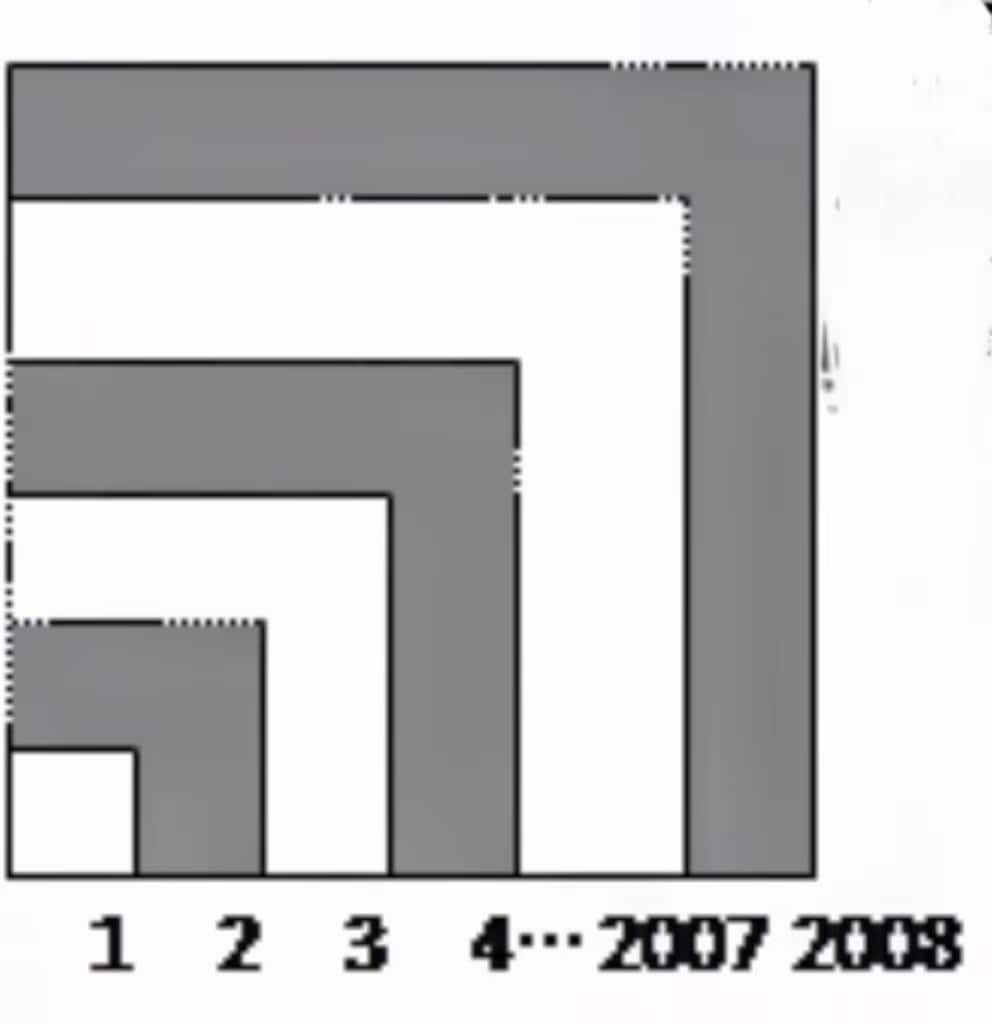
Calculate the shaded area formed by overlapping squares with side lengths .
- A.
- B.
- C.
- D.
- E.
The shaded area is the alternating sum of squares:
Final result:
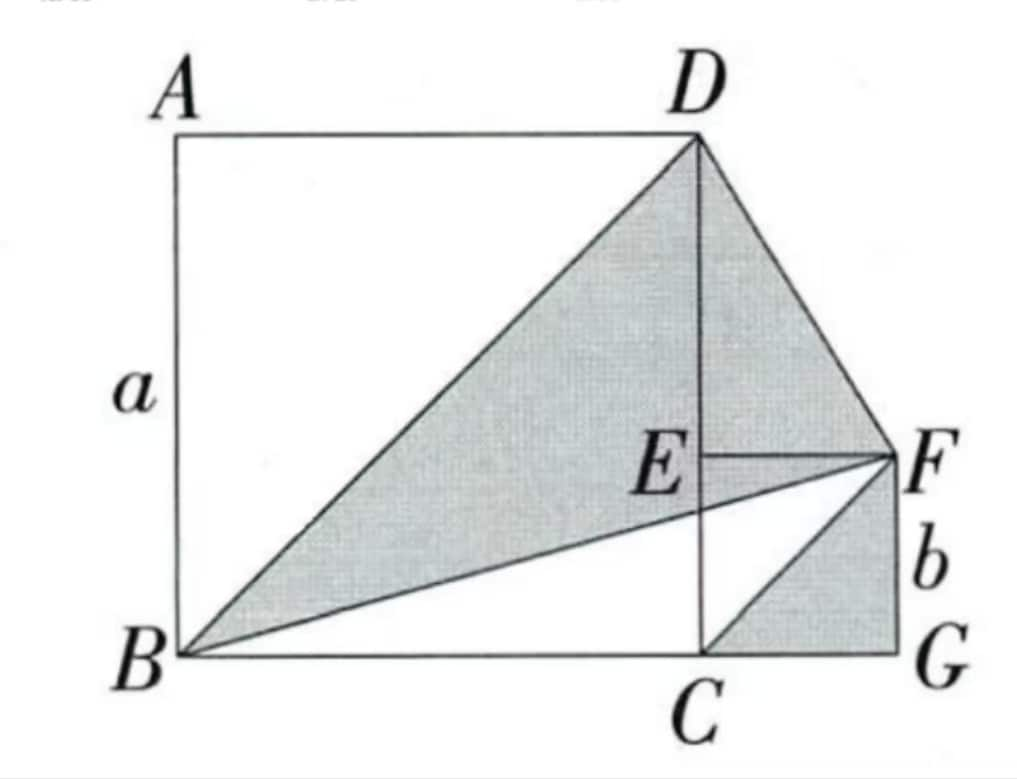
Two squares with sides and satisfy and .Find the shaded area.
- A.
- B.
- C.
- D.
- E.
Shaded area
.
From
Therefore
Final result:
The number is divisible by two integers between and . What are these integers?
- A.
- B.
- C.
- D.
- E.
The factors between are and .
Final results:
A four-digit perfect square has all its digits less than . When is added to each of its digits, the resulting number is also a perfect square. What is the original four-digit number?
- A.
- B.
- C.
- D.
- E.
Let the number be .
After adding to each digit: .
.
Factor pairs of : . Only satisfies.
and .
Original number: .
Final result:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
