AMC 8 Daily Practice - The Sum of a Finite Arithmetic Series
Complete problem set with solutions and individual problem pages
A town hall clock chimes the hour number on every full hour and once on every half-hour. How many chimes will occur in a full -hour period?
- A.
- B.
- C.
- D.
- E.
Daily chimes:
Four campers—Alice, Bob, Charlie, and Diana—play a number-reporting game around a campfire. In Round , Alice reports , Bob reports and , Charlie reports , , , and Diana reports , , , . In Round , Alice continues with through , maintaining the same pattern. How many numbers did Alice report in the first five rounds?
- A.
- B.
- C.
- D.
- E.
Alice's reporting pattern follows an arithmetic sequence where the number of terms per round increases by each time: terms for Rounds to .
Using the arithmetic series sum formula:
Final result:
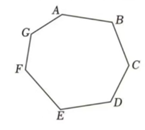
A game piece starts at vertex of a heptagon board labeled clockwise. Players move the piece times following this rule: on the -th move, jump vertices clockwise. Which vertices remain unvisited after moves?
- A.
- B.
- C.
- D.
- E.
Label the vertices as (A), (B), (C), (D), (E), (F), and (G).
After moves, the total number of positions traversed is:
The final position is determined by computing the remainder when is divided by :
By calculating for , we observe the repeating sequence of remainders: .
Vertices corresponding to remainders , , and (i.e., C, E, and F) are never visited.
Final result:
A retirement community has residents with integer ages summing to . The oldest resident is aged but , while the remaining residents have consecutive ages. What is the age range of the community?
- A.
- B.
- C.
- D.
- E.
Let minimum age be . The sequence is:
Sum equation:
Given , solve:
Thus , and age range .
Final result:
Given the sequence , what is the term of this sequence?
- A.
- B.
- C.
- D.
- E.
This sequence represents triangular numbers with the -th term formula:
For :
Final result:
An arithmetic sequence has its term as and term as . How many of the first terms are integers?
- A.
- B.
- C.
- D.
- E.
Common difference .
Integer terms occur when .
In terms:
Final result:
students line up to count consecutively starting at , with each subsequent number increasing by . One student wistakenly subtracts instead, resulting in a total sum of . Which student made the counting error?
- A.
- B.
- C.
- D.
- E.
If all students counted correctly, the sequence forms an arithmetic progression with: First term , Common difference , term: .
The correct sequence would be . The total sum is:
The discrepancy between the correct sum and actual sum is:
Starting from the erroneous student, each subsequent student's number is less than expected.
The number of affected terms is:
Thus, the error occurs at position:
Final result:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
