AMC 8 Daily Practice - The Rule of Arithmetic Sequences

Complete problem set with solutions and individual problem pages

Problem 1 Easy

Halley's Comet has been observed passing by Earth in the years 1682, 1758, 1834, 1910, and 1986. Based on the pattern, when might it return in this century?

  • A.

    2000

  • B.

    2025

  • C.

    2037

  • D.

    2062

  • E.

    2076

Answer:D

Observing the years forms an arithmetic sequence with the first term 1682 and a common difference 76.

The next return year would be: 1986 + 76 = 2062

Final result: \boxed{2062}

Link Problem
Problem 2 Easy

John plans to train for a 5000m race with a 15-day program: 5000m on Day 1, increasing by 300m daily. How far will he run on Day 15?

  • A.

    4700m

  • B.

    7400m

  • C.

    8000m

  • D.

    9200m

  • E.

    9500m

Answer:D

This forms an arithmetic sequence with a_1 = 5000 and d = 300.

Using the nth-term formula: a_{15} = 5000 + 300 \times (15-1) = 5000 + 4200 = 9200m

Final result: \boxed{9200} meters

Link Problem
Problem 3 Easy

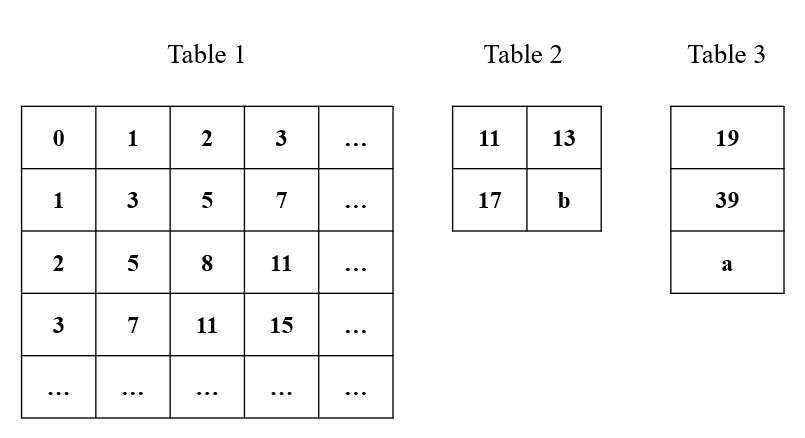
Table 2 and Table 3 are part of Table 1. What is the value of a+b?

  • A.

    37

  • B.

    40

  • C.

    49

  • D.

    59

  • E.

    79

Answer:E

From Table 1's column pattern: a - 39 = 39 - 19 \implies a = 59.

From Table 1's row pattern: b - 13 = 17 - 11 + 1 \implies b = 20.

Thus: a + b = 59 + 20 = 79.

Final result: \boxed{79}

Link Problem
Problem 4 Easy

A 5-shelf bookcase holds 450 books. Each upper shelf has 10 fewer books than the one below. How many books on the top shelf?

  • A.

    10

  • B.

    70

  • C.

    90

  • D.

    200

  • E.

    450

Answer:B

Let shelves be 1 (top) to 5.

The middle shelf (3rd) has: 450\div5 = 90 books.

Top shelf: 90 - 10 - 10 = 70.

 Final result: \boxed{70} books

Link Problem
Problem 5 Easy

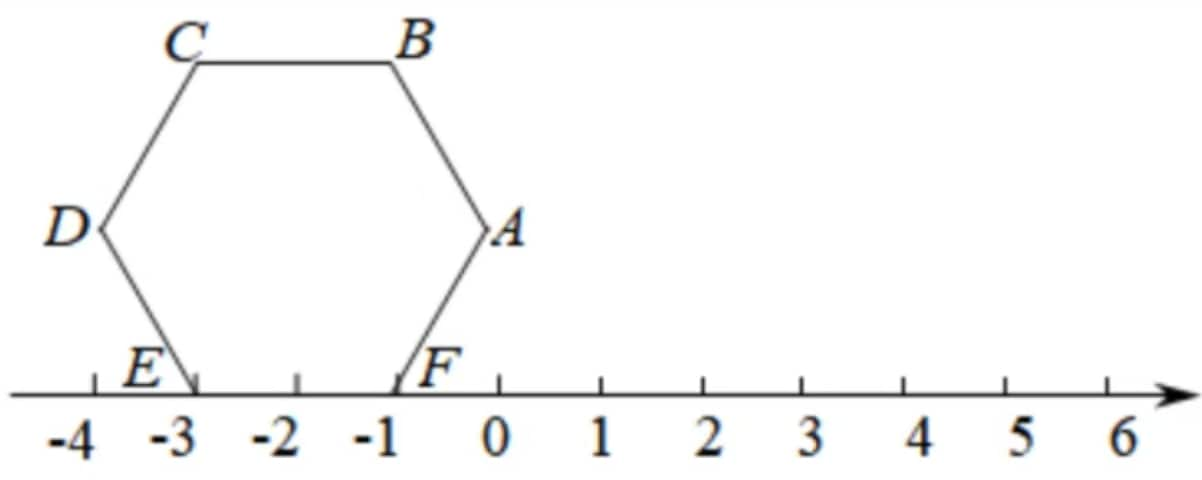
As shown in the diagram, a regular hexagon ABCDEF (with all sides equal) is positioned on a number line. Points E and F correspond to numbers-3 and -1, respectively. When the hexagon is rotated clockwise around a vertex, after 1 rotation, point A aligns with the number 1. Continuing this rotation pattern, identify which vertex of the hexagon corresponds to the number 4041 on the number line.

  • A.

    E

  • B.

    D

  • C.

    C

  • D.

    B

  • E.

    A

Answer:A

From the first rotation, point A moves to 1, indicating the side length of the hexagon is 2 (distance between -1 and 1).

Observing the rotation pattern:

- After 1 rotation: Point A → 1

- After 2 rotations: Point B → 3

- After 3 rotations: Point C → 5

- After 4 rotations: Point D → 7

- After 5 rotations: Point E → 9

- After 6 rotations: Point F → 11

- After 7 rotations: Point A → 13

This establishes a periodic pattern with period 6.

The general formula for the position after n rotations is:

\text{Position} = -1 + 2n

Set -1 + 2n = 4041\Rightarrow \quad2n = 4042 \quad \Rightarrow \quad n = 2021

Determine the position within the 6-rotation cycle:   2021 \div 6 = 336 \text{ remainder } 5

A remainder of 5 corresponds to the 5th vertex in the cycle (E).

Final result: \boxed{E}

Link Problem
Problem 6 Easy

Given that both sequences a_1, a_2, \ldots, a_{31} and b_1, b_2, \ldots, b_{31} are arithmetic sequences, each containing 31 terms. If a_2 + b_{30} = 29 and a_{30} + b_2 = -9, find the total sum of these two sequences.

  • A.

    29

  • B.

    60

  • C.

    200

  • D.

    310

  • E.

    400

Answer:D

For arithmetic sequences, the sum of terms equidistant from the ends is constant: a_1 + a_{31} = a_2 + a_{30}, \quad b_1 + b_{31} = b_2 + b_{30}.

By pairing terms symmetrically: (a_1 + b_{31}) + (b_1 + a_{31}) = (a_2 + b_{30}) + (b_2 + a_{30}) = 29 + (-9) = 20.

There are 15 such pairs.

Including the middle terms (which also sum to 10), the total sum is: 15 \times 20 + 10 = 310.

Final result: \boxed{310}

Link Problem
Problem 7 Easy

Lily wants to distribute 210 chess pieces into several boxes. The first box contains 1 piece, the second box contains 2 pieces, the third box contains 3 pieces, and so on. The pieces are exactly when placed in this manner. How many boxes does Lily use?

  • A.

    18

  • B.

    19

  • C.

    20

  • D.

    21

  • E.

    22

Answer:C

Assume Lily uses n boxes.

The total number of pieces follows the arithmetic series:   1 + 2 + 3 + \dots + n = 210

Using the arithmetic series sum formula:   \frac{n(n+1)}{2} = 210

Multiply both sides by 2:   n(n+1) = 420

Solve the quadratic equation:   n^2 + n - 420 = 0

Factorizing:   (n - 20)(n + 21) = 0

Since n > 0, we get n = 20.

Final result: \boxed{20}

Link Problem
Problem 8 Easy

How many integers between 401 and 1000 (inclusive) leave a remainder of 1 when divided by 8?

  • A.

    72

  • B.

    73

  • C.

    74

  • D.

    75

  • E.

    76

Answer:D

These integers form an arithmetic sequence with first term 1, common difference 8, and general term 8n-7.

Within the range 401–1000:

The smallest term is 401 (when n=51: 8 \times 51 - 7 = 401).

The largest term is 993 (when n=125: 8 \times 125 - 7 = 993).

The number of terms is calculated as: \frac{993 - 401}{8} + 1 = \frac{592}{8} + 1 = 74 + 1 = 75

Final result: \boxed{75}

Link Problem
Related Paper
AMC 8 Daily Practice - Multiplication Formula AMC 8 Daily Practice - The Sum of a Finite Arithmetic Series AMC 8 Daily Practice - New Patterns AMC 8 Daily Practice - Consecutive Reduction
Table of Contents
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
Think Academy Powered by ChatGPT