AMC 8 Daily Practice Round 3
Complete problem set with solutions and individual problem pages
Lucy wants to make a drink, which is made by sugar, salt, and water. The sugar concentration of the drink should be %, and the salt concentration should be %. She adds grams of sugar and some grams of salt to the cup. How many grams of water does Lucy need?
- A.
- B.
- C.
- D.
- E.
% =
% =
How many four-digit numbers are divisible by ?
- A.
- B.
- C.
- D.
- E.
Let be any positive integer so that is a multiple of . For the smallest four-digit number, and . For the greatest four-digit number, and . The number can be in the range to . Thus, there are numbers in total.
In the grid below, the distance between each two neighboring points is . What is the area of the shaded quadrilateral?

- A.
- B.
- C.
- D.
- E.
The side length of a triangle are three consecutive integers. The length of the longest side is of the perimeter of the triangle. What is the length of the longest side?
- A.
- B.
- C.
- D.
- E.
Let , , and be the lengths of the sides of the triangle. Then the perimeter of the triangle is . Using the fact that the length of the longest side is of the perimeter, it follows that: . The longest side is . Thus, answer is correct.
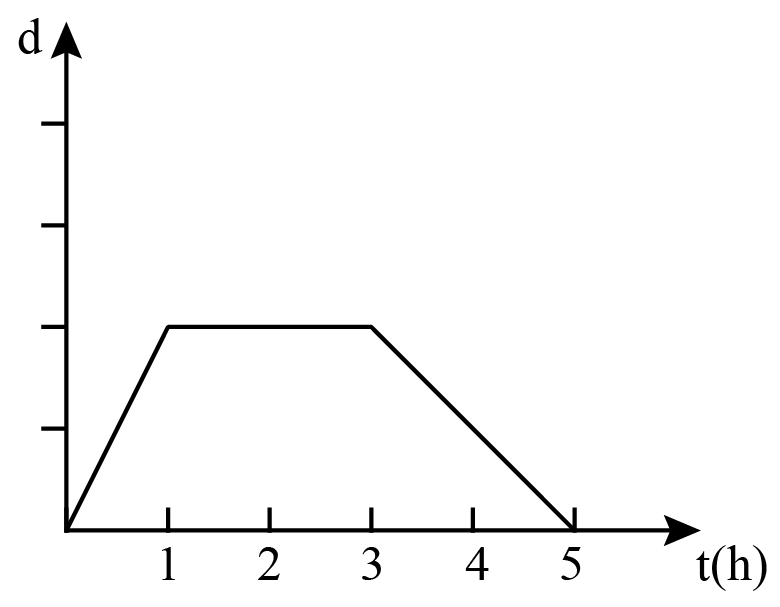
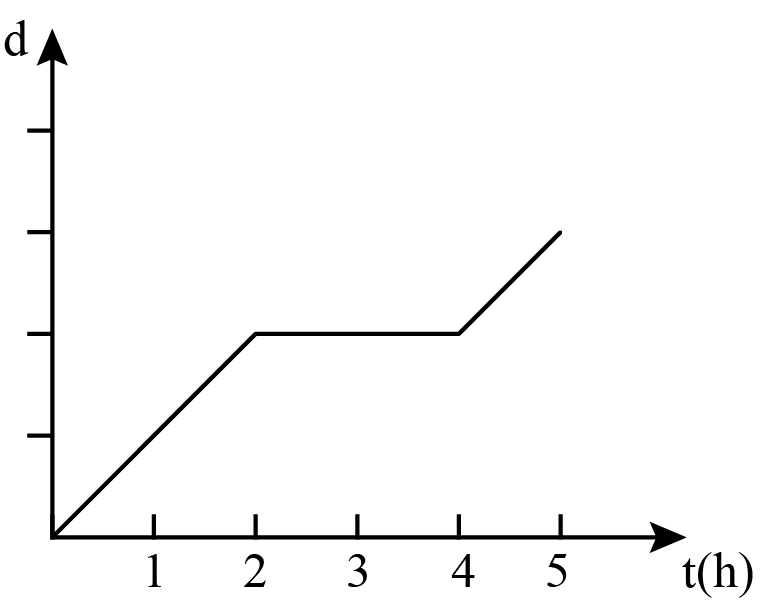
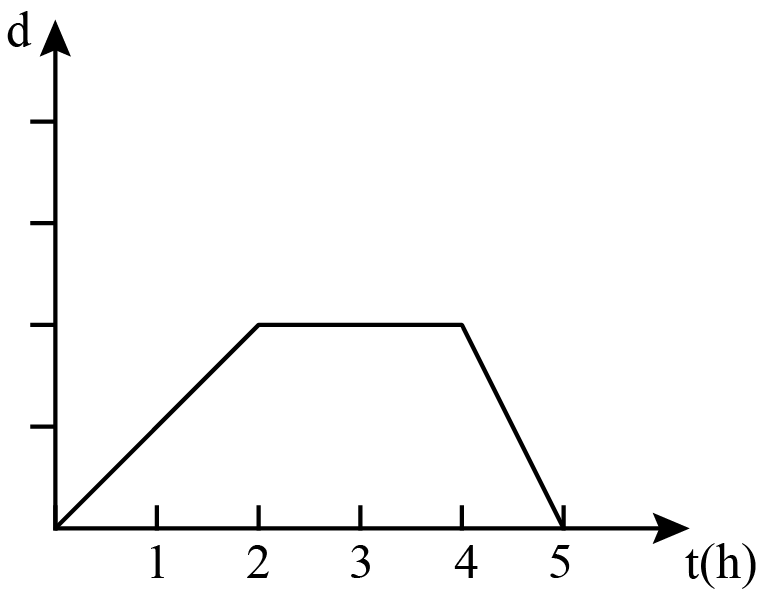
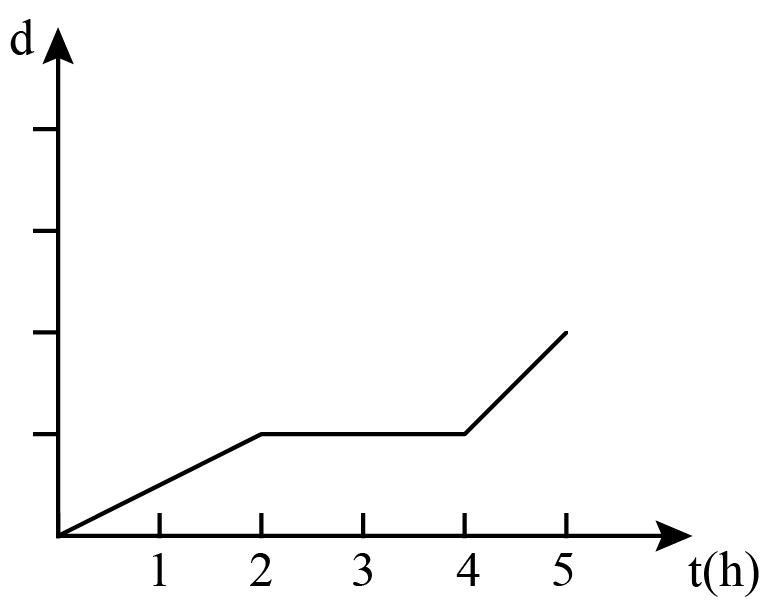
Yesterday was Saturday. Alice set out from home to see her grandmother. She walked for two hours in a straight line at a fixed speed. After arriving at grandmother's home, Alice spent two hours eating lunch and chatting with her. Then Alice took the bus back home. Taking the bus is twice as fast as walking. During the process, the relationship between Alice's distance from home (d) and time (t) is .
- A.
- B.
- C.
- D.
- E.
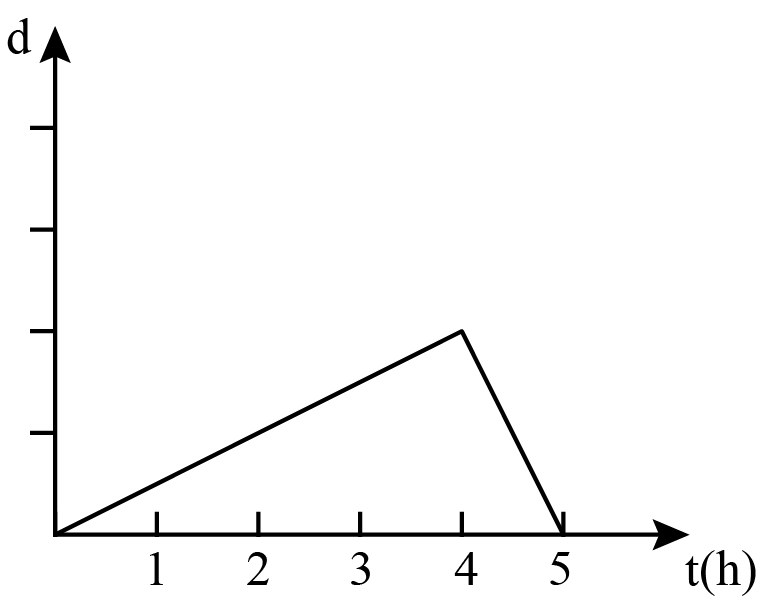
In the first two hours, Alice walked to her grandma's home, then she stayed in grandma's house for two hours. Starting from , she took the bus back home and the speed was twiced. So the answer is .
- 1
- 2
- 3
- 4
- 5
