AMC 8 Daily Practice Round 2
Complete problem set with solutions and individual problem pages
Sara had ten dollars for lunch. She bought a hamburger, a salad, and a cup of apple juice for , , and dollars, respectively. How many dollars did she have after lunch?
- A.
- B.
- C.
- D.
- E.
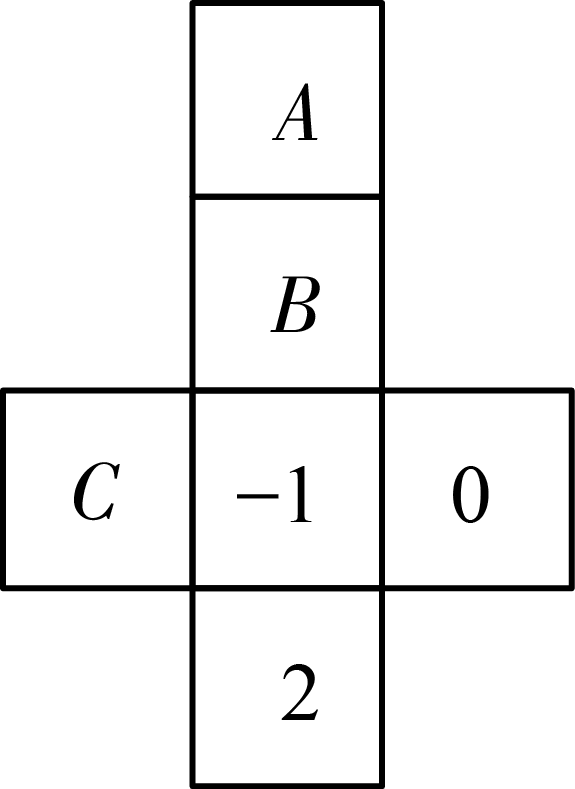
As the figure shown, this is a net of a cube. Fill appropriate numbers in three squares , , and , so that the sum of two numbers on the opposite faces after folding into a cube is . Then the three numbers filled in the squares , , and are , respectively.
- A.
- B.
- C.
- D.
- E.
Pay attention: the sum of opposite number has to be . From the net we can get the answer .
In a class of students, students like to play either basketball, or badminton, or both. If there are students who like to play basketball and students who like to play badminton, how many students like to play both?
- A.
- B.
- C.
- D.
- E.
There are students in the school, and of them are randomly chosen for sampling. The table below shows the range of heights () of the students. Find the range where the median lies.
| Range of Height() | Frequency |
- A.
- B.
- C.
- D.
- E.
According to the definition of median, we need to find the range which the th student and st student lie. The answer is .
The thousands digit of a four-digit number is less than the ones digit. Then reverse all the digits of the four-digit number to get a new number. Then we subtract the original number from the new four-digit number. What is the ones digit of the result after subtraction?
- A.
- B.
- C.
- D.
- E.
Method1: Let the thousands, hundreds, tens, and ones digits of the original four-digit number be , , , and respectively. We are given that . The original four-digit number is equal to . The thousands, hundreds, tens and ones digits of the reversed four-digit number are , , , and , respectively. This number is equal to . Subtracting the original expression from the new one, we get. Thus, the ones digit in the final result is .
Method2:The result must hold for any four-digit number with thousands digit being less than the ones digit. is such a number. Evaluating we get . Thus, the ones digit in the final result is .
- 1
- 2
- 3
- 4
- 5
