2025 AMC 10 A
Complete problem set with solutions and individual problem pages
Andy and Betsy both live in Mathville. Andy leaves Mathyille on his bicycle at , traveling due north at a steady miles per hour. Betsy leaves on her bicycle from the same point at , traveling due east at a steady miles per hour. At what time will they be exactly the same distance from their common starting point?
- A.
- B.
- C.
- D.
- E.
Let represent Betsy's travel time in hours. Then Andy's travel time is hours. Setting up the equation based on distance traveled: , which yields . Therefore, the meeting time is 4:30 PM.
A box contains pounds of a nut mix that is percent peanuts, percent cashews, and percent almonds. A second nut mix containing percent peanuts, percent cashews, and percent almonds is added to the box resulting in a new nut mix that is percent peanuts. How many pounds of cashews are now in the box?
- A.
- B.
- C.
- D.
- E.
Define as the weight (in pounds) of the second mixture.
The proportion of peanuts in the combined mixture satisfies: Therefore, the cashew content equals pounds.
How many isosceles triangles are there with positive area whose side lengths are all positive integers and whose longest side has length ?
- A.
- B.
- C.
- D.
- E.
Consider isosceles triangles with side lengths where .
Scenario 1: .
By triangle inequality: , which gives , so .
Therefore, gives us 1013 valid triangles.
Scenario 2: .
We have , yielding 2025 valid triangles.
Notice that we count the equilateral with side length twice, so the combined total is triangles.
A team of students is going to compete against a team of teachers in a trivia contest. The total number of students and teachers is . Ash, a cousin of one of the students, wants to join the contest. If Ash plays with the students, the average age on that team will increase from to . If Ash plays with the teachers, the average age on that team will decrease from to . How old is Ash?
- A.
- B.
- C.
- D.
- E.
Let denote the number of students, making the number of teachers. Let represent Ash's age.
From the students' average age:
From the teachers' average age:
Solving this system: - From the first equation: - From the second equation:
Therefore , which gives and .
Consider the sequence of positive integers
What is the term in this sequence?
- A.
- B.
- C.
- D.
- E.
Divide the whole sequence at each .
The -th sequence would be: , which has length .
The cumulative length until the end of the -th sequence is:
Computing: and .
Hence, the 2025th term appears at position within the 45th sequence , giving us 45.
In an equilateral triangle each interior angle is trisected by a pair of rays. The intersection of the interiors of the middle -angle at each vertex is the interior of a convex hexagon. What is the degree measure of the smallest angle of this hexagon?
- A.
- B.
- C.
- D.
- E.
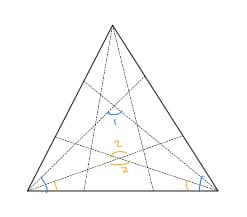
Computing the angles:
By symmetry, the hexagon's six angles are .
Suppose and are real numbers. When the polynomial is divided by , the remainder is . When the polynomial is divided by , the remainder is . What is ?
- A.
- B.
- C.
- D.
- E.
Define .
Using the given conditions: - -
This gives us: - -
Solving: and .
Consequently, .
Agnes writes the following four statements on a blank piece of paper.
At least one of these statements is true.
At least two of these statements are true.
At least two of these statements are false.
At least one of these statements is false.
Each statement is either true or false. How many false statements did Agnes write on the paper?
- A.
- B.
- C.
- D.
- E.
Denote the four statements as . Let and represent the counts of true and false statements respectively. We know .
Assume is false. This implies , which would make false—a contradiction!
Since at least one of (or pick ) is true, at least one of (or pick ) is true, we have , confirming are true.
If were false, then , contradicting 's falsity!
Hence, is true, yielding , which implies is false, with .
Let . For how many real numbers does the graph of pass through the point ?
- A.
- B.
- C.
- D.
- E.
more than
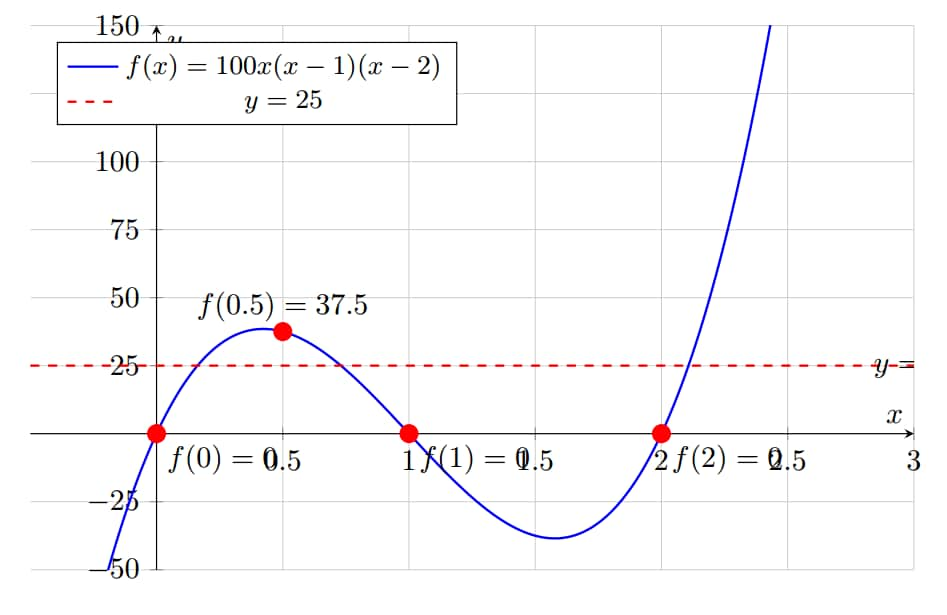
We seek the number of solutions of , which is equivalent to the number of solutions of .
Since , we have . As the coefficient of is positive, we can draw the diagram of .
Note that
By the intermediate value theorem, there exist and satisfying .
Since and , there exists with .
As is a cubic equation with at most 3 real roots, are all the solutions.
A semicircle has diameter and chord of length parallel to . A smaller semicircle with diameter on and tangent to is cut from the larger semicircle, as shown below.
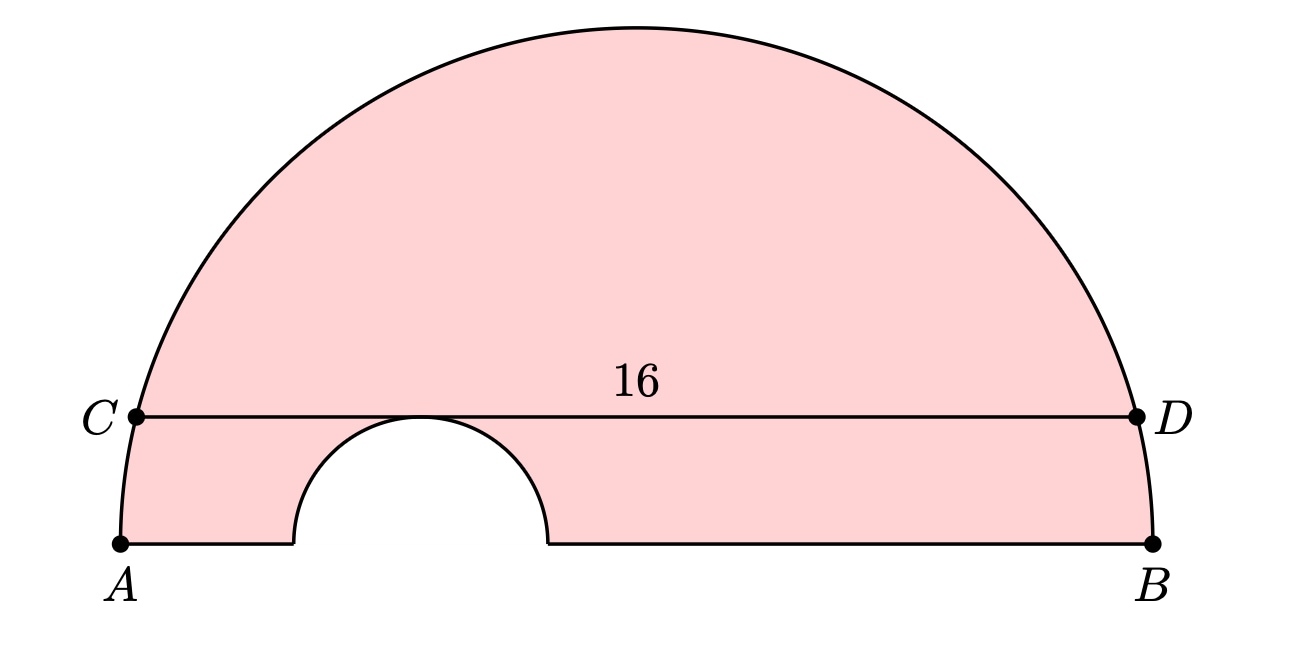
What is the area of the resulting figure, shown shaded?
- A.
- B.
- C.
- D.
- E.
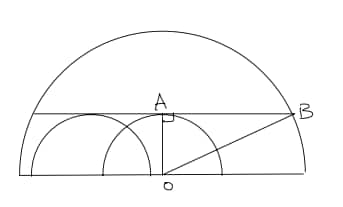
Let and denote the radii of the smaller and larger semicircles respectively.
As in the diagram, we can translate the tangent smaller semi-circle to be centered at O. So , , and . Thus .
The answer is:
The sequence is arithmetic. The sequence is geometric. Both sequences are strictly increasing and contain only integers, and is as small as possible. What is the value of
- A.
- B.
- C.
- D.
- E.
Let be the common difference and be the common ratio, where with .
The equation holds. Since , we have , implying .
For : , yielding .
Carlos uses a -digit passcode to unlock his computer. In his passcode, exactly one digit is even, exactly one (possibly different) digit is prime, and no digit is . How many -digit passcodes satisfy these conditions?
- A.
- B.
- C.
- D.
- E.
Scenario 1: The digit 2 serves as both prime and even. The remaining digits must be odd and not prime, thus they are in .
With 4 positions for 2, the count is .
Scenario 2: Excluding 2, the prime comes from , the even digit from , and others from . There are arrangements for prime and even positions.
The count is .
Total count: .
The ratio of the side length of a square to the side length of the next inner square is , where . The area of the shaded portion of the figure is % of the area of the original square. What is ?

- A.
- B.
- C.
- D.
- E.
Solution 1:
Notice that, the shaded area and the non-shaded area are also similar, with the length ratio , and therefore an area ratio .
Thus the shaded area is , giving .
Solution 2:
The total area forms an infinite geometric series:
Setting yields .
Six chairs are arranged around a round table. Two students and two teachers randomly select four of the chairs to sit in. What is the probability that the two students will sit in two adjacent chairs and the two teachers will also sit in two adjacent chairs?
- A.
- B.
- C.
- D.
- E.
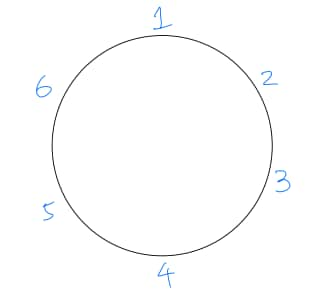
We may label the six seats as on a round table.
Choose the two seats for the two students (order of the two students does not matter).
There are unordered choices in total, while the adjacent pairs are , hence choices. Therefore
Given that the students are adjacent, without loss of generality, suppose they occupy seats . The remaining seats are . Among these four, the adjacent pairs (on the circle) are , so there are favorable pairs for the two teachers out of unordered choices. Thus
Thus the final answer is
In the figure below, is a rectangle, , , , and .
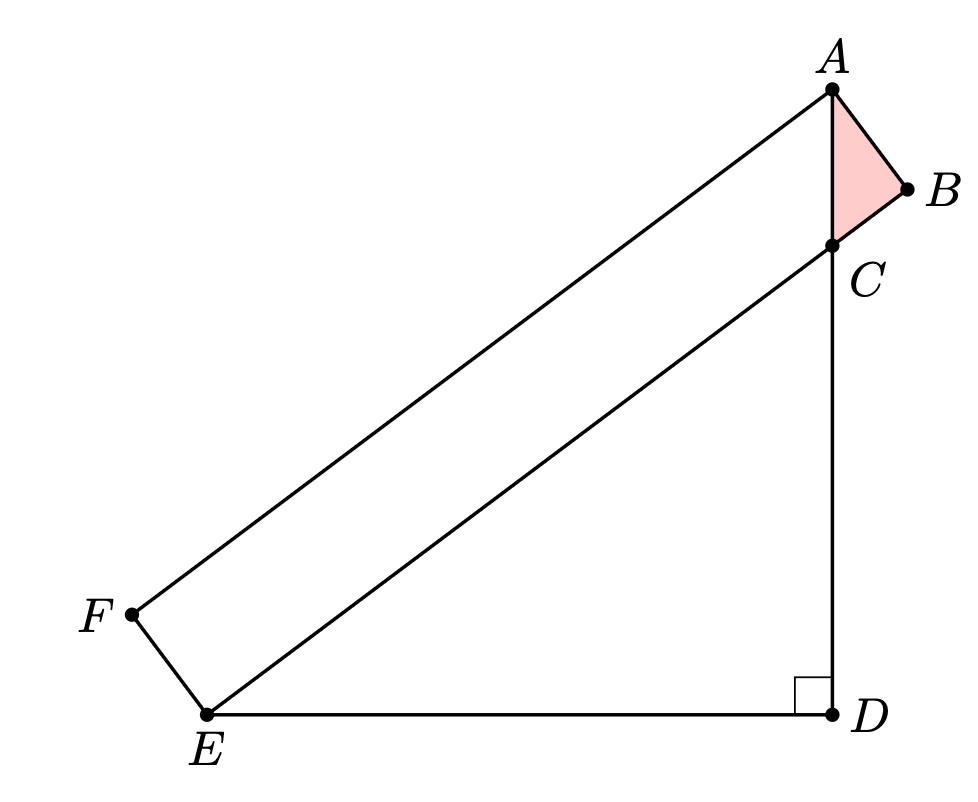
What is the area of ?
- A.
- B.
- C.
- D.
- E.
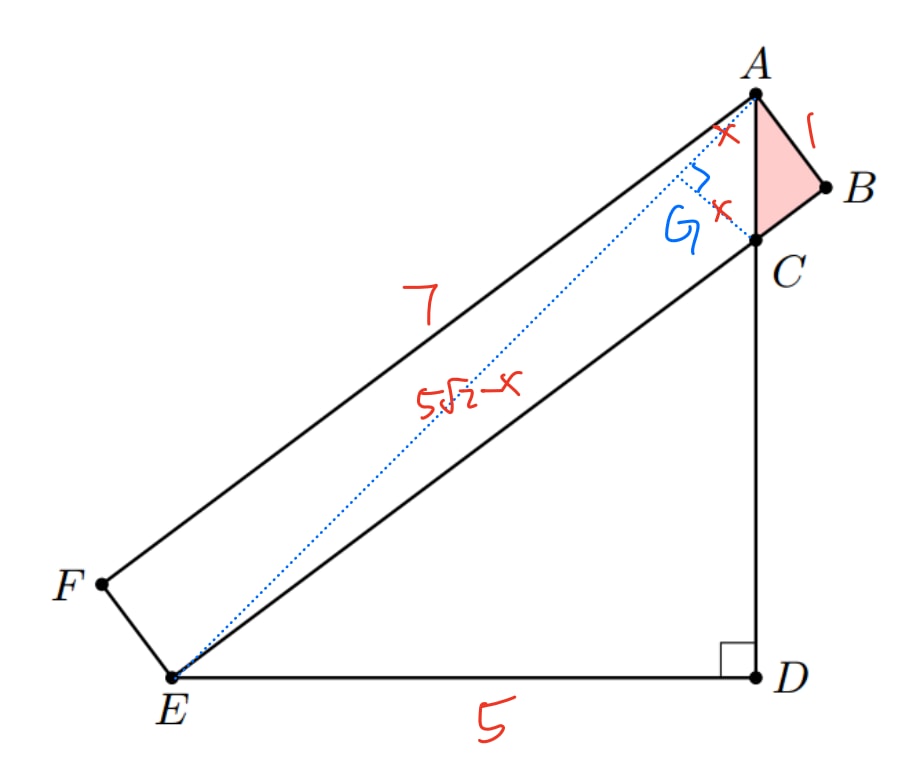
By Pythagorean theorem, we can see that , . So is a right isoceles triangle, .
Make altitude at G. Set , then . As ,
So . Area calculation:
There are three jars. Each of three coins is placed in one of the three jars, chosen at random and independently of the placements of the other coins. What is the expected number of coins in a jar with the most coins?
- A.
- B.
- C.
- D.
- E.
Total arrangements for placing 3 coins in 3 jars: .
If maximum coins per jar = 1: Each jar contains exactly one coin. Count: .
If maximum coins per jar = 3: One jar holds all coins. Count: .
Remaining arrangements (): One jar has 2 coins, another has 1.
Expected maximum:
Let be the unique positive integer such that dividing by leaves a remainder of and dividing by leaves a remainder of . What is the tens digit of ?
- A.
- B.
- C.
- D.
- E.
Since is unique, we know that
Therefore, .
Since and noting , we deduce . As , we have .
The harmonic mean of a collection of numbers is the reciprocal of the arithmetic mean of the reciprocals of the numbers in the collection. For example, the harmonic mean of , , and is
What is the harmonic mean of all the real roots of the 4050th degree polynomial
- A.
- B.
- C.
- D.
- E.
Let and denote the roots of .
By Vieta's formulas:
Summing over all values:
Computing the required expression:
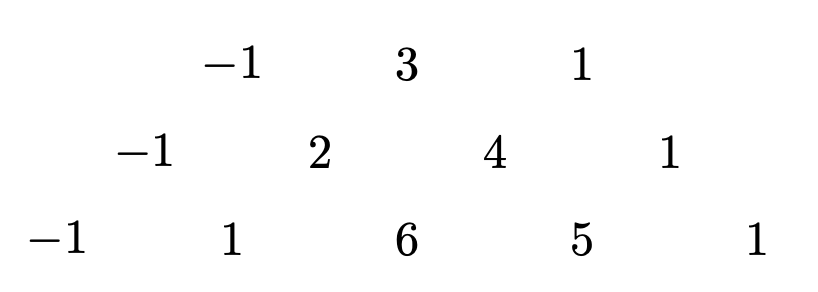
- A.
- B.
- C.
- D.
- E.
Let represent the sum of row . Since all the numbers in row can be seen as the sum of the two numbers above it (one number above for the leftmost and rightmost ), we have the recurrence relation , yielding . As , it is the sum of the 13-th row.
Define as the second element of row , and as the third element.
From the pattern: with , which gives for .
With and :
Therefore, .
A silo (right circular cylinder) with diameter meters stands in a field. MacDonald is located meters west and meters south of the center of the silo. McGregor is located meters east and meters south of the center of the silo. The line of sight between MacDonald and McGregor is tangent to the silo. The value of g can be written as , where and are positive integers, is not divisible by the square of any prime, and is relatively prime to the greatest common divisor of and . What is ?
- A.
- B.
- C.
- D.
- E.
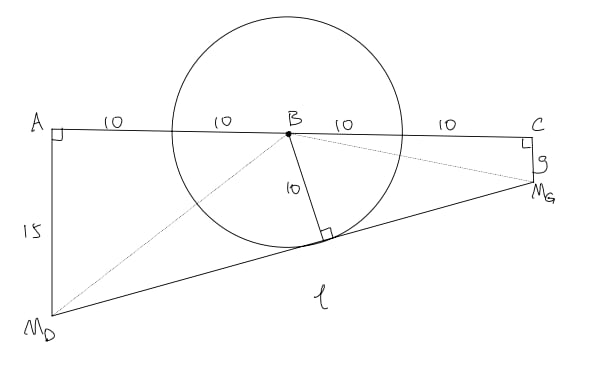
Let denote the distance between points and . The trapezoid's area is:
Also, trapezoid area = .
Equating: gives .
Using the Pythagorean theorem: .
Expanding:
This simplifies to .
Applying the quadratic formula:
Since : .
A set of numbers is called if whenever and are (not necessarily distinct) elements of the set, is not an element of the set. For example, {} and the empty set are sum-free, but {} is not. What is the greatest possible number of elements in a sum-free subset of {}?
- A.
- B.
- C.
- D.
- E.
The set forms a sum-free subset with elements.
Suppose there exists a sum-free subset of elements, with the largest element. Then the differences for are all distinct from .
Moreover, these differences are mutually distinct. The union of the 10 differences and the 11 original elements would form a 21-element subset of , which is a contradiction.
A circle of radius r is surrounded by three circles, whose radi are , , and , all externally tangent to the inner circle and externally tangent to each other, as shown in the diagram below.

What is ?
- A.
- B.
- C.
- D.
- E.

Let denote the centers of the three circles, with as the small circle's center.
Since , we have .
Establish coordinates: .
Let . Since : - Equation (1): - Equation (2): - Equation (3):
From equations (1) and (2): .
From equations (1) and (3): .
Substituting into (1):
This simplifies to , giving or .
Since : .
Triangle has side lengths , , and . The bisector of and the altitude to side intersect at point . What is ?
- A.
- B.
- C.
- D.
- E.
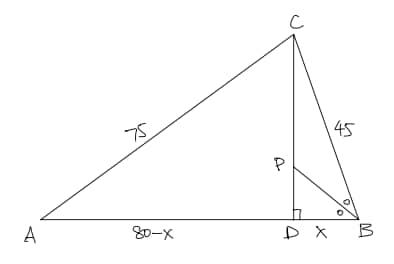
Set , making .
This gives .
Solving: , and , so .
By the angle bisector theorem,
So
Therefore:
Thus .
Call a positive integer if no digit is used more than once, it has no s, and no digit ins adjacent to two greater digits. For example, , , and are fair, but , , and are not fair. How many fair positive integers are there?
- A.
- B.
- C.
- D.
- E.
For selected digits, let count arrangements where no digit is adjacent to two larger digits.
Base cases: .
For , the smallest digit must occupy either the first or last position.
Each placement corresponds bijectively to arranging digits with the same constraint, giving , hence .
Total fair integers:
A point is chosen at random inside square . The probability that is neither the shortest nor the longest side of can be written as , where , and are positive integers, , and is not divisible by the square of any prime. What is ?
- A.
- B.
- C.
- D.
- E.
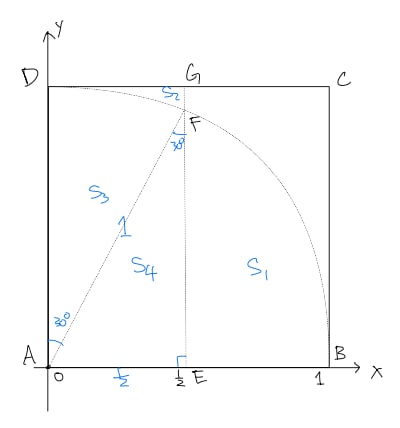
Establish coordinates: .
Scenario 1: . For point :
Condition implies , and condition implies .
Point lies within the unit circle centered at and to the right of which is . This defines region .
Scenario 2: .
Condition implies , and condition implies .
Point lies outside the unit circle and to the left of . This defines region .
Mark and as in the diagram too. Notice that and . So
Thus , and .
Also , and .
Final result:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
