2022 AMC 10 A
Complete problem set with solutions and individual problem pages
Mike cycled laps in minutes. Assume he cycled at a constant speed throughout. Approximately how many laps did he complete in the first minutes?
- A.
- B.
- C.
- D.
- E.
Assume the number of laps is .
.
The sum of three numbers is . The first number is times the third number, and the third number is less than the second number. What is the absolute value of the difference between the first and second numbers?
- A.
- B.
- C.
- D.
- E.
Assume is the third number.
In some countries, automobile fuel efficiency is measured in liters per kilometers while other countries use miles per gallon. Suppose that kilometer equals miles, and gallon equals liters. Which of the following gives the fuel efficiency in liters per kilometers for a car that gets miles per gallon?
- A.
- B.
- C.
- D.
- E.
= = = .
Square has side length . Point , , , and each lie on a side of such that is an equilateral convex hexagon with side length . What is ?
- A.
- B.
- C.
- D.
- E.
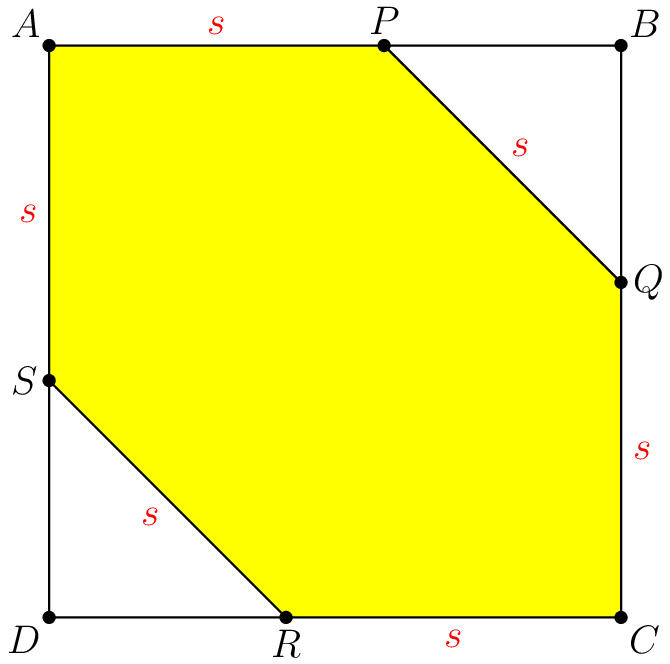
Assume .
, ,
is an isosceles right triangle.
.
The least common multiple of a positive integer and is , and the greatest common divisor of and is . What is the sum of the digits of ?
- A.
- B.
- C.
- D.
- E.
and ,
( is a factor of ).
,
and ,
If you factorize , there is only one factor ,
.
A data set consists of (not distinct) positive integers: , , , , , and . The average (arithmetic mean) of the numbers equals a value in the data set. What is the sum of all positive values of ?
- A.
- B.
- C.
- D.
- E.
The possible values for the mean: .
If mean , ;
If mean =7, ;
If mean =x, , then .
Sum .
A rectangle is partitioned into regions as shown. Each region is to be painted a solid color - red, orange, yellow, blue, or green - so that regions that touch are painted different colors, and colors can be used more than once. How many different colorings are possible?
- A.
- B.
- C.
- D.
- E.
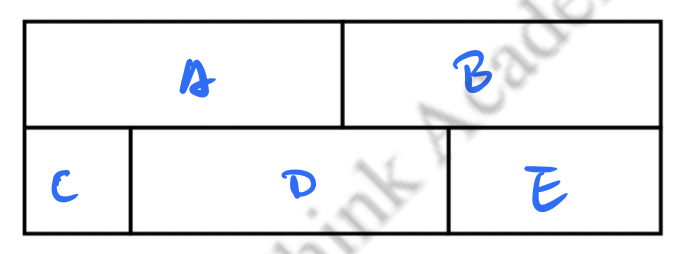
is special as it touches all the other rectangles.
Step : Paint first, we have choices;
Step : Paint , we have choices;
Step : Paint , we have choices (it's different from );
Step : Paint and at last, we have choices for each.
Total number of ways .
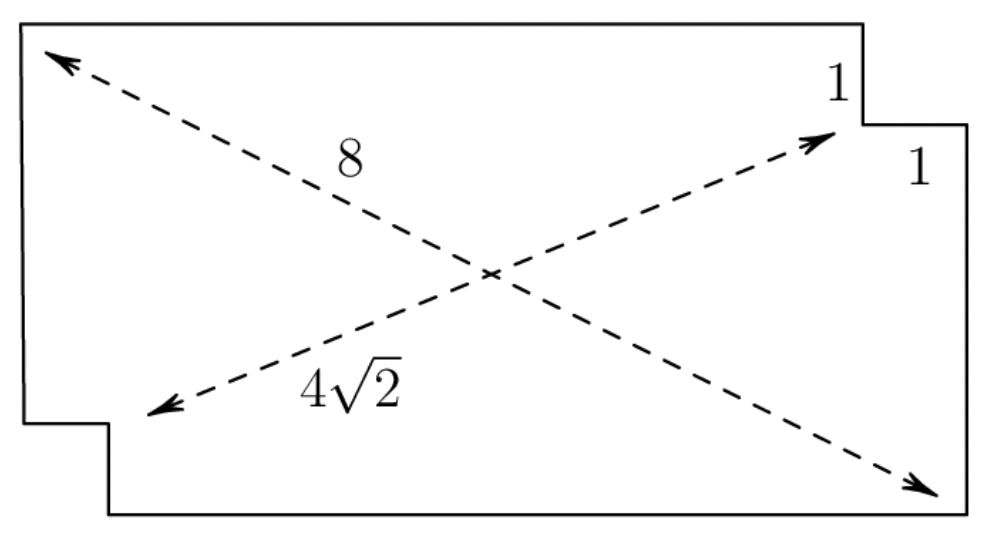
Daniel finds a rectangular index card and measures its diagonal to be centimeters. Daniel then cuts out equal squares of side cm at two opposite cormers of the index card and measures the distance between the two closest vertices of these squares to be centimeters, as shown below. What is the area of the original index card?
- A.
- B.
- C.
- D.
- E.
Assume the length of the index is and the width is .
Area
Ted mistakenly wrote , as . What is the sum of all real numbers for which these two expressions have the same value?
- A.
- B.
- C.
- D.
- E.
Using Vieta's formula, sum of roots .
On Halloween children walked into the principal's office asking for candy. They can be classified into three types: Some always lie; some always tell the truth; and some alternately lie and tell the truth. The alternaters arbitrarily choose their first response, either a lie or the truth, but each subsequent statement has the opposite truth value from its predecessor. The principal asked everyone the same three questions in this order.
"Are you a truth-teller?" The principal gave a piece of candy to each of the children who answered yes.
"Are you an alternater?" The principal gave a piece of candy to each of the children who answered yes.
"Are you a liar?" The principal gave a piece of candy to each of the children who answered yes.
How many pieces of candy in all did the principal give to the children who always tell the truth?
- A.
- B.
- C.
- D.
- E.
Answer (A): Let denote the number of truth-tellers, the number of alternators who tell the truth on odd-numbered questions, the number of alternators who tell the truth on evennumbered questions, and the number of liars. These four variables must satisfy the following equations.
Subtract the third equation from the second to find that . Because they received candy only in response to the first question, they received 7 pieces of candy. Note: It may be further deduced from the system of equations that , and .
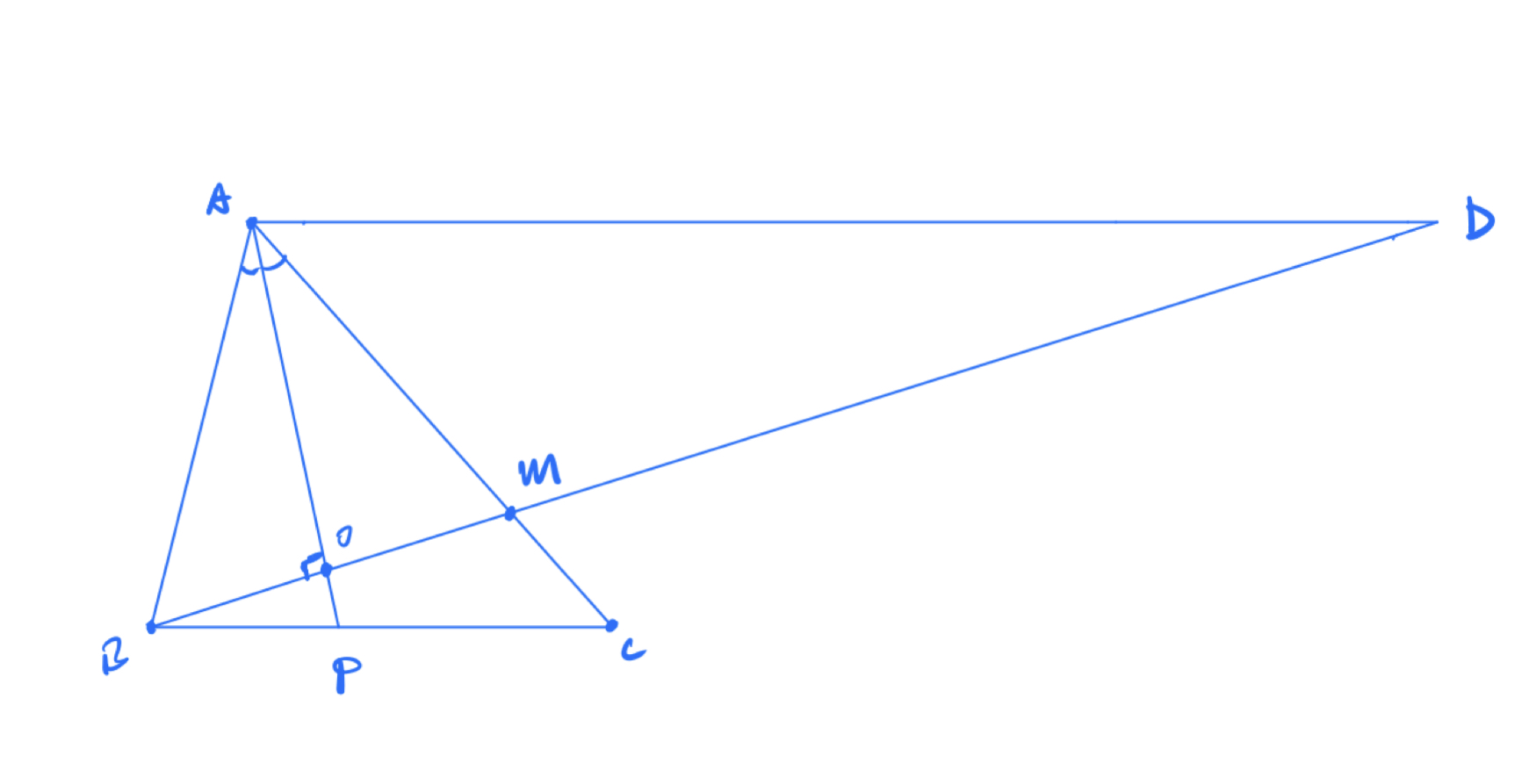
Let be a scalene triangle. Point lies on so that bisects . The line through perpendicular to intersects the line through parallel to at point . Suppose and . What is ?
- A.
- B.
- C.
- D.
- E.
How many ways are there to split the integers through into pairs such that in each pair, the greater number is at least times the lesser number?
- A.
- B.
- C.
- D.
- E.
Integers from to have to be separated into differentt groups, because none of them could be the 'lesser number' in the pair to be the larger number. The lesser number candidates are .
(let's go with )
(let's go with )
(let's go with )
(let's go with )
(let's go with )
Quadrilateral with side lengths , , , is inscribed in a circle. The area interior to the circle but exterior to the quadrilateral can be written in the form , where , , and are positive integers such that and have no common prime factor. What is ?
- A.
- B.
- C.
- D.
- E.
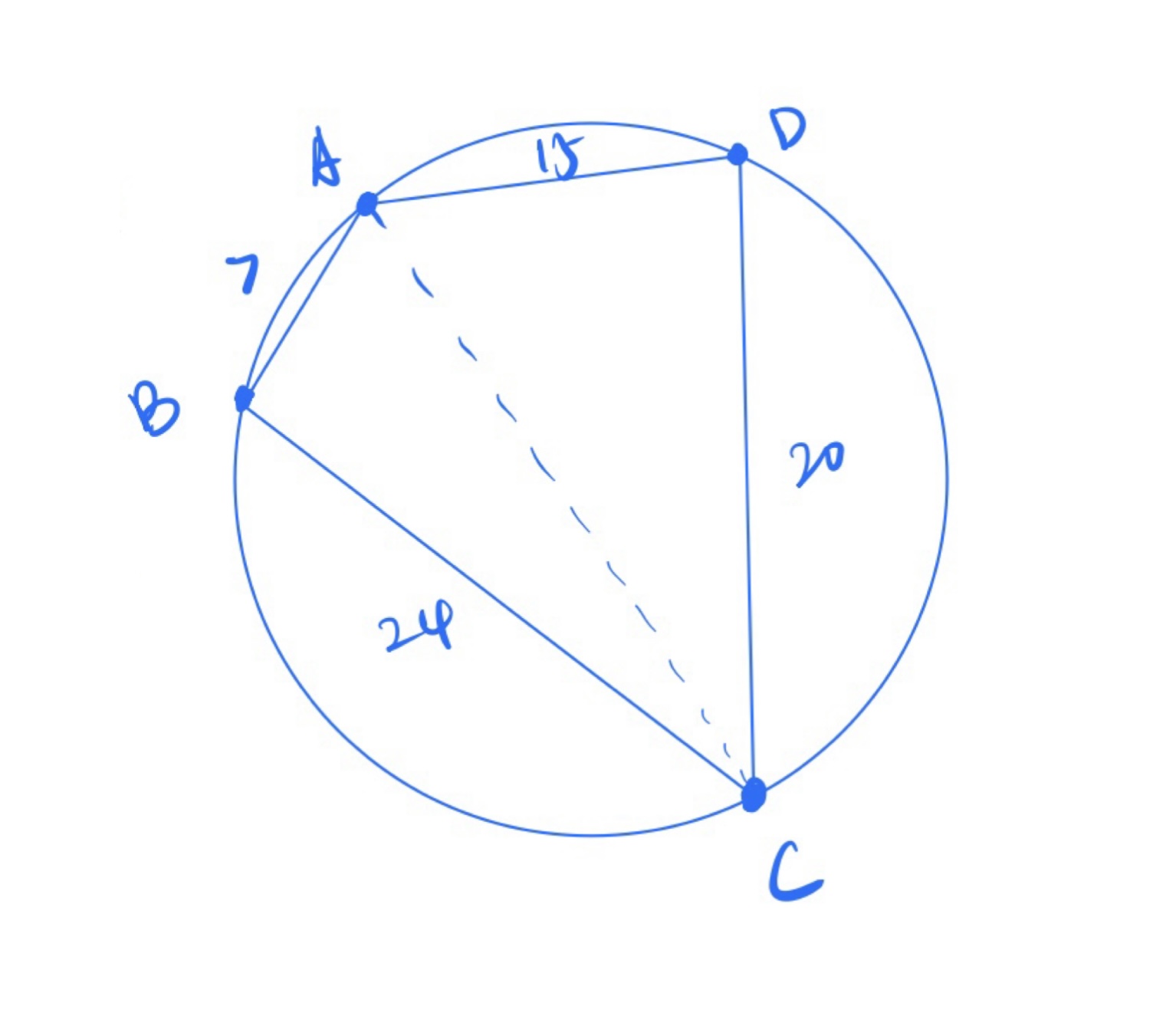
If
, so there is a contradiction.
If , we also have a contradiction.
,
AC is the diameter of the circle.
,
.
.
The roots of the polynomial are the height, length, and width of a rectangular box (right rectangular prism). A new rectangular box is formed by lengthening each edge of the original box by units. What is the volume of the new box?
- A.
- B.
- C.
- D.
- E.
Assume the roots of the polynomial are .
According to Vieta's formula,
.
How many three-digit positive integers are there whose nonzero digits , , and satisfy
?
(The bar indicates repetition, thus is the infinite repeating decimal )
- A.
- B.
- C.
- D.
- E.
is a recuesive decimal, so as , and .
.
Thus, either or . Each of these will have an unique solution, yielding the intergers: .
Therefore, the answer is .
Let be the transformation of the coordinate plane that first rotates the plane degrees counterclockwise around the origin and then reflects the plane across the -axis. What is the least positive integer such that performing the sequence of transformations returns the point back to itself?
- A.
- B.
- C.
- D.
- E.
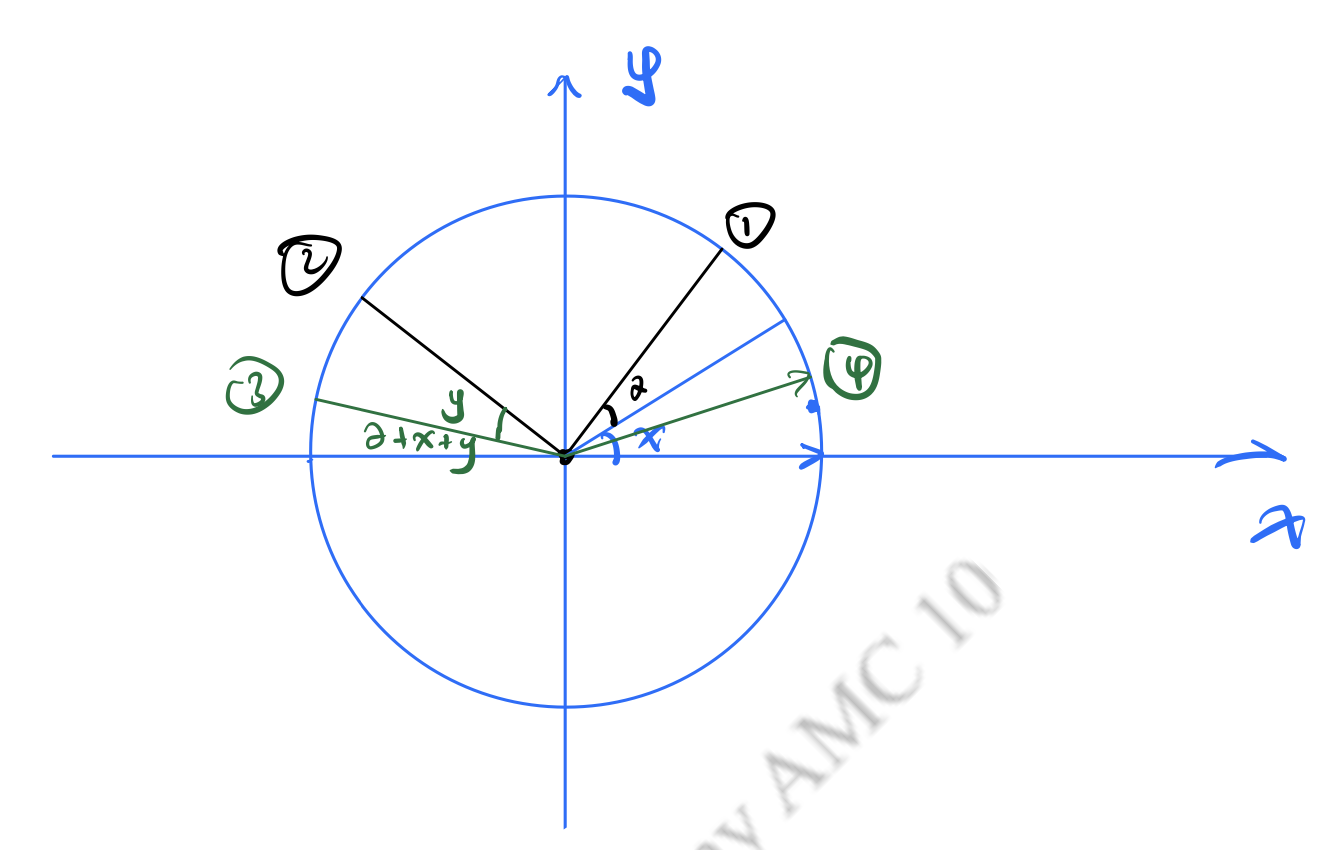
Let the angle between 'the point', 'the origin' and the positive -axis be .
Initially: after .
When , the angle:
.
Back to the original position: , .
When , the angle:
When , .
Define as the least common multiple of all the integers from to inclusive. There is a unique integer such that . What is the remainder when is divided by ?
- A.
- B.
- C.
- D.
- E.
Rearrange:
Every term above is divisible by .
A four-term sequence is formed by adding each term of a four-term arithmetic sequence of positive integers to the corresponding term of a four-term geometric sequence of positive integers.
The first three terms of the resulting four-term sequence are , , and . What is the fourth term of this sequence?
- A.
- B.
- C.
- D.
- E.
Arithematic sequence: .
Geometric sequence: .
Then,
So,
Since is an integer, has factor of .
Let ( is an interger), .
,
or .
When , .
Arithematic sequence: .
Geometric sequence: .
.
When , .
Arithematic sequence: .
Geometric sequence: (contradiction).
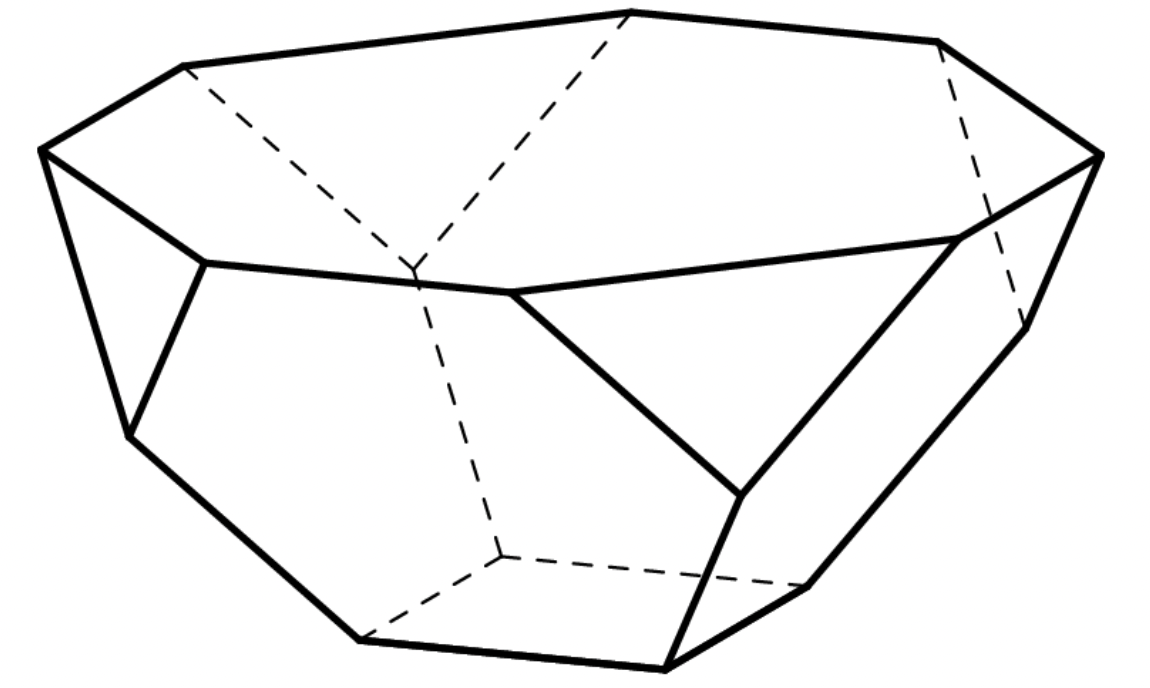
A bowl is formed by attaching four regular hexagons of side to a square of side . The edges of the adjacent hexagons coincide, as shown in the figure. What is the area of the octagon obtained by joining the top eight vertices of the four hexagons, situated on the rim of the bowl?
- A.
- B.
- C.
- D.
- E.
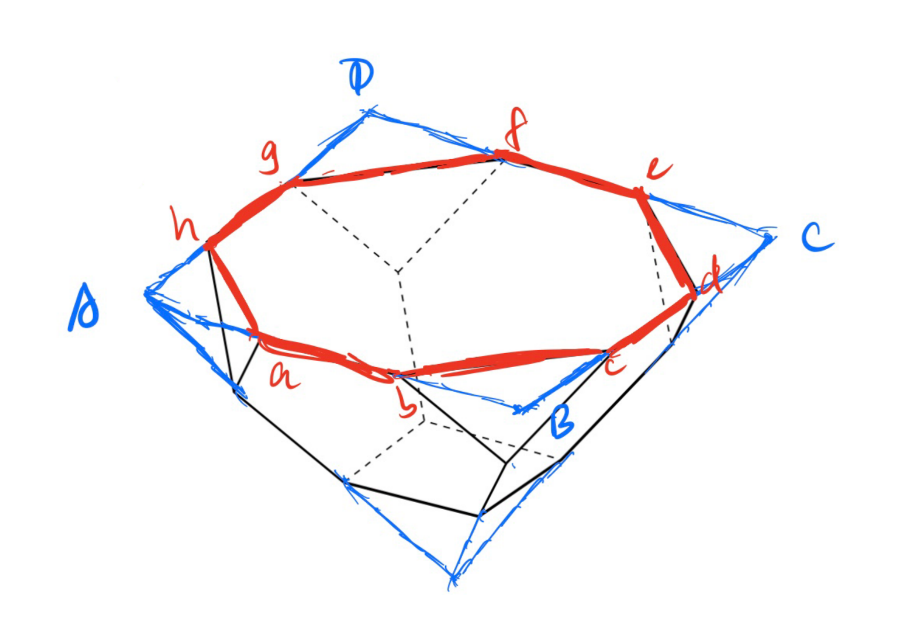
Create an tetraledron, each side of the tetraledron gives an equilateral triangle.
, .
Suppose that cards numbered , , ,, are arranged in a row. The task is to pick them up in numerically increasing order, working repeatedly from left to right. In the example below, cards , , are picked up on the first pass, and on the second pass, on the third pass , , , on the fourth pass, and , , on the fifth pass. For how many of the ! possible orderings of the cards will the cards be picked up in exactly two passes?
![]()
- A.
- B.
- C.
- D.
- E.
Picking up in exactly two passes is equivalent to cutting cards in half.
For example, .
When we rearrange, we need to make sure are arranged in increasing order, but we cannot include the one pass .
:
(Note: there are possible spot for , but we need to subtract the situation when [1] is at the first place.)
:
:
In total: .
Isosceles trapezoid has parallel sides and , with and .
There is a point in the plane such that , and . What is ?
- A.
- B.
- C.
- D.
- E.
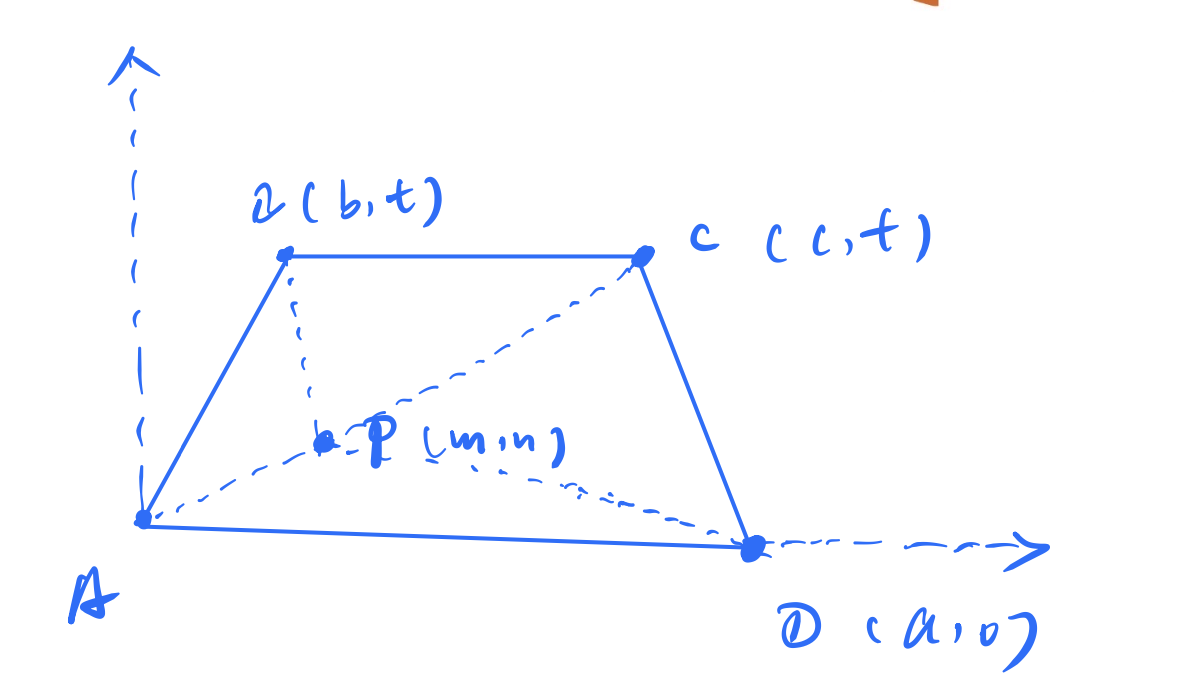
So
Since is equilateral triangle, so .
Thus, .
How many strings of length formed from the digits , , , , are there such that for each , at least of the digits are less than ? (For example, satisfies the condition because it contains at least digit less than , at least digits less than , at least digits less than , and at least digits less than . The string does not satisfy the condition because it does not contain at least digits less than .)
- A.
- B.
- C.
- D.
- E.
Suppose . Then let's do the casework.
① If numbers are all distinct, .
② If one number is counted twice, .
③ If two numbers are counted twice, .
④ If one number is counted times, .
⑤If one number is counted times and the others are counted twice, .
⑥ If one number is counted times, .
⑦ If one number is counted times, only 1 possible way.
In total, .
Let , , and be squares that have vertices at lattice points (i.e. points whose coordinates are both integers) in the coordinate plane, together with their interiors. The bottom edge of each square is on the -axis. The left edge of and the right edge of are on the -axis, and contains as many lattice points as does . The top two vertices of are in , and contains of the lattice points contained in . See the figure (not drawn to scale).
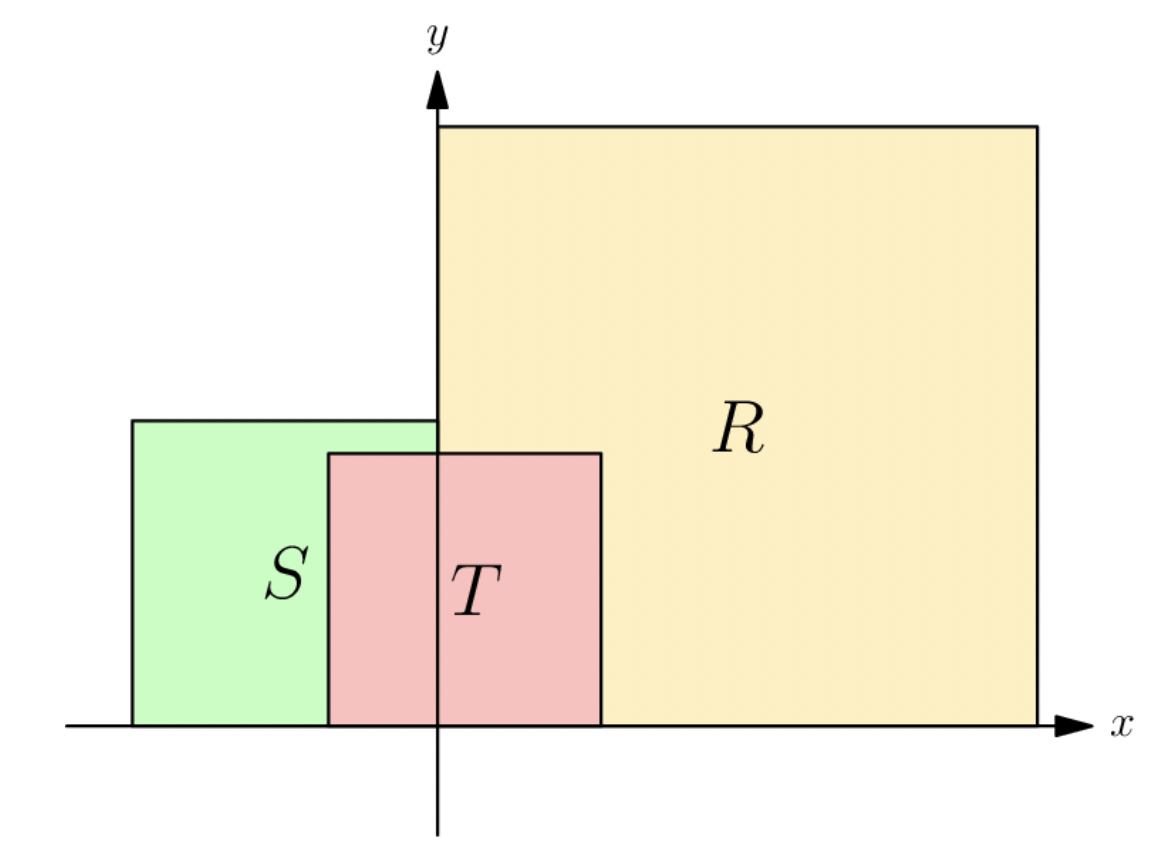
The fraction of lattice points in that are in is times the fraction of lattice points in that are in . What is the minimum possible value of the edge length of plus the edge length of plus the edge length of ?
- A.
- B.
- C.
- D.
- E.
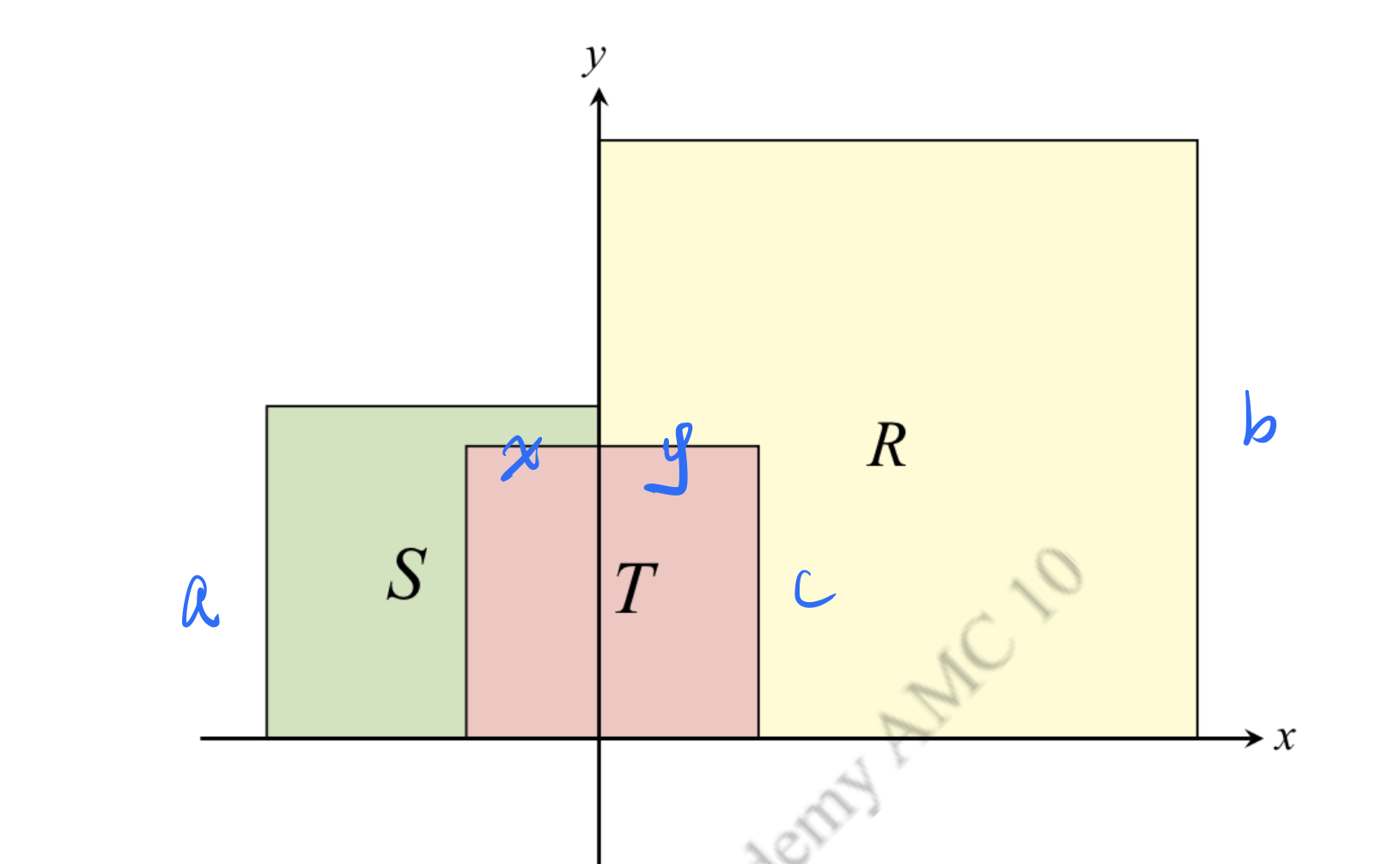
①
②
③
Then
When , .
The equation: has integer solution.
, , so .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25

