2022 AMC 10 B
Complete problem set with solutions and individual problem pages
Define to be for all real numbers and . What's the value of
- A.
- B.
- C.
- D.
- E.
Original Expression
.
In rhombus , point lies on segment such that , and . What is the area of ? (Note: The figure is not drawn to scale.)
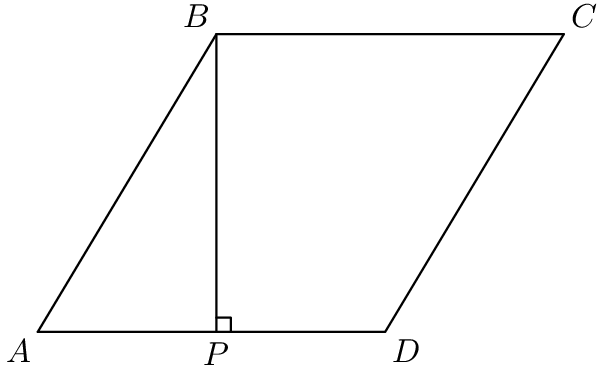
- A.
- B.
- C.
- D.
- E.
is a rhombus, so . is a -- right triangle, hence . The area of the rhombus is base times height: .
A donkey suffers an attack of hiccups and the first hiccup happens at one afternoon. Suppose that the donkey hiccups regularly every seconds. At what time does the donkey's hiccup occur?
- A.
seconds after
- B.
seconds after
- C.
seconds after
- D.
seconds after
- E.
seconds after
The first hiccup at 4 pm needs to be counted. So the hiccup will occur after seconds, or minutes and seconds, which will be seconds after .
How many three-digit positive integers have an odd number of even digits?
- A.
- B.
- C.
- D.
- E.
There are ways to let the number have one even digit, while ways to let the number have three even digits. So the answer is such numbers.
What is the value of
- A.
- B.
- C.
- D.
- E.
Take the difference of squares of the radicand of denominator, we can rewrite the expression in the form of , where and . Here . Substitute and simplify to get the result is .
How many of the first ten numbers of the sequence , , , are prime numbers?
- A.
- B.
- C.
- D.
- E.
Enumerate the terms and find the pattern:
, and so on. Therefore, no numbers in the sequence would be prime.
For how many values of the constant will the polynomial have two distinct integer roots?
- A.
- B.
- C.
- D.
- E.
By Vieta's Formulae, the product of two roots is , which contains factors. Break down to get , and the signs can be reversed. Since we want distinct roots, the case will be neglected, so there are choices of .
Consider the following sets of elements each:
:
.
How many of these sets contain exactly two multiples of ?
- A.
- B.
- C.
- D.
- E.
Note that for each group, there is at least one multiple of and at most two multiples of .
There are multiples of under , while there are groups. Therefore, there are sets contain exactly two multiples of .
The sum can be expressed as , where and are positive integers. What is ?
- A.
- B.
- C.
- D.
- E.
Note that , and therefore this sum is a telescoping sum, which is equivalent to . Our answer is .
Camila writes down five positive integers. The unique mode of these integers is greater than their median, and the median is greater than their arithmetic mean. What is the least possible value for the mode?
- A.
- B.
- C.
- D.
- E.
We have and . If there are three modes, then , which is a contradiction. So there are two modes. Let the five numbers be , respectively, with increasing order. Then and .
, so with .
The five numbers will be .
All the high schools in a large school district are involved in a fundraiser selling T-shirts. Which of the choices below is logically equivalent to the statement "No school bigger than Euclid HS sold more T-shirts than Euclid HS"?
- A.
All schools smaller than Euclid HS sold fewer T-shirts than Euclid HS.
- B.
No school that sold more T-shirts than Euclid is bigger than Euclid HS.
- C.
All schools bigger than Euclid HS sold fewer T-shirts than Euclid HS.
- D.
All schools that sold fewer T-shirts than Euclid HS are samller than Euclid HS.
- E.
All schools smaller than Euclid HS sold more T-shirts than Euclid HS.
In mathematical logics, a contrapositive statement is equivalent to the original statement. We find answer choice is such a statement.
A pair of fair -sided dice is rolled times. What is the least value of such that the probability that the sum of the numbers face up on a roll equals at least once is greater than ?
- A.
- B.
- C.
- D.
- E.
For each roll, the probability to have a sum of is .
To make the probability that the sum of the numbers face up on a roll equals at least once is greater than , we have , where .
The positive difference between a pair of primes is equal to , and the positive difference between the cubes of the two primes is . What is the sum of the digits of the least prime that is greater than those two primes?
- A.
- B.
- C.
- D.
- E.
Let the numbers be and , respectively. Then we have and . With manipulation, and , so and . Observe that and . The next prime number is , so the answer is .
Suppose that is a subset of such that the sum of any two (not necessarily distinct) elements of is never an element of . What is the maximum number of element may contain?
- A.
- B.
- C.
- D.
- E.
The sum of two elements must be at least to avoid overlap with the original set. By this fact, can only pair with , can pair with and , , can pair with all numbers greater than itself up to . Therefore, the set will be the desired set with elements.
Let be the sum of the first term of an arithmetic sequence that has a common difference of . The quotient does not depend on . What is ?
- A.
- B.
- C.
- D.
- E.
.
Since the quotient does not depend on , , and .
The diagram below shows a rectangle with side lengths and and a square with side length . Three vertices of the square lie on three different sides of the rectangle, as shown. What is the area of the region inside both the square and the rectangle?
- A.
- B.
- C.
- D.
- E.
We first notice that the side length of the square is by Pythagorean Theorem. Then, by Triple Perpendicular Model, the four right triangles are similar to each other. . The area of the top right triangle is therefore . Hence the shaded area is .
One of the following numbers is not divisible by any prime number less than . Which is it?
- A.
- B.
- C.
- D.
- E.
A. .
B. .
D. .
E. .
So the answer is C.
Consider systems of three linear equations with unknowns , , and
where each of the coefficients is either or and the system has a solution other than . For example, one such system is with a nonzero solution of . How many such systems are there?(The equations in a system need not be distinct, and two systems containing the same equations in a different order are considered different.)
- A.
- B.
- C.
- D.
- E.
The sufficient and necessary condition for a homogeneous linear system of equations to have a non-zero solution is that the rank of its coefficient matrix is less than the number of unknowns. In simple terms, it means that among these three equations, at least one must be "redundant" and cannot provide additional constraints to solve the equation. It is an identity that always holds true. Then we can discuss the following cases:
One of the equations has coefficients that are all zeros. For each ordered triple of coefficients in the equations , there are a total of choices. So for this case, we have choices.
None of the equations has coefficients that are all zeros and one of the equations can be obtained by linearly combining the other two equations (without loss of generality, we consider only addition).
Among the three equations, there are two equations that are identical. For this case, we have choices.
In the equation that is a "sum", only two coefficients are 1 and the other one is 0. For example, for the ordered triples of coefficients in the equations we have . For this case, we have choices.
In the equation that is a "sum", all of the three coefficients are 1. For example, for the ordered triples of coefficients in the equations we have . For this case, we have choices.
So in total, we have choices.
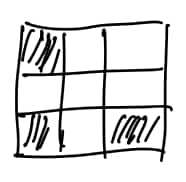
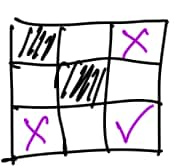
Each square in a grid is either filled or empty, and has up to eight adjacent neighboring squares, where neighboring squares share either a side or a corner. The grid is transformed by the following rules:
-Any filled square with two or three filled neighbors remains filled.
-Any empty square with exactly three filled neighbors becomes a filled square.
-All other squares remain empty or become empty.
A sample transformation is shown in the figure below.
Suppose the grid has a border of empty squares surrounding a subgrid. How many initial configurations will lead to a transformed grid consisting of a single filled square in the center after a single transformation? (Rotations and reflections of the same configuration are considered different.)
- A.
- B.
- C.
- D.
- E.
This is actually a very famous mathematical game called "Conway's Game of Life", which is the most well-known two-dimensional cellular automaton. Its inventor, Professor John Horton Conway, passed away in 2020, and the question writer may have been paying tribute to him in this way.
After discussing the background, let's get back to the problem itself. We will discuss two cases:
The first case is when the central square is initially empty. Therefore, among the eight squares surrounding it, there must be exactly three that are filled.
Its three filled neighbours are all in the corner.
For this case, we have initial configurations.
Two of its three filled neighbours are in the corner.
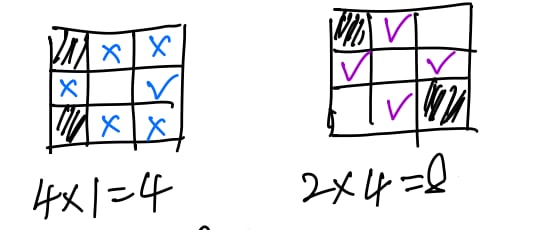
As shown in the diagram, we have initial configurations.
One of its three filled neighbours is in the corner.

As shown in the diagram, we have initial configurations.
None of its three filled neighbours is in the corner. At this point, there must be a filled square with two filled neighbours so that does not hold.
The second case is when the central square is initially filled. Therefore, among the eight squares surrounding it, there must be two or three that are filled.
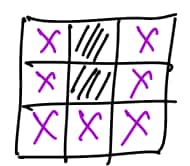
If one of it is not in the corner, then no matter how the other square is placed, there will always be a new filled point generated.
So all points must be in the corners, and at this point, there can only be two filled points and they must be placed in opposite corners. We have initial configurations.
So in total, we have initial configurations.
Let be a rhombus with . Let be the midpoint of , and let be the point on such that is perpendicular to . What is the degree measure of ?
- A.
- B.
- C.
- D.
- E.
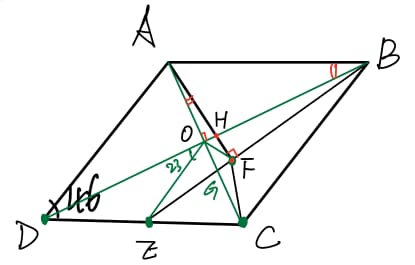
Refer to the figure. and . Denote the intersection between and as . Here is the orthocenter of .
.
∵ ,
∴ are concyclic,
∴ ,
∴ .
Let () be a polynomial with rational coefficients such that when () is divided by the polynomial , the remainder is , and when () is divided by the polynomial the remainder is . There is a unique polynomial of least degree with these two properties. What is the sum of the squares of the coefficients of that polynomial?
- A.
- B.
- C.
- D.
- E.
;
.
Let the remainder of be .
Then .
Simplify to get
So
and .
,
Answer is .
Let be the set of circles in the coordinate plane that are tangent to each of the three circles with equations and . What is sum of the areas of all circles in .
- A.
- B.
- C.
- D.
- E.

There are two circles that are externally tangent to the two small circles and internally tangent to the large circle. Here and . (blue part)
There are two circles that are internally tangent to the concentric circles and externally tangent to the other circle. Here and . (red part)
There are two circles that are internally tangent to the big and non-center circles, but externally tangent to the small center circle. Here and . (green part)
There are two circles that are internally tangent to all three circles. Here and . (brown part)
The sum of area of all circles is .
Ant Amelia starts on the number line at 0 and crawls in the following manner. For , Amelia chooses a time duration and an increment independently and uniformly at random from the interval . During the nth step of the process, Amelia moves units in the positive direction, using up minutes. If the total elapsed time has exceeded minute during the step, she stops at the end of that step; otherwise, she continues with the next step, taking at most steps in all. What is the probability that Amelia's position when she stops will be greater than ?
- A.
- B.
- C.
- D.
- E.
Let and be random variables that are independently and uniformly distributed in the interval . Note that as shown below:
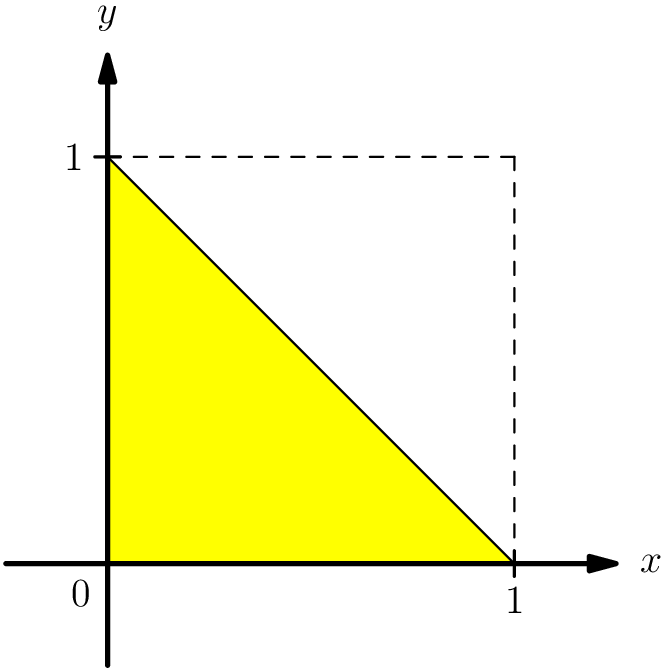
Let , and be random variables that are independently and uniformly distributed in the interval . Note that as shown below:

We have two cases: 1. Amelia takes exactly steps. We need and . So, the probability is .
2. Amelia takes exactly steps. We need and . So, the probability is Together, the answer is (C) .
Consider functions that satisfy for all real numbers and . Of all such functions that also satisfy the equation , what is the greatest possible value of
?
- A.
- B.
- C.
- D.
- E.
;
.
.
Let be a sequence of numbers, where each is either or . For each positive integer , define
Suppose (mod ) for all . What is the value of the sum
?
- A.
- B.
- C.
- D.
- E.
With the patterns, we notice that and . Therefore, .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
