2021 AMC 10 A Fall
Complete problem set with solutions and individual problem pages
What is the value of ?(2021 AMC Fall 10A, Question #1)
- A.
- B.
- C.
- D.
- E.
Solution 1 (Laws of Exponents):
We have
Solution 2 (Difference of Squares) :
We have
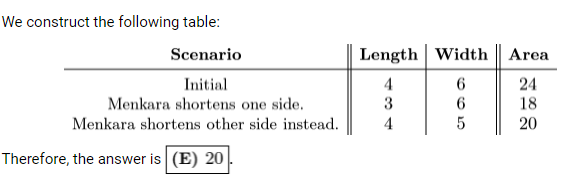
Menkara has a index card. If she shortens the length of one side of this card by inch, the card would have area square inches. What would the area of the card be in square inches if instead she shortens the length of the other side by inch? (2021 AMC Fall 10A, Question #2)
- A.
- B.
- C.
- D.
- E.
What is the maximum number of balls of clay of radius that can completely fit inside a cube of side length assuming the balls can be reshaped but not compressed before they are packed in the cube?(2021 AMC Fall 10A, Question #3)
- A.
- B.
- C.
- D.
- E.
Solution 1:
The volume of the cube is , and the volume of a clay ball is . Since the balls can be reshaped but not compressed, the maximum number of balls that can completely fit inside a cube is Approximating with , we have , or . We simplify to get from which (D) 6 .
Solution 2:
As shown in Solution 1, we conclude that the maximum number of balls that can completely fit inside a cube is . By an underestimation , we have , or . By an overestimation , we have , or . Together, we get from which .
Mr. Lopez has a choice of two routes to get to work. Route is miles long, and his average speed along this route is miles per hour. Route is miles long, and his average speed along this route is miles per hour, except for a -mile stretch in a school zone where his average speed is miles per hour. By how many minutes is Route B quicker than Route A?(2021 AMC Fall 10A, Question #4)
- A.
- B.
- C.
- D.
- E.
Solution 1:
If Mr. Lopez chooses Route , then he will spend hour, or minutes. If Mr. Lopez chooses Route , then he will spend hour, or minutes. Therefore, Route B is quicker than Route A by (B) minutes.
Solution 2:
We use the equation to solve this problem. Recall that 1 mile per hour is equal to mile per minute. For Route A, the distance is 6 miles and the speed to travel this distance is mile per minute. Thus, the time it takes on Route is 12 minutes. For Route , we have to use the equation twice: once for the distance of miles with a speed of mile per minute and a distance of miles at a speed of mile per minute. Thus, the time it takes to go on Route is minutes. Thus, Route is faster than Route A. Thus, the answer is (B) .
The six-digit number is prime for only one digit . What is ? (2021 AMC Fall 10A, Question #5)
- A.
- B.
- C.
- D.
- E.
Solution 1:
First, modulo 2 or . Hence, . Second modulo . Hence, . Third, modulo . Hence, . Therefore, the answer is .
Solution 2:
divisible by divisible by divisible by divisible by divisible by divisible by divisible by divisible by divisible by This leaves only (E) 9 .
Elmer the emu takes equal strides to walk between consecutive telephone poles on a rural road. Oscar the ostrich can cover the same distance in equal leaps. The telephone poles are evenly spaced, and the pole along this road is exactly one mile ( feet) from the first pole. How much longer, in feet, is Oscar's leap than Elmer's stride?(2021 AMC Fall 10A, Question #6)
- A.
- B.
- C.
- D.
- E.
There are gaps between the telephone poles, so the distance of each gap is feet. Each of Oscar's leaps covers feet, and each of Elmer's strides covers feet Therefore, Oscar's leap is feet longer than Elmer's stride.
As shown in the figure below, point lies on the opposite half-plane determined by line from point so that . Point lies on so that , and is a square. What is the degree measure of ?(2021 AMC Fall 10A, Question #7)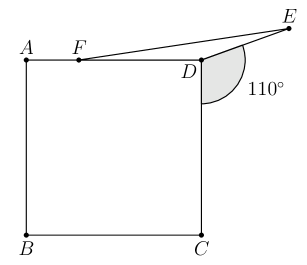
- A.
- B.
- C.
- D.
- E.
By angle subtraction, we have . Note that is isosceles, so . Finally, we get (D) 170 degrees.
A two-digit positive integer is said to be cuddly if it is equal to the sum of its nonzero tens digit and the square of its units digit. How many two-digit positive integers are cuddly?(2021 AMC Fall 10A, Question #8)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Note that the number . By the problem statement, From this we see that must be divisible by 9 . This only happens when . Then, . Thus, there is only cuddly number, which is 89 .
////
Solution 2:
If the tens digit is and the ones digit is then the number is so we have the equation . We can guess and check after narrowing the possible cuddly numbers down to , and 99 . (We can narrow it down to these by just thinking about how 's value affects 's value and then check all the possiblities.) Checking all of these we get that there is only (B) 1 2-digit cuddly number, and it is 89 .
When a certain unfair die is rolled, an even number is times as likely to appear as an odd number. The die is rolled twice. What is the probability that the sum of the numbers rolled is even?(2021 AMC Fall 10A, Question #9)
- A.
- B.
- C.
- D.
- E.
Since an even number is times more likely to appear than an odd number, the probability of an even number appearing is . Since the problem states that the sum of the two die must be even, the numbers must both be even or both be odd. We either have EE or OO, so we have
A school has students and teachers. In the first period, each student is taking one class, and each teacher is teaching one class. The enrollments in the classes are , and . Let be the average value obtained if a teacher is picked at random and the number of students in their class is noted. Let be the average value obtained if a student was picked at random and the number of students in their class, including the student, is noted. What is ?(2021 AMC Fall 10A, Question #10)
- A.
- B.
- C.
- D.
- E.
The formula for expected values is We have Therefore, the answer is .
Emily sees a ship traveling at a constant speed along a straight section of a river. She walks parallel to the riverbank at a uniform rate faster than the ship. She counts equal steps walking from the back of the ship to the front. Walking in the opposite direction, she counts steps of the same size from the front of the ship to the back. In terms of Emily's equal steps, what is the length of the ship?(2021 AMC Fall 10A, Question #11)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Let be the length of the ship. Then, in the time that Emily walks 210 steps, the ship moves steps. Also, in the time that Emily walks 42 steps, the ship moves steps. Since the ship and Emily both travel at some constant rate, . Dividing both sides by 42 and cross multiplying, we get , so , and (A) 70 .
Solution 2:
Let the speed at which Emily walks be steps per hour. Let the speed at which the ship is moving be . Walking in the direction of the ship, it takes her steps, or hours, to travel. We can create an equation: where is the length of the ship. Walking in the opposite direction of the ship, it takes her 42 steps, or hour. We can create a similar equation: Now we have two variables and two equations. We can equate the expressions for and solve for : Therefore, we have (A) 70 .
The base-nine representation of the number is nine. What is the remainder when is divided by ?(2021 AMC Fall 10A, Question #12)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Recall that . We expand by the definition of bases:
Solution 2:
We need to first convert into a regular base- 10 number: Now, consider how the last digit of 9 changes with changes of the power of 9 : Note that if is odd, then On the other hand, if is even, then Therefore, we have Note that for the odd case, may simplify the process further, as given by Solution 1 .
Each of balls is randomly and independently painted either black or white with equal probability. What is the probability that every ball is different in color from more than half of the other balls?(2021 AMC Fall 10A, Question #13)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Note that for this restriction to be true, there must be 3 balls of each color. There are a total of ways to color the balls, and there are ways for three balls chosen to be painted white. Thus, the answer is
Solution 2:
For this restriction to be upheld, there must be three black and three white balls. One such way for this to occur is the arrangement , which has a probability of occuring. However, there are ways to arrange the three black and three white balls, meaning that the answer is, (D)
How many ordered pairs of real numbers satisfy the following system of equations?
- A.
- B.
- C.
- D.
- E.
Solution 1:
The second equation is . We know that the graph of is a very simple diamond shape, so let's see if we can reduce this equation to that form: We now have two separate graphs for this equation and one graph for the first equation, so let's put it on the coordinate plane: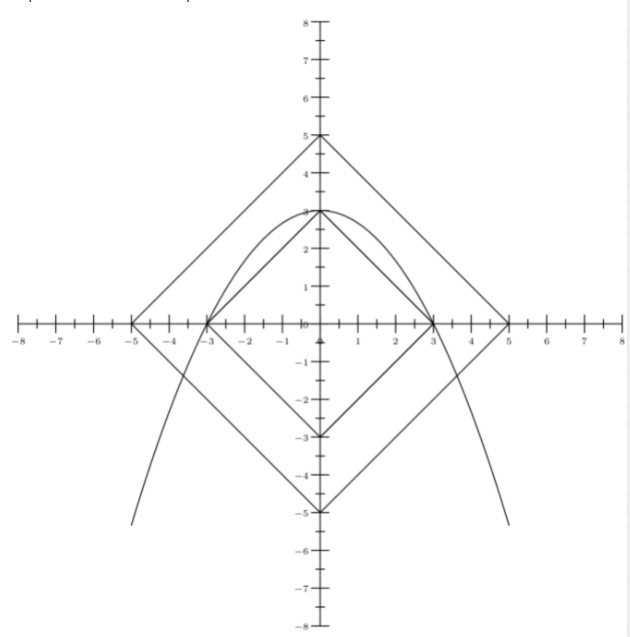
Solution 2:
We can manipulate the first equation to get . From the second equation, we have that or . We will consider each case separately. If , then . The graph of this is a square with vertices , and . The parabola from the first equation is downwards facing, and its vertex is inside this square; the parabola will clearly intersect the square twice. Therefore, this case gives us solutions. If , then . The graph of this is a square with vertices and . The vertex of the parabola from the first equation is on one of the corners of this square (in particular, ). Also, at , the parabola has intercepts of ; the square passes through both of those points. If we continue to move down, the square narrows in, while the parabola continues to expand. Therefore, these are our only 3 intersection points in this case: and . This case gives us solutions. Adding these two cases together, we get our final answer of (D) 5 .
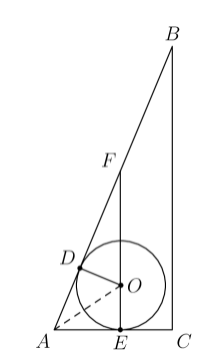
Isosceles triangle has , and a circle with radius is tangent to line at and to line at . What is the area of the circle that passes through vertices , and (2021 AMC Fall 10A, Question #15)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Let be the circle with radius that is tangent to at and to at . Note that . Since the opposite angles of quadrilateral are supplementary, quadrilateral is cyclic. Let be the circumcircle of quadrilateral . It follows that is also the circumcircle of , as shown below:
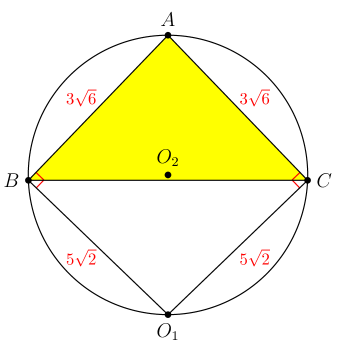
By the Inscribed Angle Theorem, we conclude that is the diameter of . By the Pythagorean Theorem on right , we have Therefore, the area of is .
Solution 2:
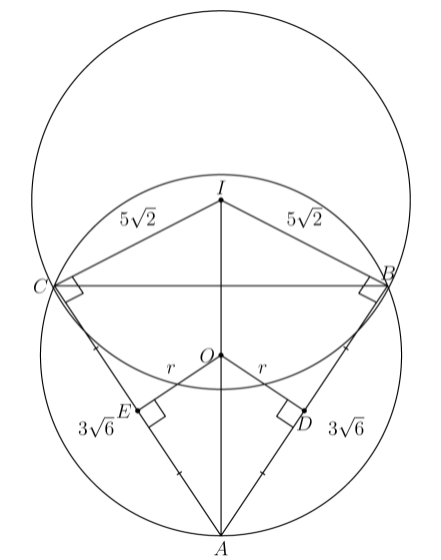
Because circle is tangent to at . Because is the circumcenter of is the perpendicular bisector of , and , so therefore by AA similarity. Then we have . We also know that because of the perpendicular bisector, so the hypotenuse of is This is the radius of the circumcircle of , so the area of this circle is .
The graph of is symmetric about which of the following? (Here is the greatest integer not exceeding (2021 AMC Fall 10A, Question #16)
- A.
the -axis
- B.
the line
- C.
the origin
- D.
the point
- E.
the point
Solution1:
1. and 2. 3. We rewrite as We apply casework to the value of : 1. It follows that . 2. It follows that . 3. It follows that . 4. and It follows that . 5. and It follows that . 6. and It follows that . Together, we have so the graph of is symmetric about (D) the point . Alternatively, we can eliminate (A), (B), (C), and (E) once we finish with Case 3 . This leaves us with (D).
Solution 2:
Denote , where and . Hence, is the integer part of and is the decimal part of .
Case 1: . We have
Case 2: . We have Therefore, the graph of is symmetric through the point . Therefore, the answer is (D) the point
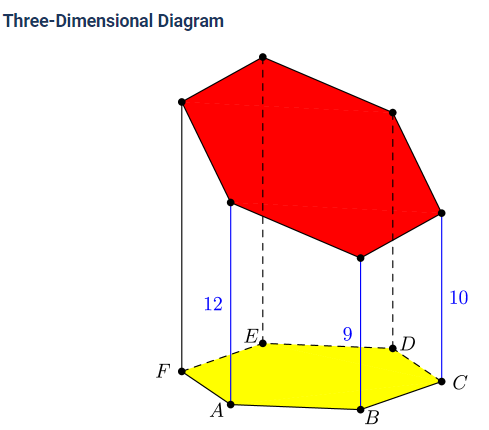
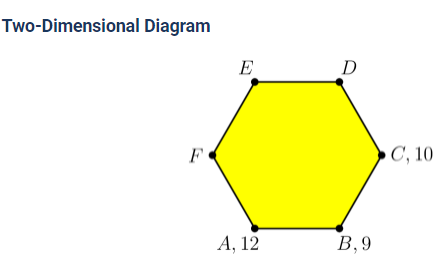
An architect is building a structure that will place vertical pillars at the vertices of regular hexagon , which is lying horizontally on the ground. The six pillars will hold up a flat solar panel that will not be parallel to the ground. The heights of pillars at , and are , and meters, respectively. What is the height, in meters, of the pillar at ?(2021 AMC Fall 10A, Question #17)
- A.
- B.
- C.
- D.
- E.
Solution 1:
The pillar at has height 9 and the pillar at has height 12 . Since the solar panel is flat, the inclination from pillar to pillar is 3 . Call the center of the hexagon . Since , it follows that the solar panel has height 13 at . Since the solar panel is flat, the heights of the solar panel at , and are collinear. Therefore, the pillar at has height
Solution 2:
Let the height of the pillar at be . Notice that the difference between the heights of pillar and pillar is equal to the difference between the heights of pillar and pillar . So, the height at is . Now, doing the same thing for pillar we get the height is . Therefore, we can see the difference between the heights at pillar and pillar is half the difference between the heights at and , so The answer is (D) 17 .
A farmer's rectangular field is partitioned into by grid of rectangular sections as shown in the figure. In each section the farmer will plant one crop: corn, wheat, soybeans, or potatoes. The farmer does not want to grow corn and wheat in any two sections that share a border, and the farmer does not want to grow soybeans and potatoes in any two sections that share a border. Given these restrictions, in how many ways can the farmer choose crops to plant in each of the four sections of the field?(2021 AMC Fall 10A, Question #18)
- A.
- B.
- C.
- D.
- E.
Solution 1:
There are possibilities for the top-left section. It follows that the top-right and bottom-left sections each have possibilities, so they have combinations. We have two cases:
1. The top-right and bottom-left sections have the same crop. Note that 3 of the 9 combinations of the top-right and bottom-left sections satisfy this case, from which the bottom-right section has 3 possibilities. Therefore, there are ways in this case.
2. The top-right and bottom-left sections have different crops. Note that 6 of the 9 combinations of the top-right and bottom-left sections satisfy this case, from which the bottom-right section has 2 possibilities. Therefore, there are ways in this case. Together, the answer is (C) 84 .
Solution 2:
We will do casework on the type of crops in the field.
Case 1: all of a kind. If all four sections have the same type of crop, there are simply ways to choose crops for the sections.
Case 2: 3 of a kind, 1 of another kind. Since the one of another kind must be adjacent to two of the other crops, when choosing the type of crops in this case, we cannot choose soybeans and potatoes, or corn and wheat. Therefore, there are choices for the two crops we choose for the section (notice we did not choose by 2 , since the crop we pick first will be the unique one), and 4 ways to choose which section the unique crop is planted on. This gives us a total of ways to choose crops for the sections.
Case 3: of a kind, 2 of another kind. We cannot choose corn and wheat, or soybeans and potatoes, once again, because if we do, the two would have to be adjacent in some way, which the problem disallows. So, there are ways to choose our two crops (notice that we did choose by 2 , since there are two of both crops). There are ways to choose where one of the crops go, so there are ways to choose crops for the sections.
Case 4: 2 of a kind, 1 of another kind, 1 of another kind. In cases 2 and 3, we excluded the possibility of choosing bad pairs for our crops (i.e. soybeans and potatoes, or corn and wheat). In this case, it is inevitable that we choose a bad pair, because we are choosing 3 crops this time. The two sections of the same kind must contain the crop that is not part of the bad pair in the trio: for example, if we choose corn, soybeans and potatoes as our three crop types, nor soybeans and potatoes can be the type which occupies two sections in this case; corn must be the one to do so. There are 4 ways to choose the crop that is not part of the bad pair, and then 1 way to choose the bad pair, giving us ways to choose the crops. To separate the bad pair of crops, the two of a kind must be diagonally placed. There are 2 ways to choose where the two of a kind go, and 2 ways to choose which of the bad pair goes where, giving us ways to choose the positions for the crops. In total, there are ways to choose crops for the sections.
Case 5: every single crop. Bad pairs must be on the same diagonal, so there are 2 ways to choose which pair gets which diagonal, and ways to choose which of each pair goes where on the diagonal, giving us ways to choose crops for the sections. Adding up all our values, we get our final answer of (C) 84 .
A disk of radius 1 rolls all the way around the inside of a square of side length and sweeps out a region of area . A second disk of radius 1 rolls all the way around the outside of the same square and sweeps out a region of area . The value of can be written as , where , and are positive integers and and are relatively prime. What is (2021 AMC Fall 10A, Question #19)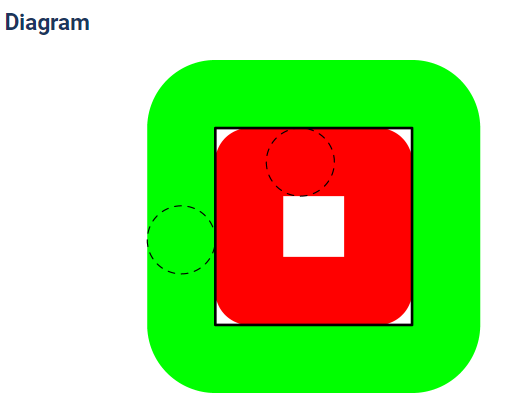
- A.
- B.
- C.
- D.
- E.
The side length of the inner square traced out by the disk with radius 1 is . However, there is a piece at each corner (bounded by two line segments and one arc) where the disk never sweeps out. The combined area of these four pieces is . As a result, we have Now, we consider the second disk. The part it sweeps is comprised of four quarter circles with radius 2 and four rectangles with side lengths of 2 and . When we add it all together, we have , or We equate the expressions for , and then solve for : We get , so the answer is (A) 10 .
How many ordered pairs of positive integers exist where both and do not have distinct, real solutions?(2021 AMC Fall 10A, Question #20)
- A.
- B.
- C.
- D.
- E.
Solution 1:
A quadratic equation does not have real solutions if and only if the discriminant is nonpositive. We conclude that: 1. Since does not have real solutions, we have . 2. Since does not have real solutions, we have . Squaring the first inequality, we get . Multiplying the second inequality by 16 , we get . Combining these results, we get We apply casework to the value of : - If , then , from which . - If , then , from which . - If , then , from which . - If , then , from which . Together, there are ordered pairs , namely , and .
Solution 2:
Similar to Solution 1 , use the discriminant to get and . These can be rearranged to and . Now, we can roughly graph these two inequalities, letting one of them be the axis and the other be . The graph of solutions should be above the parabola and under its inverse, meaning we want points on the graph or in the first area enclosed by the two graphs:
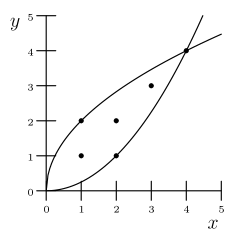
We are looking for lattice points (since and are positive integers), of which we can count (B) 6 .
Each of the 20 balls is tossed independently and at random into one of the 5 bins. Let be the probability that some bin ends up with 3 balls, another with 5 balls, and the other three with 4 balls each. Let be the probability that every bin ends up with 4 balls. What is ?(2021 AMC Fall 10A, Question #21)
- A.
- B.
- C.
- D.
- E.
Solution 1:
For simplicity purposes, we assume that the balls are indistinguishable and the bins are distinguishable. Let be the number of ways to distribute 20 balls into 5 bins. We have Therefore, the answer is Remark By the stars and bars argument, we get
Solution 2:
For simplicity purposes, the balls are indistinguishable and the bins are distinguishable. Let be equal to where is the total number of combinations and is the number of cases where every bin ends up with 4 balls. Notice that we can take 1 ball from one bin and place it in another bin so that some bin ends up with 3 balls, another with 5 balls, and the other three with 4 balls each. We have Therefore, we get , from which
Inside a right circular cone with base radius and height are three congruent spheres with radius . Each sphere is tangent to the other two spheres and also tangent to the base and side of the cone. What is ?(2021 AMC Fall 10A, Question #22)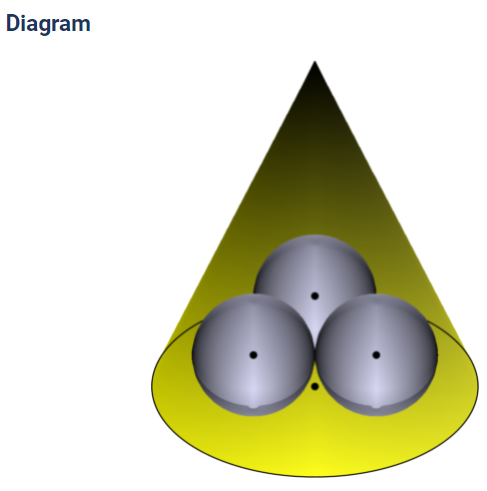
- A.
- B.
- C.
- D.
- E.
Solution 1:
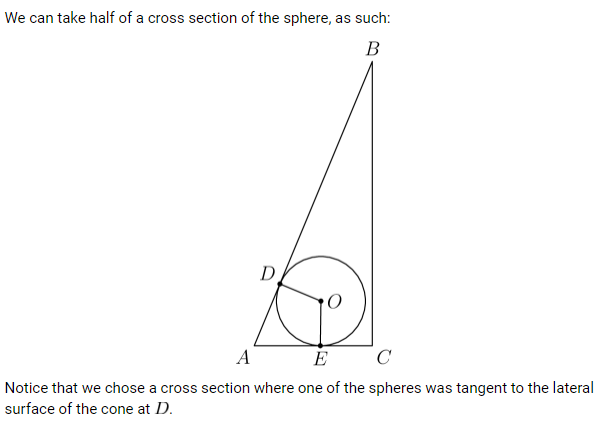
Notice that we chose a cross section where one of the spheres was tangent to the lateral surface of the cone at . To evaluate , we will find and in terms of ; we also know that , so with this, we can solve . Firstly, to find , we can take a bird's eye view of the cone: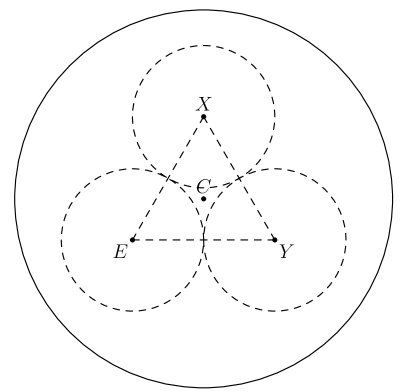
Note that is the centroid of equilateral triangle . Also, since all of the medians of an equilateral triangle are also altitudes, we want to find two-thirds of the altitude from to ; this is because medians cut each other into a to ratio. This equilateral triangle has a side length of , therefore it has an altitude of length ; two thirds of this is , so
To evaluate in terms of , we will extend past point to at point is similar to . Also, is the angle bisector of . Therefore, by the angle bisector theorem, . Also, , so , so . This means that We have that and that , so . We also were given that . Therefore, we have This is a simple linear equation in terms of . We can solve for to get
Solution 2:
We will use coordinates. WLOG, let the coordinates of the center of the base of the cone be the origin. Then, let the center of one of the spheres be . Note that the distance between this point and the plane given by is . Thus, by the point-to-plane distance formula, we have Solving for yields (B)
For each positive integer , let be twice the number of positive integer divisors of , and for , let . For how many values of is ?(2021 AMC Fall 10A, Question #23)
- A.
- B.
- C.
- D.
- E.
Solution 1:
First, we can test values that would make true. For this to happen must have 6 divisors, which means its prime factorization is in the form or , where and are prime numbers. Listing out values less than 50 which have these prime factorizations, we find for , and just 32 for . Here 12 especially catches our eyes, as this means if one of , each of will all be 12 . This is because (as given in the problem statement), so were , plugging this in we get , and thus the pattern repeats. Hence, as long as for a , such that and must be true, which also immediately makes all our previously listed numbers, where , possible values of .
We also know that if were to be any of these numbers, would satisfy as well. Looking through each of the possibilities aside from 12, we see that could only possibly be equal to 20 and 18 , and still have less than or equal to 50 . This would mean must have 10 , or 9 divisors, and testing out, we see that will then be of the form , or . The only two values less than or equal to 50 would be 48 and 36 respectively. From here there are no more possible values, so tallying our possibilities we count (D) 10 values (Namely ).
Solution 2:
Observation 1: . Hence, if has the property that for some , then for all .
Observation 2: . Hence, if has the property that for some , then for all .
Case 1: We have . Hence, Observation 2 implies .
Case 2: is prime. We have . Hence, Observation 2 implies .
Case 3 : The prime factorization of takes the form . We have . Hence, Observation 2 implies .
Case 4 : The prime factorization of takes the form . We have . Hence, Observation 2 implies .
Case 5 : The prime factorization of takes the form . We have . Hence, Observation 2 implies .
Case 6 : The prime factorization of takes the form . We have . Hence, Observation 1 implies . In this case the only is .
Case 7: The prime factorization of takes the form . We have . Hence, Observation 2 implies .
Case 8 : The prime factorization of takes the form . We have . Hence, Observation 1 implies . In this case, all are .
Case 9 : The prime factorization of takes the form . We have . Hence, Observation 2 implies .
Case 10: The prime factorization of takes the form . We have . Hence, Observation 1 implies . In this case, the only is 48 .
Case 11: The prime factorization of takes the form . We have . Hence, Observation 1 implies . In this case, the only is 36 .
Case 12: The prime factorization of takes the form . We have . Hence, Observation 2 implies .
Putting all cases together, the number of feasible $n text { is (D) } 10
Each of the edges of a cube is labeled or . Two labelings are considered different even if one can be obtained from the other by a sequence of one or more rotations and/or reflections. For how many such labelings is the sum of the labels on the edges of each of the faces of the cube equal to ?(2021 AMC Fall 10A, Question #24)
- A.
- B.
- C.
- D.
- E.
Solution 1:
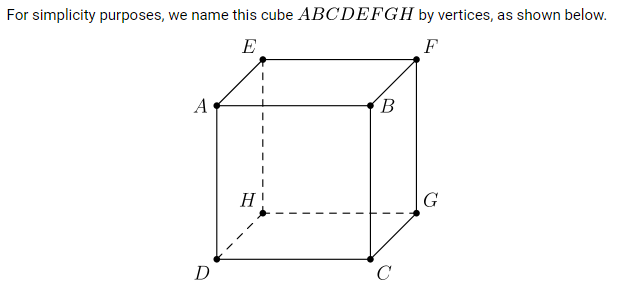
Note that for each face of this cube, two edges are labeled 0 and two edges are labeled 1 . For all twelve edges of this cube, we conclude that six edges are labeled 0 , and six edges are labeled
We apply casework to face . Recall that there are ways to label its edges:
1. Opposite edges have the same label. There are 2 ways to label the edges of . We will consider one of the ways, then multiply the count by 2 . Without the loss of generality, we assume that are labeled , respectively: We apply casework to the label of , as shown below.
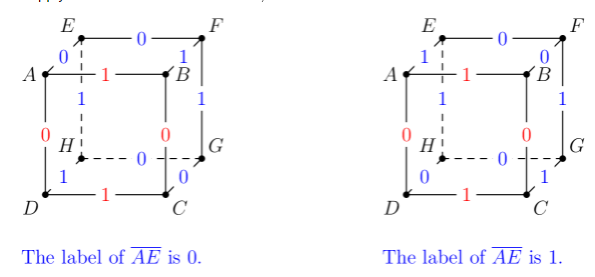
We have such labelings for this case.
2. Opposite edges have different labels. There are 4 ways to label the edges of . We will consider one of the ways, then multiply the count by 4 . Without the loss of generality, we assume that are labeled , respectively: We apply casework to the labels of and , as shown below.
We have such labelings for this case. Therefore, we have (E) 20 such labelings in total.
Solution 2:
Since we want the sum of the edges of each face to be , we need there to be two 1 s and two 0s on each face. Through experimentation, we find that either , or all of them have adjacent to and adjacent to on each face. WLOG, let the first face (counterclockwise) be . In this case we are trying to have all of them be adjacent to each other. First face: . Second face: choices: or . After that, it is basically forced and everything will fall in to place. Since we assumed WLOG, we need to multiply by to get a total of 8 different arrangements.
Secondly, 4 of the faces have all of them adjacent and of the faces do not: WLOG counting counterclockwise, we have . Then, we choose the other face next to it. There are two cases, which are and . Therefore, this subcase has 4 different arrangements. Then, we can choose the face at front to be . This has 4 cases. The sides can either be or . Therefore, we have another 8 cases. Summing these up, we have . Therefore, our answer is . Remark It is very easy to get disorganized when counting, so when doing this problem, make sure to draw a diagram of the cube. Labeling is a bit harder, since we often confuse one side with another. Try doing the problem by labeling sides on the lines (literally letting the lines pass through your and .) I found that to be very helpful when solving this problem.
A quadratic polynomial with real coefficients and leading coefficient 1 is called disrespectful if the equation is satisfied by exactly three real numbers. Among all the disrespectful quadratic polynomials, there is a unique such polynomial for which the sum of the roots is maximized. What is ?(2021 AMC Fall 10A, Question #25)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Let and be the roots of . Then, . The solutions to is the union of the solutions to and Note that one of these two quadratics has one solution (a double root) and the other has two as there are exactly three solutions. WLOG, assume that the quadratic with one root is . Then, the discriminant is 0 , so . Thus, , but for to have two solutions, it must be the case that . It follows that the sum of the roots of is , whose maximum value occurs when . Solving for yields . Therefore, , so (A) . Remark * For to have two solutions, the discriminant must be positive. From here, we get that , so . Hence, is negative, so .
Solution 2:
Let for some real constants and . Suppose that has real roots and . Since , we conclude that or . Without the loss of generality, we assume that has two real solutions and has one real solution. Therefore, we have , from which . As , we expand the left side to obtain , or Since has real solutions for , the discriminant is nonnegative: . We solve this inequality to get . Either by the axis of symmetry or Vieta's Formulas, note that . As we wish to maximize , we maximize . Substituting into , we obtain . We factor the left side to get , or . Finally, the unique such polynomial is from which (A)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
