2021 AMC 10 B Fall
Complete problem set with solutions and individual problem pages
What is the value of (2021 AMC Fall 10B, Question #1)
- A.
- B.
- C.
- D.
- E.
Solution 1:
We see that , and 4 each appear in the ones, tens, hundreds, and thousands digit exactly once. Since , we find that the sum is equal to Note that it is equally valid to manually add all four numbers together to get the answer.
Solution 2:
We have
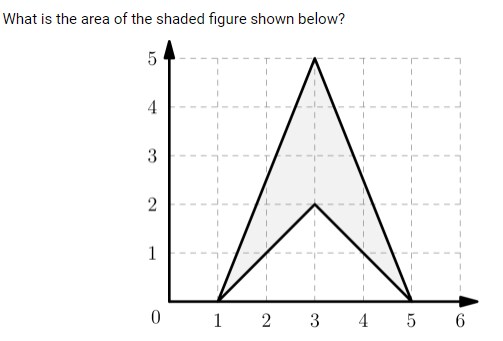 (2021 AMC Fall 10B, Question #2)
(2021 AMC Fall 10B, Question #2)
- A.
- B.
- C.
- D.
- E.
Solution 1:
The line of symmetry divides the shaded figure into two congruent triangles, each with base 3 and height 2 . Therefore, the area of the shaded figure is
Solution 2:
To find the area of the shaded figure, we subtract the area of the smaller triangle (base 4 and height 2 ) from the area of the larger triangle (base 4 and height 5 ):
The expression is equal to the fraction in which and are positive integers whose greatest common divisor is 1 . What is ?(2021 AMC Fall 10B, Question #3)
- A.
- B.
- C.
- D.
- E.
Solution 1:
We write the given expression as a single fraction: by cross multiplication. Then by factoring the numerator, we get The question is asking for the numerator, so our answer is , giving answer choice (E).
Solution 2:
Denote . Hence, We observe that and . Hence, . Therefore, . Therefore, the answer is (E) 4041
At noon on a certain day, Minneapolis is degrees warmer than St. Louis. At the temperature in Minneapolis has fallen by degrees while the temperature in St. Louis has risen by degrees, at which time the temperatures in the two cities differ by degrees. What is the product of all possible values of ?(2021 AMC Fall 10B, Question #4)
- A.
- B.
- C.
- D.
- E.
Solution 1:
At noon on a certain day, let and be the temperatures (in degrees) in Minneapolis and St. Louis, respectively. It follows that . At , we get We have two cases: 1. If , then . 2. If , then . Together, the product of all possible values of is .
Solution 2:
At noon on a certain day, the difference of temperatures in Minneapolis and St. Louis is degrees.
At , the difference of temperatures in Minneapolis and St. Louis is degrees. It follows that We continue with the casework in Solution 1 to get the answer .
Let . Which of the following is equal to ?(2021 AMC Fall 10B, Question #5)
- A.
- B.
- C.
- D.
- E.
Solution 1:
We have Therefore,
Solution 2:
The requested value is
The least positive integer with exactly distinct positive divisors can be written in the form , where and are integers and is not a divisor of . What is (2021 AMC Fall 10B, Question #6)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Let this positive integer be written as . The number of factors of this number is therefore , and this must equal 2021. The prime factorization of 2021 is , so and . To minimize this integer, we set and . Then this integer is . Now and so
Solution 2:
Recall that can be written as . Since we want the integer to have 2021 divisors, we must have it in the form , where and are prime numbers. Therefore, we want to be 3 and to be 2 . To make up the remaining , we multiply by , which is which is 16 . Therefore, we have
Call a fraction , not necessarily in the simplest form, special if and are positive integers whose sum is . How many distinct integers can be written as the sum of two, not necessarily different, special fractions?(2021 AMC Fall 10B, Question #7)
- A.
- B.
- C.
- D.
- E.
Solution 1:
The special fractions are We rewrite them in the simplest form: Note that two unlike fractions in the simplest form cannot sum to an integer. So, we only consider the fractions whose denominators appear more than once: For the set , two elements (not necessarily different) can sum to . For the set , two elements (not necessarily different) can sum to .
For the set , two elements (not necessarily different) can sum to 3 . Together, there are (C) 11 distinct integers that can be written as the sum of two, not necessarily different, special fractions:
Solution 2:
Let , so the special fraction is We can ignore the part and only focus on . The integers are , which are , respectively. We get from this group of numbers.
The halves are , which are , respectively. We get from this group of numbers. The quarters are , which are , respectively. We get 5 from this group of numbers. Note that 10 and 5 each appear twice. Therefore, the answer is (C) 11 .
The largest prime factor of is because . What is the sum of the digits of the greatest prime number that is a divisor of ?(2021 AMC Fall 10B, Question #8)
- A.
- B.
- C.
- D.
- E.
We have Therefore, the greatest prime divisor of 16383 is 127 . The sum of its digits is .
The knights in a certain kingdom come in two colors. of them are red, and the rest are blue. Furthermore, of the knights are magical, and the fraction of red knights who are magical is times the fraction of blue knights who are magical. What fraction of red knights are magical?(2021 AMC Fall 10B, Question #9)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Let be the number of knights: then the number of red knights is and the number of blue knights is . Let be the fraction of blue knights that are magical - then is the fraction of red knights that are magical. Thus we can write the equation We want to find the fraction of red knights that are magical, which is
Solution 2:
We denote by the fraction of red knights who are magical. Hence, By solving this equation, we get . Therefore, the answer is (C) .
Forty slips of paper numbered to are placed in a hat. Alice and Bob each draw one number from the hat without replacement, keeping their numbers hidden from each other. Alice says, "I can't tell who has the larger number." Then Bob says, "I know who has the larger number." Alice says, "You do? Is your number prime?" Bob replies, "Yes." Alice says, "In that case, if I multiply your number by 100 and add my number, the result is a perfect square. " What is the sum of the two numbers drawn from the hat?(2021 AMC Fall 10B, Question #10)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Because Alice doesn't know who has the larger number, she doesn't have 1 . Because Alice says that she doesn't know who has the larger number, Bob knows that she doesn't have 1 . But Bob knows who has the larger number, this implies that Bob has the smallest possible number. Because Bob's number is prime, Bob's number is 2 . Thus, the perfect square is in the . The only perfect square is 225 . Thus, Alice's number is 25 . The sum of Alice's and Bob's number is . Thus the answer is .
Solution 2:
Denote by and the numbers drawn by Alice and Bob, respectively. Alice's sentence " 1 can't tell who has the larger number. implies . Bob's sentence "I know who has the larger number. implies . Their subsequent conversation that is prime implies . Then, Alice's next sentence "In that case, if I multiply your number by 100 and add my number, the result is a perfect square. implies is a perfect square. Hence, . Therefore, the answer is (A) 27 .
A regular hexagon of side length is inscribed in a circle. Each minor arc of the circle determined by a side of the hexagon is reflected over that side. What is the area of the region bounded by these 6 reflected arcs?(2021 AMC Fall 10B, Question #11)
- A.
- B.
- C.
- D.
- E.
Solution 1:

This is the graph of the original Hexagon. After reflecting each minor arc over the sides of the hexagon it will look like this;
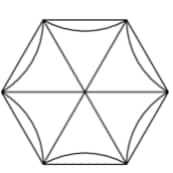
This bounded region is the same as the area of the hexagon minus the area of each of the reflect arcs. From the first diagram, the area of each arc is the area of the sector minus the area of the equilateral triangle, so each arc has an area of . There are 6 total arcs, so the total area of the arcs is . The area of the hexagon is , so the area of the bounded region is:
Solution 2:
Let the hexagon described be of area and let the circle's area be . Let the area we want to aim for be . Thus, we have that , or . By some formulas, and . Thus, or .
Which of the following conditions is sufficient to guarantee that integers , and satisfy the equation (2021 AMC Fall 10B, Question #12)
- A.
and
- B.
and
- C.
and
- D.
and
- E.
Solution 1:
It is obvious , and are symmetrical. We are going to solve the problem by Completing the Square. Because are integers, , and can only equal . So one variable must equal another, and the third variable is 1 different from those 2 equal variables. So the answer is .
Solution 2:
Plugging in every choice, we see that choice (D) works. We have , so Our answer is (D).
A square with side length is inscribed in an isosceles triangle with one side of the square along the base of the triangle. A square with side length has two vertices on the other square and the other two on sides of the triangle, as shown. What is the area of the triangle?(2021 AMC Fall 10B, Question #13)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Let's split the triangle down the middle and label it:
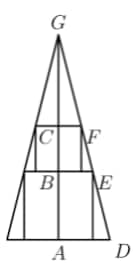
We see that by AA similarity. because cuts the side length of the square in half; similarly, . Let : then by side ratios, Now the height of the triangle is . By side ratios, The area of the triangle is
Solution 2:
By similarity, the height is and the base is . Thus the area is , or
Una rolls standard -sided dice simultaneously and calculates the product of the 6 numbers obtained. What is the probability that the product is divisible by ?(2021 AMC Fall 10B, Question #14)
- A.
- B.
- C.
- D.
- E.
We will use complementary counting to find the probability that the product is not divisible by . Then, we can find the probability that we want by subtracting this from . We split this into cases.
Case 1: The product is not divisible by We need every number to be odd, and since the chance we roll an odd number is , our probability is .
Case 2 : The product is divisible by , but not by . We need 5 numbers to be odd, and one to be divisible by 2 , but not by . There is a chance that an odd number is rolled, a chance that we roll a number satisfying the second condition (only 2 and 6 work), and 6 ways to choose the order in which the even number appears. Our probability is . Therefore, the probability the product is not divisible by is . Our answer is (C)
In square , points and lie on and , respectively. Segments and intersect at right angles at , with and . What is the area of the square?(2021 AMC Fall 10B, Question #15)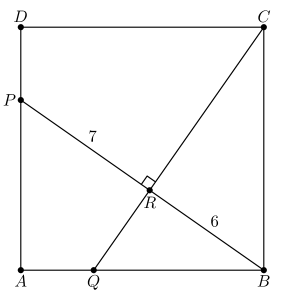
- A.
- B.
- C.
- D.
- E.
Solution 1:
Note that . Then, it follows that . Thus, . Define to be the length of side , then . Because is the altitude of the triangle, we can use the property that . Substituting the given lengths, we have Solving, gives and . We eliminate the possibilty of because . Thus, the side length of the square, by Pythagorean Theorem, is Thus, the area of the sqaure is . Thus, the answer is (D) 117
Solution 2:
As above, note that , which means that . In addition, note that is the altitude of a right triangle to its hypotenuse, so . Let the side length of the square be ; using similarity side ratios of to , we get Note that by the Pythagorean theorem, so we can use the expansion to produce two equations and two variables; We want , so we want to find . Subtracting the first equation from the second, we get Then
Five balls are arranged around a circle. Chris chooses two adjacent balls at random and interchanges them. Then Silva does the same, with her choice of adjacent balls to interchange being independent of Chris's. What is the expected number of balls that occupy their original positions after these two successive transpositions?(2021 AMC Fall 10B, Question #16)
- A.
- B.
- C.
- D.
- E.
After the first swap, we do casework on the next swap.
Case 1: Silva swaps the two balls that were just swapped There is only one way for Silva to do this, and it leaves 5 balls occupying their original position.
Case 2: Silva swaps one ball that has just been swapped with one that hasn't swapped There are two ways for Silva to do this, and it leaves balls occupying their original positions.
Case 3 : Silva swaps two balls that have not been swapped There are two ways for Silva to do this, and it leaves balls occupying their original positions. Our answer is the average of all 5 possible swaps, so we get
Distinct lines and lie in the -plane. They intersect at the origin. Point is reflected about line to point , and then is reflected about line to point . The equation of line is , and the coordinates of are . What is the equation of line ?(2021 AMC Fall 10B, Question #17)
- A.
- B.
- C.
- D.
- E.
Solution 1:
It is well known that the composition of 2 reflections, one after another, about two lines and , respectively, that meet at an angle is a rotation by around the intersection of and . Now, we note that is a 90 degree rotation clockwise of about the origin, which is also where and intersect. So is a 45 degree rotation of about the origin clockwise. To rotate degrees clockwise, we build a square with adjacent vertices and . The other two vertices are at and . The center of the square is at , which is the midpoint of and . The line passes through the origin and the center of the square we built, namely at and . Thus the line is . The answer is (D) .
Solution 2:
We know that the equation of line is . This means that is reflected over the line . This means that the line with and is perpendicular to , so it has slope . Then the equation of this perpendicular line is , and plugging in for and yields .
The midpoint of and lies at the intersection of and . Solving, we get the -value of the intersection is and the -value is . Let the x-value of be then by the midpoint formula, . We can find the -value of the same way, so .
Now we have to reflect over to get to . The midpoint of and will lie on , and this midpoint is, by the midpoint formula, must satisfy this point, so Now the equation of line is
Three identical square sheets of paper each with side length 6 are stacked on top of each other. The middle sheet is rotated clockwise about its center and the top sheet is rotated clockwise about its center, resulting in the -sided polygon shown in the figure below. The area of this polygon can be expressed in the form , where , and are positive integers, and is not divisible by the square of any prime. What is ?(2021 AMC Fall 10B, Question #18)
- A.
- B.
- C.
- D.
- E.
Solution 1:
First note the useful fact that if is the circumradius of a dodecagon (12-gon) the area of the figure is . If we connect the vertices of the 3 squares we get a dodecagon. The radius of circumcircle of the dodecagon is simply half the diagonal of the square, which is . Thus the area of the dodecagon is . But, the problem asks for the area of figure of rotated squares. This area is the area of the dodecagon, which was found, subtracting the 12 isosceles triangles, which are formed when connecting the vertices of the squares to created the dodecagon. To find this area, we need to know the base of the isosceles triangle, call this . Then, we can use Law of Cosines, on the triangle that is formed from the two vertices of the square and the center of the square. After computing, we get that . Realize that the 12 isosceles are congruent with an angle measure of , this means that we can create 4 congruent equilateral triangles with side length of . The area of the equilateral triangle is . Thus, the area of all the twelve small equilateral traingles are . Thus, the requested area is . Thus, . Thus, the answer is (E)147.
Solution 2:
As shown in Image:2021_AMC_12B_(Nov)_Problem_15,_sol.png,
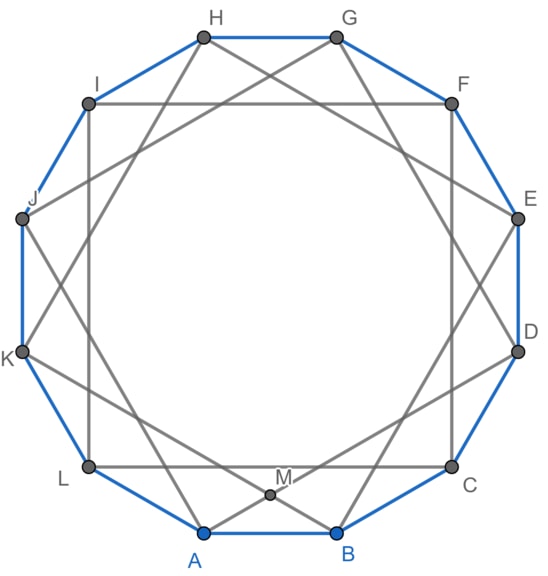
all 12 vertices of three squares form a regular dodecagon (12-gon). Denote by the center of this dodecagon. Hence, . Because the length of a side of a square is . Hence, . We notice that . Hence, . Therefore, the area of the region that three squares cover is Therefore, the answer is (E) 147 .
Let be the positive integer , a -digit number where each digit is a . Let be the leading digit of the th root of . What is (2021 AMC Fall 10B, Question #19)
- A.
- B.
- C.
- D.
- E.
Solution 1:
We can rewrite as . When approximating values, as we will shortly do, the minus one will become negligible so we can ignore it. When we take the power of ten out of the square root, we'll be multiplying by another power of ten, so the leading digit will not change. Thus the leading digit of will be equal to the leading digit Then is the first digit of The final answer is therefore
Solution 2:
For notation purposes, let be the number with 313 digits, and let be the leading digit of . As an example, , because , and the first digit of that is 7 . Notice that for all numbers ; this is because , and dividing by 10 does not affect the leading digit of a number. Similarly, In general, for positive integers and real numbers , it is true that Behind all this complex notation, all that we're really saying is that the first digit of something like has the same first digit as and . The problem asks for From our previous observation, we know that Therefore, . We can evaluate , the leading digit of , to be 2 . Therefore, . Similarly, we have Therefore, . We know , so .
Next, and , so . We also have and , so . Finally, and , so . We have that (A) 8 .
In a particular game, each of players rolls a standard -sided die. The winner is the player who rolls the highest number. If there is a tie for the highest roll, those involved in the tie will roll again and this process will continue until one player wins. Hugo is one of the players in this game. What is the probability that Hugo's first roll was a , given that he won the game?(2021 AMC Fall 10B, Question #20)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Since we know that Hugo wins, we know that he rolled the highest number in the first round. The probability that his first roll is a 5 is just the probability that the highest roll in the first round is 5 . Let indicate the probability that event occurs. We find that No one rolls a 6 No one rolls a 5 or 6 The highest roll is a 5, so The highest roll is a 5.
Solution 2:
The conditional probability formula states that , where means given and means and . Therefore the probability that Hugo rolls a five given he won is , where is the probability that he rolls a five and is the probability that he wins. In written form, The probability that Hugo wins is by symmetry since there are four people playing and there is no bias for any one player. The probability that he gets a and wins is more difficult; we will have to consider cases on how many players tie with Hugo\cdots
Case 1: No Players Tie In this case, all other players must have numbers from 1 through four. There is a chance of this happening.
Case 2: One Player Ties In this case, there are ways to choose which other player ties with Hugo, and the probability that this happens is . The probability that Hugo wins on his next round is then because there are now two players rolling die. Therefore the total probability in this case is .
Case 3: Two Players Tie In this case, there are ways to choose which other players tie with Hugo, and the probability that this happens is . The probability that Hugo wins on his next round is then because there are now three players rolling the die. Therefore the total probability in this case is .
Case 4: All Three Players Tie In this case, the probability that all three players tie with Hugo is . The probability that Hugo wins on the next round is , so the total probability is . Finally, Hugo has a probability of rolling a five himself, so the total probability is Finally, the total probability is this probability divided by which is this probability times four; the final answer is
Regular polygons with , and sides are inscribed in the same circle. No two of the polygons share a vertex, and no three of their sides intersect at a common point. At how many points inside the circle do two of their sides intersect?(2021 AMC Fall 10B, Question #21)
- A.
- B.
- C.
- D.
- E.
Imagine we have regular polygons with and sides and inscribed in a circle without sharing a vertex. We see that each side of the polygon with sides (the polygon with fewer sides) will be intersected twice. (We can see this because to have a vertex of the mgon on an arc subtended by a side of the n-gon, there will be one intersection to "enter" the arc and one to "exit" the arc. KingRavi)
This means that we will end up with times the number of sides in the polygon with fewer sides.
If we have polygons with , and sides, we need to consider each possible pair of polygons and count their intersections. Throughout 6 of these pairs, the -sided polygon has the least number of sides times, the 6 sided polygon has the least number of sides times, and the -sided polygon has the least number of sides 1 time. Therefore the number of intersections is .
For each integer , let be the sum of all products , where and are integers and . What is the sum of the 10 least values of such that is divisible by 3 ?(2021 AMC Fall 10B, Question #22)
- A.
- B.
- C.
- D.
- E.
Solution 1:
To get from to , we add Now, we can look at the different values of . For and , then we have . However, for , we have Clearly, . Using the above result, we have , and , and are all divisible by 3 . After , we have , and all divisible by 3 , as well as , and . Thus, our answer is
Solution 2:
Since we have a wonky function, we start by trying out some small cases and see what happens. If is 1 and is 2 , then there is once case. We have for this case. If is 3 , we have which is still . If is 4 , we have to add which is a multiple of 3 , meaning that we are still at 2 mod 3 . If we try a few more cases, we find that when is 8 , we get a multiple of 3 . When is 9 , we are adding , and therefore, we are still at a multiple of 3 .
When is 10 , then we get which is 10 times a multiple of 3 . Therefore, we have another multiple of 3 . When is 11 , so we have 2 mod 3 . So, every time we have , and , we always have a multiple of 3 . Think about it: When is 1 , it will have to be , so it is a multiple of 3 . Therefore, our numbers are . Adding the numbers up, we get (B) 197
Each of the sides and the diagonals of a regular pentagon are randomly and independently colored red or blue with equal probability. What is the probability that there will be a triangle whose vertices are among the vertices of the pentagon such that all of its sides have the same color?(2021 AMC Fall 10B, Question #23)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Instead of finding the probability of a same-colored triangle appearing, let us find the probability that one does not appear. After drawing the regular pentagon out, note the topmost vertex; it has 4 sides/diagonals emanating outward from it. We do casework on the color distribution of these sides/diagonals.
Case 1: all 4 are colored one color. In that case, all of the remaining sides must be of the other color to not have a triangle where all three sides are of the same color. We can correspondingly fill out each color based on this constraint, but in this case you will always end up with a triangle where all three sides have the same color by inspection.
Case 2: are one color and one is the other. Following the steps from the previous case, you can try filling out the colors, but will always arrive at a contradiction so this case does not work either.
Case 3: are one color and 2 are of the other color. Using the same logic as previously, we can color the pentagon 2 different ways by inspection to satisfy the requirements. There are ways to color the original sides/diagonals and 2 ways after that to color the remaining ones for a total of ways to color the pentagon so that no such triangle has the same color for all of its sides. These are all the cases, and there are a total of ways to color the pentagon. Therefore the answer is
Solution 2:
This problem is related to a special case of Ramsey's Theorem, . Suppose we color every edge of a vertex complete graph with 2 colors, there must exist a vertex complete graph with all it's edges in the same color. That is, with edges in colors contains a monochromatic . For with edges in colors, a monochromatic does not always exist.
This is a problem about the probability of a monochromatic exist in a 5 vertex complete graph with edges in colors. Choose a vertex, it has edges.
Case 1: When 3 or more edges are the same color, there must exist a monochromatic . Suppose the color is red, as shown below.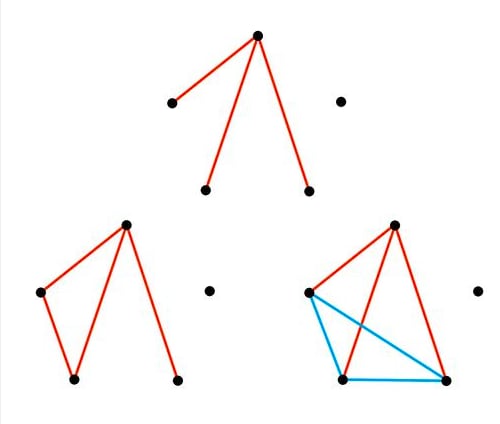 There is only 1 way to color all the edges in the same color. There is ways to color 3 edges in the same color. There are 2 colors. The probability of 3 or more edges the same color is . So the probability of containing a monochromatic is .
There is only 1 way to color all the edges in the same color. There is ways to color 3 edges in the same color. There are 2 colors. The probability of 3 or more edges the same color is . So the probability of containing a monochromatic is .
Case 2: When 2 edges are the same color, graphs that does not contain a monochromatic can exist. The following diagram shows steps to obtain graphs that does not contain a monochromatic .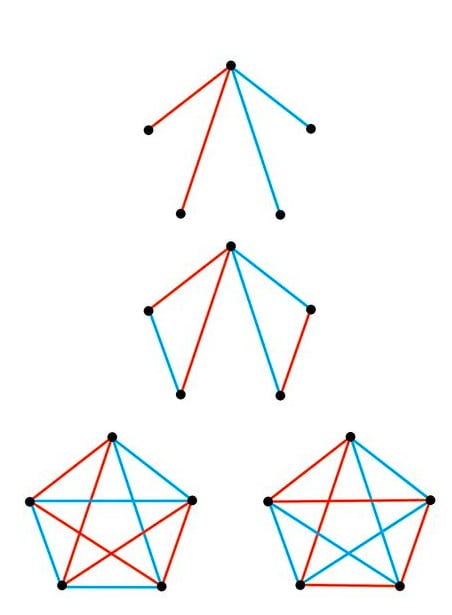
There are ways to choose 2 edges with the same color. For the other 4 vertices there are edges among them, there are ways to color the edges. There are only 2 cases without a monochromatic . So the probability without monochromatic is .
The probability with monochromatic is . From case 1 and case 2 , the probability with monochromatic is D)
A cube is constructed from white unit cubes and blue unit cubes. How many different ways are there to construct the cube using these smaller cubes? (Two constructions are considered the same if one can be rotated to match the other.)(2021 AMC Fall 10B, Question #24)
- A.
- B.
- C.
- D.
- E.
Solution 1:
This problem is about the relationships between the white unit cubes and the blue unit cubes, which can be solved by Graph Theory. We use a Planar Graph to represent the larger cube. Each vertex of the planar graph represents a unit cube. Each edge of the planar graph represents a shared face between neighboring unit cubes. Each face of the planar graph represents a face of the larger cube. Now the problem becomes a Graph Coloring problem of how many ways to assign vertices blue and vertices white with Topological Equivalence. For example, in Figure (1), as long as the blue vertices belong to the same planar graph face, the different planar graphs are considered to be topological equivalent by rotating the larger cube.

Here is how the 4 blue unit cubes are arranged: In Figure (1): 4 blue unit cubes are on the same layer (horizontal or vertical). In Figure (2): 4 blue unit cubes are in shape. In Figure (3) and (4): 4 blue unit cubes are in shape. In Figure (5): 3 blue unit cubes are in shape, and the other is isolated without a shared face.
In Figure (6): 2 pairs of neighboring blue unit cubes are isolated from each other without a shared face. In Figure ( 7 blue unit cubes are isolated from each other without a shared face. So the answer is (A) 7
Solution 2:
Let's split the cube into two layers; a bottom and top. Note that there must be four of each color, so however many number of one color are in the bottom, there will be four minus that number of the color on the top. We do casework on the color distribution of the bottom layer.
Case 1: In this case, there is only one possibility for the top layer - all of the other color - . Therefore there is 1 construction from this case.
Case 2: In this case, the top layer has four possibilities, because there are four different ways to arrange it so that it also has a 3, 1 color distribution - . Therefore there are 4 constructions from this case.
Case 3: In this case, the top layer has six possibilities of arrangement - . However, having adjacent colors one way can be rotated to having adjacent colors any other way, so there is only one construction for the adjacent colors subcase and similarly, only one for the diagonal color subcase. Therefore the total number of constructions for this case is . The total number of constructions for the cube is thus
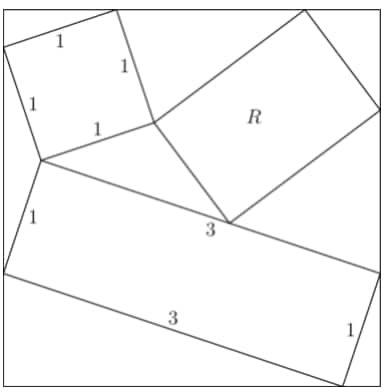
A rectangle with side lengths and , a square with side length , and a rectangle are inscribed inside a larger square as shown. The sum of all possible values for the area of can be written in the form , where and are relatively prime positive integers. What is (2021 AMC Fall 10B, Question #25)
- A.
- B.
- C.
- D.
- E.
Solution 1:
We see that the polygon bounded by the small square, large square, and rectangle of known lengths is an isosceles triangle. Let's draw a perpendicular from the vertex of this triangle to its opposing side;
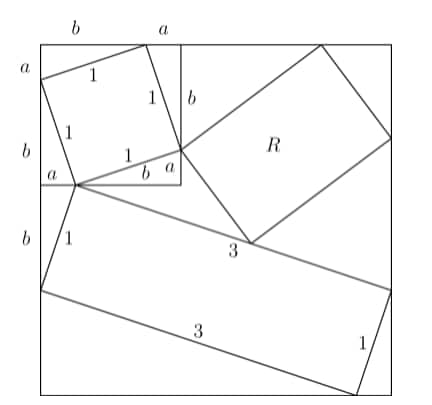
We see that this creates two congruent triangles. Let the smaller side of the triangle have length and let the larger side of the triangle have length . Now we see by AAS congruency that if we draw perpendiculars that surround the smaller square, each outer triangle will be congruent to these two triangles.
Now notice that these small triangles are also similar to the large triangle bounded by the bigger square and the rectangle by AA, and the ratio of the sides are , so we can fill in the lengths of that triangle. Similarly, the small triangle on the right bounded by the rectangle and the square is also congruent to the other small triangles by AAS, so we can fill in those sides;

Since the larger square by definition has all equal sides, we can set the sum of the lengths of the sides equal to each other. . Now let's draw some more perpendiculars and rename the side lengths.
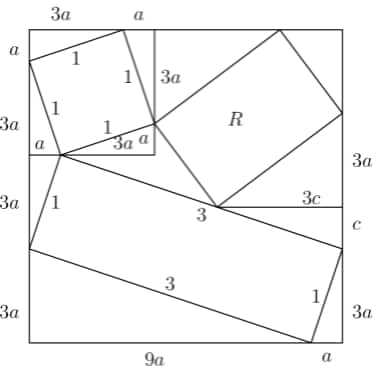
By AA similarity, when we draw a perpendicular from the intersection of the two rectangles to the large square, we create a triangle below that is similar to the small congruent triangles with length . Since we don't know it's scale, we'll label it's sides . The triangle that is created above the perpendicular is congruent to the triangle on the opposite of the rectangle with unknown dimensions because they share the same hypotenuse and have two angles in common. Thus we can label these two triangles accordingly. The side length of the big square is , so we can find the remaining dimensions of the triangle bounded by the rectangle with unknown dimensions and the large square in terms of and :
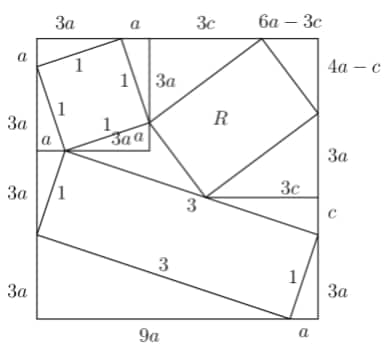
This triangle with side lengths and is similar to the triangle directly below it with side lengths and by AA similarity, so we can set up a ratio equation: There are two solutions to this equation; and . For the first solution, the triangle in the corner has sides and . Using Pythagorean theorem on that triangle, the hypotenuse has length . The triangle directly below has side lengths and in this case, so special right triangle yields the hypotenuse to be . The area of the rectangle is thus . For the second solution, the side lengths of the corner triangle are and , so the hypotenuse of the triangle is . The triangle below that also has side lengths and , so it's hypotenuse is the same. Then the area of the rectangle is The sum of the possible areas of the rectangle is therefore . Using Pythagorean theorem on the original small congruent triangles, or . Therefore the sum of the possible areas of the rectangle is . Therefore , and
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
