2020 AMC 10 A
Complete problem set with solutions and individual problem pages
What value of satisfies ?
- A.
- B.
- C.
- D.
- E.
Adding to both sides, .
The numbers , and have an average (arithmetic mean) of . What is the average of and ?
- A.
- B.
- C.
- D.
- E.
The arithmetic mean of the numbers , and is equal to . Solving for , we get . Dividing by 2 to find the average of the two numbers and gives .
Assuming , and , what is the value in simplest form of the following expression?
(2020 AMC 10A Problems, Question #3)
- A.
- B.
- C.
- D.
- E.
Note that is times . Likewise, is times and is times . Therefore, the product of the given fraction equals
A driver travels for hours at miles per hour, during which her car gets miles per gallon of gasoline. She is paid per mile, and her only expense is gasoline at per gallon. What is her net rate of pay, in dollars per hour, after this expense?
- A.
- B.
- C.
- D.
- E.
Since the driver travels miles per hour and each hour she uses gallons of gasoline, she spends per hour on gas. If she gets per mile, then she gets per hour of driving. Subtracting the gas cost, her net rate of pay per hour is (E) 26
What is the sum of all real numbers for which ?
- A.
- B.
- C.
- D.
- E.
Solution 1 :
Split the equation into two cases, where the value inside the absolute value is positive and nonpositive. Case 1: The equation yields , which is equal to . Therefore, the two values for the positive case is 4 and 8 . Case 2: Similarly, taking the nonpositive case for the value inside the absolute value notation yields . Factoring and simplifying gives , so the only value for this case is 6 . Summing all the values results in
Solution 2:
We have the equations and . Notice that the second is a perfect square with a double root at , and the first has real roots. By Vieta's, the sum of the roots of the first equation is (C) 18
How many 4 -digit positive integers (that is, integers between and , inclusive) having only even digits are divisible by ?
- A.
- B.
- C.
- D.
- E.
The ones digit, for all numbers divisible by , must be either or . However, from the restriction in the problem, it must be even, giving us exactly one choice (0) for this digit. For the middle two digits, we may choose any even integer from , meaning that we have total options. For the first digit, we follow similar intuition but realize that it cannot be , hence giving us possibilities. Therefore, using the multiplication rule, we get .
The integers from to , inclusive, can be arranged to form a by square in which the sum of the numbers in each row, the sum of the numbers in each column, and the sum of the numbers along each of the main diagonals are all the same. What is the value of this common sum?
- A.
- B.
- C.
- D.
- E.
Solution 1:
Without loss of generality, consider the five rows in the square. Each row must have the same sum of numbers, meaning that the sum of all the numbers in the square divided by is the total value per row. The sum of the integers is , and the common sum is .
Solution 2:
Take the sum of the middle values of the set (they will turn out to be the mean of each row). We get as our answer.
What is the value of ?
- A.
- B.
- C.
- D.
- E.
Solution 1: Split the even numbers and the odd numbers apart. If we group every even numbers together and add them, we get a total of . Summing the odd numbers is equivalent to summing the first 100 odd numbers, which is equal to . Adding these two, we obtain the answer of (B) 9900
Solution 2 (bashy): We can break this entire sum down into integer bits, in which the sum is , where is the first integer in this bit. We can find that the first sum of every sequence is , which we plug in for the 50 bits in the entire sequence is , so then we can plug it into the first term of every sequence equation we got above , and so the sum of every bit is , and we only found the value of , the sum of the sequence
A single bench section at a school event can hold either adults or children. When bench sections are connected end to end, an equal number of adults and children seated together will occupy all the bench space. What is the least possible positive integer value of ?
- A.
- B.
- C.
- D.
- E.
Solution 1: The least common multiple of and is . Therefore, there must be adults and children. The total number of benches
Solution 2: This is similar to Solution 1, with the same basic idea, but we don't need to calculate the LCM. Since both and are prime, their LCM must be their product. So the answer would be .
Seven cubes, whose volumes are , and cubic units, are stacked vertically to form a tower in which the volumes of the cubes decrease from bottom to top. Except for the bottom cube, the bottom face of each cube lies completely on top of the cube below it. What is the total surface area of the tower (including the bottom) in square units?
- A.
- B.
- C.
- D.
- E.
Solution 1: The volume of each cube follows the pattern of ascending, for is between and . We see that the total surface area can be comprised of three parts: the sides of the cubes, the tops of the cubes, and the bottom of the cube (which is just ). The sides areas can be measured as the , giving us 560 . Structurally, if we examine the tower from the sum top, we see that it really just forms a square of area 49 . Therefore, we can say that the total surface area is Alternatively, for the area of the tops, we could have found the , giving us as well.
Solution 2: It can quickly be seen that the side lengths of the cubes are the integers from to , inclusive.
First, we will calculate the total surface area of the cubes, ignoring overlap. This value is . Then, we need to subtract out the overlapped parts of the cubes. Between each consecutive pair of cubes, one of the smaller cube's faces is completely covered, along with an equal area of one of the larger cube's faces. The total area of the . Subtracting the overlapped surface area from the total surface area, we
What is the median of the following list of numbers?
- A.
- B.
- C.
- D.
- E.
Solution 1: We can see that is less than . Therefore, there are of the numbers after . Also, there are numbers that are under and equal to . Since is equal to , it, with the other squares, will shift our median's placement up 44 . We can find that the median of the whole set is , and gives us . Our answer (C)
Solution 2: We want to know the th term and the th term to get the median. We know that So numbers are in between to . So the sum of and will result in , which means that is the th number. Also, notice that , which is larger than . Then the th term will be , and similarly the th term will be . Solving for the median of the two numbers, we get (C)
Triangle is isoceles with . Medians and are perpendicular to each other, and . What is the area of
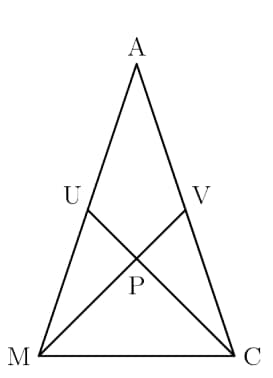
- A.
- B.
- C.
- D.
- E.
Solution 1:
Since quadrilateral has perpendicular diagonals, its area can be found as half of the product of the length of the diagonals. Also note that has the area of triangle by similarity, so
Solution 2:
Connect the line segment and it's easy to see quadrilateral has an area of the product of its diagonals divided by which is . Now, solving for triangle AUV could be an option, but the drawing shows the area of will be less than the quadrilateral meaning the the area of is less than but greater than , leaving only one possible answer choice,C.
A frog sitting at the point begins a sequence of jumps, where each jump is parallel to one of the coordinate axes and has length , and the direction of each jump (up, down, right, or left) is chosen independently at random. The sequence ends when the frog reaches a side of the square with vertices , and . What is the probability that the sequence of jumps ends on a vertical side of the square?
- A.
- B.
- C.
- D.
- E.
Solution 1: Drawing out the square, it's easy to see that if the frog goes to the left, it will immediately hit a vertical end of the square. Therefore, the probability of this happening is . If the frog goes to the right, it will be in the center of the square at , and by symmetry (since the frog is equidistant from all sides of the square), the chance it will hit a vertical side of a square is . The probability of this happening is If the frog goes either up or down, it will hit a line of symmetry along the corner it is closest to and furthest to, and again, is equidistant relating to the two closer sides and also equidistant relating the two further sides. The probability for it to hit a vertical wall is . Because there's a chance of the frog going up and down, the total probability for this case is and summing up all the down, the total probability for this case is cases, (B)
Solution 2: If the frog is on one of the diagonals, the chance of landing on vertical or horizontal each becomes . Since it starts on , there is a chance (up, down, or right) it will reach a diagonal on the first jump and chance (left) it will reach the vertical side. The probablity of landing on a vertical
Real numbers and satisfy and . What is the value of ?
- A.
- B.
- C.
- D.
- E.
Solution 1: Continuing to combine From the givens, it can be concluded that . Also, that . Substituting this information into , we have .
Solution 2: As above, we need to calculate . Note that , are the roots of and so and . Thus where and as in the previous solution. Thus the
A positive integer divisor of is chosen at random. The probability that the divisor chosen is a perfect square can be expressed as , where and are relatively prime positive integers. What is ?
- A.
- B.
- C.
- D.
- E.
The prime factorization of is . This yields a total of divisors of . In order to produce a perfect square divisor, there must be an even exponent for each number in the prime factorization. Note that and can not be in the prime factorization of a perfect square because there is only one of each in . Thus, there are perfect squares. (For , you can have , or , etc.) The probability that the divisor chosen is a perfect square is
A point is chosen at random within the square in the coordinate plane whose vertices are , and . The probability that the point is within units of a lattice point is . (A point is a lattice point if and are both integers.) What is to the nearest tenth?
- A.
- B.
- C.
- D.
- E.
Solution 1: We consider an individual one-by-one block. If we draw a quarter of a circle from each corner (where the lattice points are located), each with radius , the area covered by the circles should be . Because of this, and the fact that there are four circles, we write Solving for , we obtain , where with , we get , and from here, we simplify and see that
Note: To be more rigorous, note that since if clearly the probability is greater than . This would make sure the above solution works, as if there is overlap with the quartercircles.
Solution 2: As in the previous solution, we obtain the equation , which simplifies to . Since is slightly more than is slightly less than . We notice that than , so is roughly
Define . How many integers are there such that ?
- A.
- B.
- C.
- D.
- E.
Solution 1: Notice that is a product of many integers. We either need one factor to be 0 or an odd number of negative factors. Case 1: There are 100 integers for which Case 2: For there to be an odd number of negative factors, must be between an odd number squared and an even number squared. This means that there are total possible values of . Simplifying, there are 5000 possible numbers. Summing, there are (E) 5100 total possible values of .
Solution 2: Notice that is nonpositive when is between and and and (inclusive), which means that the amount of values equals This reduces to
Let be an ordered quadruple of not necessarily distinct integers, each one of them in the set . For how many such quadruples is it true that is odd? (For example, is one such quadruple, because is odd.)
- A.
- B.
- C.
- D.
- E.
Solution 1 (Parity): In order for to be odd, consider parity. We must have (even)(odd) or (odd)-(even). There are ways to pick numbers to obtain an even product. There are ways to obtain an odd product. Therefore, the total amount of ways to make odd Solution 2 (Basically Solution 1 but more in depth): Consider parity. We need exactly one term to be odd, one term to be even. Because of symmetry, we can set to be odd and to be even, then multiply by 2 . If is odd, both and must be odd, therefore there are possibilities for . Consider . Let us say that is even. Then there are possibilities for . However, can be odd, in which case we have more possibilities for . Thus there are 12 ways for us to choose and 4 ways for us to choose . Therefore, also considering symmetry, we have total values of
As shown in the figure below, a regular dodecahedron (the polyhedron consisting of congruent regular pentagonal faces) floats in empty space with two horizontal faces. Note that there is a ring of five slanted faces adjacent to the top face, and a ring of five slanted faces adjacent to the bottom face. How many ways are there to move from the top face to the bottom face via a sequence of adjacent faces so that each face is visited at most once and moves are not permitted from the bottom ring to the top ring?
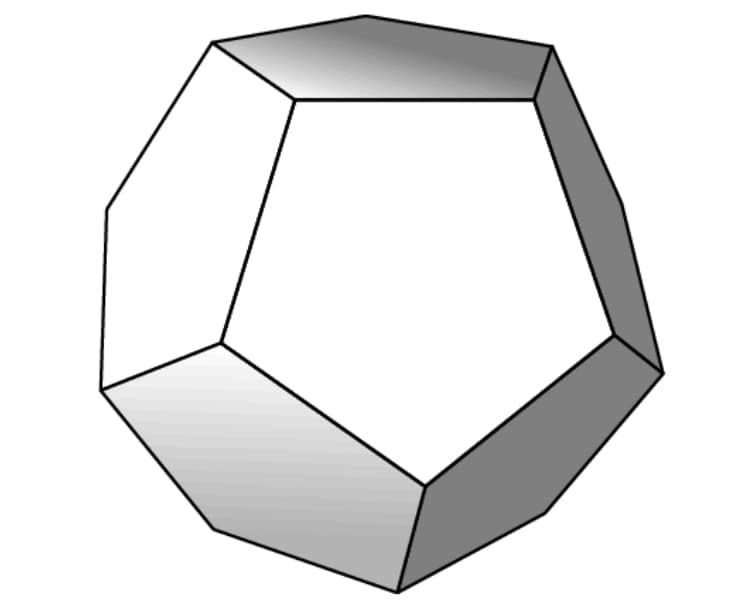
- A.
- B.
- C.
- D.
- E.
Solution 1: Since we start at the top face and end at the bottom face without moving from the lower ring to the upper ring or revisiting a face, our journey must consist of the top face, a series of faces in the upper ring, a series of faces in the lower ring, and the bottom face, in that order.
We have choices for which face we visit first on the top ring. From there, we have choices for how far around the top ring we go before moving down: , or 4 faces around clockwise, , or 4 faces around counterclockwise, or immediately going down to the lower ring without visiting any other faces in the upper ring. We then have choices for which lower ring face to visit first (since every upperring face is adjacent to exactly lower-ring faces) and then once again 9 choices for how to travel around the lower ring. We then proceed to the bottom face, completing the trip. Multiplying together all the numbers of choices we have, we
Solution 2:
Swap the faces as vertices and the vertices as faces. Then, this problem is the same as 2016 AIME I #3which had an answer (E) 810 .
Quadrilateral satisfies , and . Diagonals and intersect at point , and . What is the area of quadrilateral ?
- A.
- B.
- C.
- D.
- E.
Solution 1:
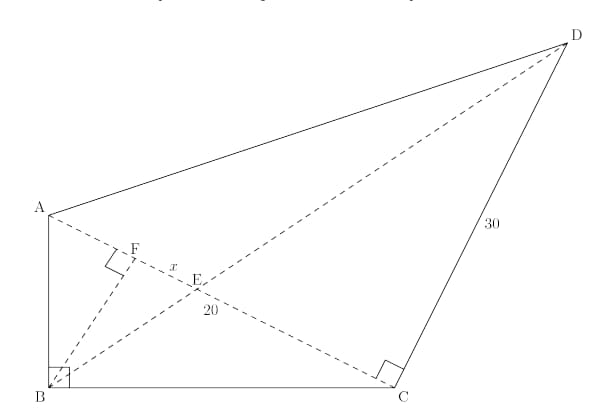
It's crucial to draw a good diagram for this one. Since and , we get . Now we need to find to get the area of the whole quadrilateral. Drop an altitude from to and call the point of intersection . Let . Since , then . By dropping this altitude, we can also see two similar triangles, and . Since is , and , we get that . Now, if we redraw another diagram just of , we get that . Now expanding, simplifying, and dividing by the GCF, we get . This factors to . Since lengths cannot be negative, . Since . So
Solution 2 (Pro Guessing Strats): We know that the big triangle has area 300 . Use the answer choices which would mean that the area of the little triangle is a multiple of 10 . Thus the product of the legs is a multiple of 20 . Guess that the legs are equal to and , and because the hypotenuse is 20 we get . Testing small numbers, we get that when and is indeed a square. The area of the triangle is thus 60 , so the answer is (D) 360
There exists a unique strictly increasing sequence of nonnegative integers such that . What is ?
- A.
- B.
- C.
- D.
- E.
Solution 1: First, substitute with . Then, the given equation becomes . Now consider only . This equals . Note that equals , since the sum of a geometric sequence is . Thus, we can see that forms the sum of 17 different powers of 2 . Applying the same method to each of , we can see that each of the pairs forms the sum of 17 different powers of 2. This gives us . But we must count also the term. Thus, Our answer
Solution 2: (This is similar to solution 1) Let . Then, . The LHS can be rewritten as Plugging back in for , we have When expanded, this will have terms. Therefore, our answer is
For how many positive integers is not divisible by ?(Recall that is the greatest integer less than or equal to .)
- A.
- B.
- C.
- D.
- E.
Solution 1 (Casework):
Expression:
Solution: Let Since , for any integer , the difference between the largest and smallest terms before the function is applied is less than or equal to , and thus the terms must have a range of 1 or less after the function is applied.
This means that for every integer , 998 - if is an integer and , then the three terms in the expression above must be ,- if is an integer because , then will be an integer and will be 1 greater than ; thus the three terms in the expression must be , 999 - if is an integer, then the three terms in the expression above must be , - if is an integer, then the three terms in the expression above must be , and - if none of expression above must be .
The last statement is true because in order for the terms to be different, there must be some integer in the interval or the interval .
However, this means that multiplying the integer interval by should produce a new integer between 998 and 999 or 999 and 1000 , exclusive, but because no such integers exist, the terms cannot be different, and thus, must be equal. - Note that does not work; to prove this, we just have to substitute 1 for in the expression.
This gives us which is divisible by 3 . Now, we test the five cases listed above (where )
Case 1: divides 998 and As mentioned above, the three terms in the expression are , so the sum is , which is divisible by 3 . Therefore, the first case does not work (0 cases).
Case 2: divides 998 and As mentioned above, in this case the terms must be , which means the sum is , so the expression is not divisible by 3 . Therefore, this is 1 case that works.
Case 3: divides 999 Because divides 999 , the number of possibilities for is the same as the number of factors of 999 . So, the total number of factors of 999 is . However, we have to subtract 1 , because the case does not work, as mentioned previously. This leaves cases.
Case 4: divides 1000 Because divides 1000 , the number of possibilities for is the same as the number of factors of 1000 . . So, the total number of factors of 1000 is . Again, we have to subtract 1 , so this leaves cases. We have also overcounted the factor 2 , as it has been counted as a factor of 1000 and as a separate case (Case 2). , so there are actually 14 valid cases.
Case 5: divides none of Similar to Case 1, the value of the terms of the expression are . The sum is , which is divisible by 3 , so this case does not work (0 cases). Now that we have counted all of the cases, we add them. , so the answer is
Solution 2 (Solution 1 but simpler): * Note that this solution does not count a majority of cases that are important to consider in similar problems, though they are not needed for this problem, and therefore it may not work with other, similar problems. Notice that you only need to count the number of factors of 1000 and 999 , excluding 1. 1000 has 16 factors, and 999 has 8 . Adding them gives you 24 , but you need to subtract 2 since 1 does not work. Therefore, the answer is (A) 22 .
Let be the triangle in the coordinate plane with vertices , and . Consider the following five isometries (rigid transformations) of the plane: rotations of , and counterclockwise around the origin, reflection across the -axis, and reflection across the -axis. How many of the sequences of three of these transformations (not necessarily distinct) will return to its original position? (For example, a rotation, followed by a reflection across the -axis, followed by a reflection across the -axis will return to its original position, but a rotation, followed by a reflection across the -axis, followed by another reflection across the -axis will not return to its original position.)
- A.
- B.
- C.
- D.
- E.
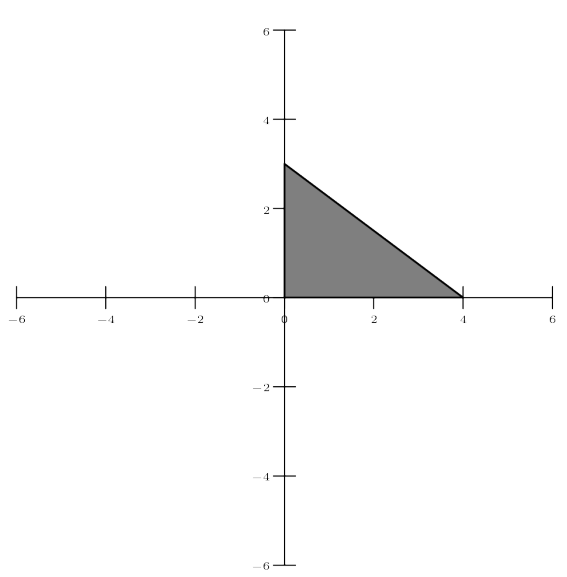
Solution 1:
First, any combination of motions we can make must reflect an even number of times. This is because every time we reflect , it changes orientation. Once has been flipped once, no combination of rotations will put it back in place because it is the mirror image; however, flipping it again changes it back to the original orientation. Since we are only allowed 3 transformations and an even number of them must be reflections, we either reflect times or 2 times.
Case 1: 0 reflections on In this case, we must use 3 rotations to return to its original position. Notice that our set of rotations, , contains every multiple of except for . We can start with any two rotations in and there must be exactly one such that we can use the three rotations . That way, the composition of rotations yields a full rotation. For example, if , then , so and the rotations yields a full rotation. The only case in which this fails is when would have to equal . This happens when namely, , or . However, we can simply subtract these three cases from the total. Selecting yields choices, and with that fail, we are left with combinations for case 1 .
Case 2: 2 reflections on In this case, we first eliminate the possibility of having two of the same reflection. Since two reflections across the -axis maps back to itself, inserting a rotation before, between, or after these two reflections would change 's final location, meaning that any combination involving two reflections across the -axis would not map back to itself. The same applies to two reflections across the -axis. Therefore, we must use one reflection about the -axis, one reflection about the -axis, and one rotation. Since a reflection about the -axis changes the sign of the component, a reflection about the -axis changes the sign of the component, and a rotation changes both signs, these three transformation composed (in any order) will suffice. It is therefore only a question of arranging the three, giving us combinations for case 2 . Combining both cases we get (A) 12
Solution 2(Rewording solution 1): As in the previous solution, note that we must have either or reflections because of orientation since reflection changes orientation that is impossible to fix by rotation. We also know we can't have the same reflection twice, since that would give a net of no change and would require an identity rotation. Suppose there are no reflections. Denote as as , and as , just for simplification purposes. We want a combination of of these that will sum to either or and is impossible since the minimum is and the max is 9). can be achieved with any permutation of and can be achieved with any permutation of . This case can be done in ways. Suppose there are two reflections. As noted already, they must be different, and as a result will take the triangle to the opposite side of the origin if we don't do any rotation. We have rotation left that we can do though, and the only one that will return to the original position is , which is AKA reflection across origin. Therefore, since all transformations are distinct. The three transformations can be applied anywhere since they are commutative(think quadrants). This gives 6 ways.
Let be the least positive integer greater than for which
and .
What is the sum of the digits of ?
- A.
- B.
- C.
- D.
- E.
Solution 1: We know that , so we can write . Simplifying, we get . Similarly, we can write or . Solving these two modular congruences, which we know is the only solution by CRT (Chinese Remainder Theorem). Now, since the problem is asking for the least positive integer greater than 1000 , we find the least solution is . However, we are have not considered cases where or . so we try so again we add 420 to . It turns out that does indeed satisfy the original conditions, so our answer is (C) 18
Solution 2 (bashing): We are given that and . This tells us that is divisible by but not . It also tells us that is divisible by but not . Starting, we find the least value of which is divisible by which satisfies the conditions for , which is , making . We then now keep on adding until we get a number which satisfies the second equation. This number turns out to be , whose digits add up to (C) 18
Jason rolls three fair standard six-sided dice. Then he looks at the rolls and chooses a subset of the dice (possibly empty, possibly all three dice) to reroll. After rerolling, he wins if and only if the sum of the numbers face up on the three dice is exactly . Jason always plays to optimize his chances of winning. What is the probability that he chooses to reroll exactly two of the dice?
- A.
- B.
- C.
- D.
- E.
Solution 1:
Consider the probability that rolling two dice gives a sum of , where . There are pairs that satisfy this, namely , out of possible pairs. The probability is . Therefore, if one die has a value of and Jason rerolls the other two dice, then the probability of winning is .
In order to maximize the probability of winning, must be minimized. This means that if Jason rerolls two dice, he must choose the two dice with the maximum values.
Thus, we can let call , and respectively. Consider the case when . If , then we do not need to reroll any dice. Otherwise, if we reroll one die, we can roll dice in the hope that we get the value that makes the sum of the three dice 7 . This happens with probability . If we reroll two dice, we will roll and , and the probability of winning is , as stated above.
However, , so rolling one die is always better than rolling two dice if
Now consider the case where . Rerolling one die will not help us win since the sum of the three dice will always be greater than 7 . If we reroll two dice, the probability of winning is, once again, . To find the probability of winning if we reroll all three dice, we can let each dice have 1 dot and find the number of ways to distribute the remaining 4 dots. By Stars and Bars, there In order for rolling two dice to be more favorable than rolling three dice, Thus, rerolling two dice is optimal if and only if and . The possible triplets that satisfy these conditions, and the number of ways they can be permuted, There are ways in which rerolling two dice is optimal, out of possibilities, Therefore, the probability that Jason will reroll two dice is (A)
Solution 2:
We count the numerator. Jason will pick up no dice if he already has a as a sum. We need to assume he does not have a to begin with. If Jason decides to pick up all the dice to re-roll, by Stars and Bars(or whatever), there will be bars and stars ( of them need to be guaranteed because a roll is at least ) for a probability of . If Jason picks up dice and leaves a die showing , he will need the other two to sum to . This happens with probability for integers . If the roll is not , Jason will pick up exactly one die to re-roll if there can remain two other dice with sum less than , since this will give him a chance which is a larger probability than all the cases unless he has a to begin with. We have . We count the underlined part's frequency for the numerator without upsetting the probability greater than it. Let be the roll we keep. We know is at most since would cause Jason to pick up all the dice. When , there are choices for whether it is rolled , , or , and in this case the other two rolls have to be at least (or he would have only picked up ). This give ways.
Similarly, gives because the can be rolled in places and the other two rolls are at least 5. gives . Summing together gives the numerator of 42 . The denominator is , so we
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
