2020 AMC 10 B
Complete problem set with solutions and individual problem pages
What is the value of (2020 AMC 10B, Question #1)
- A.
- B.
- C.
- D.
- E.
We know that when we subtract negative numbers, The equation becomes
Carl has cubes each having side length , and Kate has cubes each having side length . What is the total volume of these cubes?(2020 AMC 10B, Question #2)
- A.
- B.
- C.
- D.
- E.
A cube with side length has volume , so of these will have a total volume of .
A cube with side length has volume , so of these will have a total volume of .
The ratio of to is , the ratio of to is , and the ratio of to is . What is the ratio of Wto ? (2020 AMC 10B, Question #3)
- A.
- B.
- C.
- D.
- E.
Solution 1:
WLOG, let and . Since the ratio of to is , we can substitute in the value of to get The ratio of is , so The ratio of to is then so our answer is (E)
Solution 2:
We need to somehow link all three of the ratios together. We can start by connecting the last two ratios together by multiplying the last ratio by two. , and since , we can link them together to get . Finally, since , we can link this again to get: , so
The acute angles of a right triangle are and , where and both and are prime numbers. What is the least possible value of ?(2020 AMC 10B, Question #4)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Since the three angles of a triangle add up to and one of the angles is because it's a right triangle, . The greatest prime number less than 90 is 89 . If , then , which is not prime. The next greatest prime number less than 90 is 83 . If , then , which IS prime, so we have our answer (D) 7
Solution 2:
Looking at the answer choices, only and are coprime to . Testing , the smaller angle, makes the other angle which is prime, therefore our answer
How many distinguishable arrangements are there of brown tile, purple tile, green tiles, and yellow tiles in a row from left to right? (Tiles of the same color are indistinguishable.) (2020 AMC 10B, Question #5)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Let's first find how many possibilities there would be if they were all distinguishable, then divide out the ones we overcounted. There are ways to order objects. However, since there's ways to switch the yellow tiles around without changing anything (since they're indistinguishable) and ways to order the green tiles, we have to divide out these possibilities.
Solution 2:
We can repeat chooses extensively to find the answer. There are 7 choose 3 ways to arrange the brown tiles which is 35 . Then from the remaining tiles there are 4 choose ways to arrange the red tiles. And now from the remaining two tiles and two slots we can see there are two ways to arrange the purple and brown tiles, giving us an answer
Driving along a highway, Megan noticed that her odometer showed (miles). This number is a palindrome-it reads the same forward and backward. Then hours later, the odometer displayed the next higher palindrome. What was her average speed, in miles per hour, during this -hour period?(2020 AMC 10B, Question #6)
- A.
- B.
- C.
- D.
- E.
In order to get the smallest palindrome greater than , we need to raise the middle digit. If we were to raise any of the digits after the middle, we would be forced to also raise a digit before the middle to keep it a palindrome, making it unnecessarily larger. So we raise to the next largest value, , but obviously, that's not how place value works, so we're in the now. To keep this a palindrome, our number is now . So Megan drove miles. Since this happened over 2 hours, she drove at (B) 55 mph.
How many positive even multiples of less than are perfect squares? (2020 AMC 10B, Question #7)
- A.
- B.
- C.
- D.
- E.
Any even multiple of is a multiple of , so we need to find multiples of that are perfect squares and less than . Any solution that we want will be in the form , where is a positive integer. The smallest possible value is at , and the largest is at (where the expression equals 1764 ). Therefore, there are a total of (A) 7 possible numbers.
Points and lie in a plane with . How many locations for point in this plane are there such that the triangle with vertices , and is a right triangle with area square units?(2020 AMC 10B, Question #8)
- A.
- B.
- C.
- D.
- E.
Solution 1:
There are 3 options here: 1. is the right angle. It's clear that there are points that fit this, one that's directly to the right of and one that's directly to the left. We don't need to find the length, we just need to know that it is possible, which it is. 2. is the right angle. Using the exact same reasoning, there are also solutions for this one. 3 . The new point is the right angle. (Diagram temporarily removed due to asymptote error) The diagram looks something like this. We know that the altitude to base must be since the area is . From here, we must see if there are valid triangles that satisfy the necessary requirements. First of all, area. Next, from the Pythagorean Theorem. From here, we must look to see if there are valid solutions. There are multiple ways to do this: Recognizing min and max: We know that the minimum value of is when . In this case, the equation becomes , which is LESS than . The equation becomes , which is obviously greater than 64 . We can conclude that there are values for and in between that satisfy the Pythagorean Theorem. And since , the triangle is not isoceles, meaning we could reflect it over and/or the line perpendicular to for a total of 4 triangles this case.
Solution 2:
Note that line segment can either be the shorter leg, longer leg or the hypotenuse. If it is the shorter leg, there are two possible points for that can satisfy the requirements - that being above or below . As such, there are 2 ways for this case. Similarly, one can find that there are also 2 ways for point to lie if is the longer leg. If it is a hypotenuse, then there are 4 possible points because the arrangement of the shorter and longer legs can be switched, and can be either above or below the line segment. Therefore, the answer is
How many ordered pairs of integers satisfy the equation (2020 AMC 10B, Question #9)
- A.
- B.
- C.
- D.
- E.
infinitely many
Solution 1: Rearranging the terms and and completing the square for yields the result . Then, notice that can only be and because any value of that is greater than will cause the term to be less than 0 , which is impossible as must be real. Therefore, plugging in the above values for gives the ordered pairs , and gives a total of (D)4 ordered pairs.
Solution 2:
Bringing all of the terms to the LHS, we see a quadratic equation in terms of . Applying the quadratic formula, we order for to be real, which it must be given the stipulation that we are seeking integral answers, we know that the discriminant, must be nonnegative. Therefore, we see that we must split the inequality into a compound, resulting in The only integers that satisfy this are . Plugging these values back into the quadratic equation, we see that both produce a discriminant of 0 , meaning that there is only 1 solution for . If , then the discriminant is nonzero, therefore resulting in two solutions for . Thus, the answer is
A three-quarter sector of a circle of radius inches together with its interior can be rolled up to form the lateral surface area of a right circular cone by taping together along the two radii shown. What is the volume of the cone in cubic inches? (2020 AMC 10B, Question #10)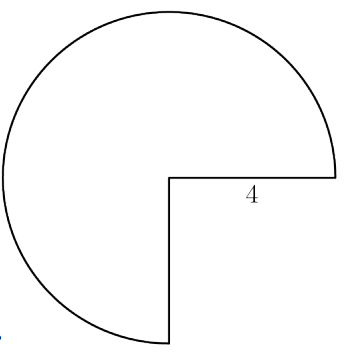
- A.
- B.
- C.
- D.
- E.
Solution 1: Notice that when the cone is created, the radius of the circle will become the slant height of the cone and the intact circumference of the circle will become the circumference of the base of the cone. We can calculate that the intact circumference of the circle is . Since that is also equal to the circumference of the cone, the radius of the cone is 3 . We also have that the slant height of the cone is 4 . Therefore, we use the Pythagorean Theorem to calculate that the height of the cone is . The volume of the cone is
Solution 2 (Last Resort/Cheap):
Using a ruler, measure a circle of radius 4 and cut out the circle and then the quarter missing. Then, fold it into a cone and measure the diameter to be 6 . You can form a right triangle with sides 3,4 , and then through the Pythagorean theorem the height is found to be . The volume of a cone is . Plugging in we find
Ms. Carr asks her students to read any of the books on a reading list. Harold randomly selects books from this list, and Betty does the same. What is the probability that there are exactly books that they both select?(2020 AMC 10B, Question #11)
- A.
- B.
- C.
- D.
- E.
We don't care about which books Harold selects. We just care that Betty picks 2 books from Harold's list and 3 that aren't on Harold's list. The total amount of combinations of books that Betty can select ways for Betty to choose 2 of the books that are on Harold's list. From the remàining 5 books that aren't on Hàrold's list, there
The decimal representation of consists of a string of zeros after the decimal point, followed by a and then several more digits. How many zeros are in that initial string of zeros after the decimal point?(2020 AMC 10B, Question #12)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Now we do some estimation. Notice that , which means that is a little more than . Multiplying it with , we get that the denominator is about . Notice that when we divide by an digit number, there are zeros before the first nonzero digit. This means that when we divide by the digit , there are integer decimal point.
Solution 2:
First rewrite as . Then, we know that when we write this in decimal form, there will be 40 digits after the decimal point. Therefore, we just have to find the number of digits in . and memming (alternatively use the fact that ), digits. Our answer is (D) 26
Andy the Ant lives on a coordinate plane and is currently at facing east (that is, in the positive -direction). Andy moves unit and then turns degrees left. From there, Andy moves units (north) and then turns degrees left. He then moves units (west) and again turns degrees left. Andy continues his progress, increasing his distance each time by unit and always turning left. What is the location of the point at which Andy makes the left turn?(2020 AMC 10B, Question #13)
- A.
- B.
- C.
- D.
- E.
You can find that every four moves both coordinates decrease by . Therefore, both coordinates need to decrease by two times. You subtract, giving you the answer of (B)
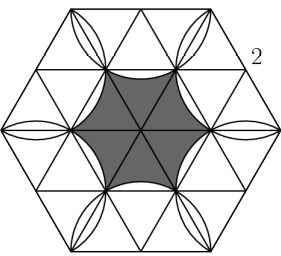
As shown in the figure below, six semicircles lie in the interior of a regular hexagon with side length so that the diameters of the semicircles coincide with the sides of the hexagon. What is the area of the shaded region - inside the hexagon but outside all of the semicircles?(2020 AMC 10B, Question #14)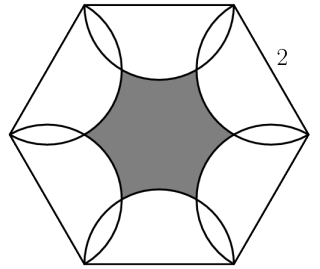
- A.
- B.
- C.
- D.
- E.
Solution 1:
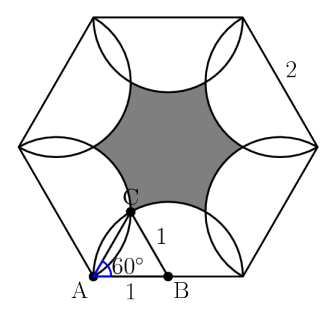 Let point be a vertex of the regular hexagon, let point be the midpoint of the line connecting point and a neighboring vertex, and let point be the second intersection of the two semicircles that pass through point . Then, , since is the center of the semicircle with radius 1 that lies on, , since is the center of the semicircle with radius 1 that lies on, and , as a regular hexagon has angles of 120 , and is half of any angle in this hexagon. Now, using the sine law, , so . Since the angles in a triangle sum to is also . Therefore, is an equilateral triangle with side lengths of .
Let point be a vertex of the regular hexagon, let point be the midpoint of the line connecting point and a neighboring vertex, and let point be the second intersection of the two semicircles that pass through point . Then, , since is the center of the semicircle with radius 1 that lies on, , since is the center of the semicircle with radius 1 that lies on, and , as a regular hexagon has angles of 120 , and is half of any angle in this hexagon. Now, using the sine law, , so . Since the angles in a triangle sum to is also . Therefore, is an equilateral triangle with side lengths of .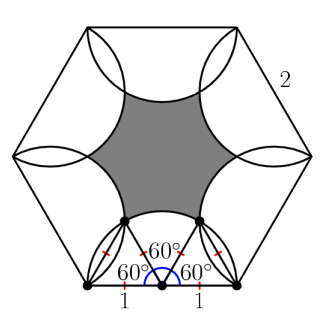 Since the area of a regular hexagon can be found with the formula , where is the side length of the hexagon, the area of this hexagon . is 2 . Since the area of an equilateral triangle can be found with the formula , where is the side length of the equilateral triangle, the area of an equilateral triangle with side lengths of 1 is . Since the area of a circle can be found with the formula , the area of a sixth of a circle with radius 1 is . In each sixth of the hexagon, there of a circle with radius 1 is . In each sixth of the hexagon, there sixth of a circle with radius 1 colored white, with an area of . The rest of the sixth is colored gray. Therefore, the total area that is colored white in each sixth of the hexagon is , which equals , and the total area colored white is , which equals . Since the area colored gray equals the total area of the hexagon minus the area colored white, the area colored gray is , which equals (D)
Since the area of a regular hexagon can be found with the formula , where is the side length of the hexagon, the area of this hexagon . is 2 . Since the area of an equilateral triangle can be found with the formula , where is the side length of the equilateral triangle, the area of an equilateral triangle with side lengths of 1 is . Since the area of a circle can be found with the formula , the area of a sixth of a circle with radius 1 is . In each sixth of the hexagon, there of a circle with radius 1 is . In each sixth of the hexagon, there sixth of a circle with radius 1 colored white, with an area of . The rest of the sixth is colored gray. Therefore, the total area that is colored white in each sixth of the hexagon is , which equals , and the total area colored white is , which equals . Since the area colored gray equals the total area of the hexagon minus the area colored white, the area colored gray is , which equals (D)
Solution 2:
First, subdivide the hexagon into 24 equilateral triangles with side length
Now note that the entire shaded region is just 6 times this part: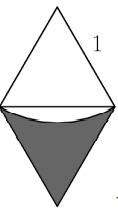
The entire rhombus is just 2 equilatrial triangles with side lengths of 1 , so it has an area of: Hence, the area of the shaded region in that section is For a final area
Steve wrote the digits , and in order repeatedly from left to right, forming a list of digits, beginning . He then erased every third digit from his list (that is, the 3rd, Gth, 9th, .. .digits from the left), then erased every fourth digit from the resulting list (that is, the 4 th, 8 th, 12 th, . . , digits from the left in what remained), and then erased every fifth digit from what remained at that point. What is the sum of the three digits that were then in the positions ?(2020 AMC 10B, Question #15)
- A.
- B.
- C.
- D.
- E.
After erasing every third digit, the list becomes . repeated. After erasing every fourth digit from this list, the list becomes . . repeated. Finally, after erasing every fifth digit from this list, the list becomes . . repeated. Since this list repeats every digits and since are respectively in , we have that the ,, and digits are the , , and digits respectively. It follows that the answer is .
Bela and Jenn play the following game on the closed interval of the real number line, where is a fixed integer greater than . They take turns playing, with Bela going first. At his first turn, Bela chooses any real number in the interval . Thereafter, the player whose turn it is chooses a real number that is more than one unit away from all numbers previously chosen by either player. A player unable to choose such a number loses. Using optimal strategy, which player will win the game?(2020 AMC 10B, Question #16)
- A.
Bela will always win.
- B.
Jenn will always win
- C.
Bela will win if and only if is odd
- D.
Jenn will win if and only if is odd.
- E.
Jenn will win if and only if .
Solution 1:
Notice that to use the optimal strategy to win the game, Bela must select the middle number in the range and then mirror whatever number Jenn selects. Therefore, if Jenn can select a number within the range, so can Bela. Jenn will always be the first person to run out of a number to choose, so the answer is (A)Bela will always win.
Solution 2 (Guessing): First of all, realize that the value of should have no effect on the strategy at all. This is because they can choose real numbers, not integers, so even if is odd, for example, they can still go halfway. Similarly, there is no reason the strategy would change when .
So we are left with (A) and (B). From here it is best to try out random numbers and try to find the strategy that will let Bela win, but if you can't find it, realize that it is more likely the answer is (A) Bela will always win since Bela has the first move and thus has more control.
There are people standing equally spaced around a circle. Each person knows exactly ' of the other Gpeople: the " people standing next to her or him as well as the person directly across the circle. How many ways are there for the people to split up into pairs so that the members of each pair know each other?(2020 AMC 10B, Question #17)
- A.
- B.
- C.
- D.
- E.
Let us use casework on the number of diagonals. Case diagonals There are ways: either pairs with pairs with , and so on or pairs with pairs with , etc.
Case diagonal There are possible diagonals to draw (everyone else pairs with the person next to them. Note that there cannot be diagonals. Case diagonals Note that there cannot be a case with diagonals because then there would have to be diagonals for the two remaining people, thus a contradiction. Case diagonals There is way to do this. Thus, in total there are possible ways.
An urn contains one red ball and one blue ball. A box of extra red and blue balls lie nearhy. Genrge performs the following operation four times: he draws a hall from the urn at random and then takes a ball of the same color from the box and returns those two matching balls to the urn. After the four iterations the urn contains six balls. What is the probability that the urn contains three balls of each color?(2020 AMC 10B, Question #18)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Let denote that George selects a red ball and that he selects a blue one. Now, in order to get 3 balls of each color, he needs 2 more of both and . There are 6 cases: can confirm that there are only 6 since ). However we can clump and together since they are equivalent by symmetry.
CASE 1: and Let's find the probability that he picks the balls in the order of . The probability that the first ball he picks is red is . Now there are 2 reds and 1 blue in the urn. The probability that he picks red again is now .
There are 3 reds and 1 blue now. The probability that he picks a blue is . Finally, there are 3 reds and 2 blues. The probability that he picks a blue is . So the probability that the case happens is . However, since the case is the exact same by symmetry, case 1 has a probability of chance of happening.
CASE 2:RBRB and Let's find the probability that he picks the balls in the order of . The probability that the first ball he picks is red is . Now there are 2 reds and 1 blue in the urn. The probability that he picks blue is .
There are 2 reds and 2 blues now. The probability that he picks a red is . Finally, there are 3 reds and 2 blues. The probability that he picks a blue is . So the probability that the case happens . However, since the case is the exact is . However, since the Rcase is the exact same by symmetry, case 2 has a probability of chance of happening.
CASE 3: and Let's find the probability that he picks the balls in the order of . The probability that the first ball he picks is red is . Now there are 2 reds and 1 blue in the urn. The probability that he picks blue is
There are 2 reds and 2 blues now. The probability that he picks a blue is . Finally, there are 2 reds and 3 blues. The probability that he picks a red is . So the probability that the case happens is . However, since the case is the exact is . However, since the case is the exact same by symmetry, case 3 has a probability of chance of happening.
Adding up the cases, we have (B)
Solution 2: We know that we need to find the probability of adding 2 red and 2 blue balls in some order. There are 6 ways to do this, since there are ways to arrange in some order. We will show that the probability for each of these 6 ways is the same.
We first note that the denominators should be counted by the same number. This number is . This is because , and 5 represent how many choices there are for the four steps. No matter what the step involves numbers to choose from. The numerators are the number of successful operations. No matter the order, the first time a red is added will come from 1 choice and the second time will come from 2 choices, since that is how many reds are in the urn originally. The same goes for the blue ones. The numerator must equal . Therefore, the probability for each of the orderings of is is . There are 6 of these, so the total probability is (B)
In a certain card game, a player is dealt a hand of cards from a deck of distinct cards. The number of distinct (unordered) hands that can be dealt to the player can be written as . What is the digit ?(2020 AMC 10B, Question #19)
- A.
- B.
- C.
- D.
- E.
Solution 1:
We're looking for the amount of ways we can get 10 cards from a deck of 52 , which is represented by . We need to get rid of the multiples of 3 , which will subsequently get rid of the multiples of 9 (if we didn't, the zeroes would mess with the equation since you can't divide by 0 ) leaves us with . Converting these into , we have
Solution 2:
Since this number is divisible by but not , the last digits must be divisible by but the last 3 digits cannot be divisible by . This narrows the options down to and . Also, the number cannot be divisible by . Adding up the digits, we get . If , then the expression equals , a multiple of . This would mean that the entire number would be divisible by , which is not what we want. Therefore, the only option is (A)2.
Let be a right rectangular prism (box) with edges lengths , and , together with its interior. For real , let be the set of points in dimensional space that lie within a distance of some point . The volume of can be expressed as , where , and are positive real numbers. What is (2020 AMC 10B, Question #20)
- A.
- B.
- C.
- D.
- E.
Split into 4 regions: 1. The rectangular prism itself 2. The extensions of the faces of 3. The quarter cylinders at each edge of 4. The one-eighth spheres at each corner of Region 1: The volume of is 12 , so Region 2: The volume is equal to the surface area of times . The surface area can be computed to be , so . Region 3 : The volume of each quarter cylinder is equal to . The sum of all such cylinders must equal times the sum of the edge lengths. This can be computed as , so the sum of the volumes of the quarter cylinders is , so
Region 4: There is an eighth of a sphere of radius at each corner. Since there are 8 corners, these add up to one full sphere of radius . The volume of this sphere is , so . Using these values,
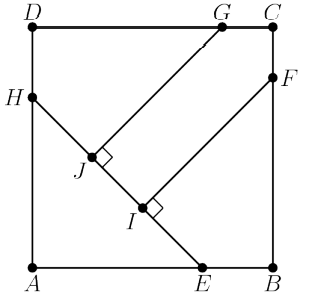
In square , points and lie on and , respectively, so that . Points and lie on and , respectively, and points and lie on so that and . See the figure below. Triangle , quadrilateral , quadrilateral , and pentagon each has area 1 . What is ?(2020 AMC 10B, Question #21)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Since the total area is , the side length of square is 2 . We see that since triangle is a right isosceles triangle with area , we can determine sides and both to be . Now, consider extending and until they intersect. Let the point of intersection be . We note that is also a right isosceles triangle with side and find it's area to be . Now, we notice that is also a right isosceles triangle and find it's area to be . This is also equal to or . Since we are looking for , we want two times this. That gives(B)
Solution 2:
Since this is a geometry problem involving sides, and we know that is 2 , we can use our ruler and find the ratio between and . Measuring(on the booklet), we get that is about inches and is about inches. Thus, we can then multiply the length of by the ratio of , of which we then get . We take the square of that and of , and the closest answer to that is (B) . (Note that this is just a strategy I happened to use that worked. Do not press your luck with this strategy, for it was a lucky quess)
What is the remainder when is divided by ?(2020 AMC 10B, Question #22)
- A.
- B.
- C.
- D.
- E.
Solution 1: Let . We are now looking for the remainder of We could proceed with polynomial division, but the denominator looks awfully similar to the Sophie Germain Identity, which states that Let's use the identity, with and , so we have Rearranging, we can see that this is exactly what we need: Since the first half divides cleanly as shown earlier, the remainder must be (D) 201.
Solution 2:
Similar to Solution 1 , let . It suffices to find remainder of . of . Dividing polynomials results in a remainder of (D) 201
Square in the coordinate plane has vertices at the points , and . Consider the following four transformations: , a rotation of counterclockwise around the origin; , a rotation of clockwise around the origin; , a reflection across the -axis; and , a reflection across the -axis. Each of these transformations maps the squares onto itself, but the positions of the labeled vertices will change. For example, applying and then would send the vertex at to and would send the vertex at to itself. How many sequences of 20 transtormations chosen from will send all of the labeled vertices back to their original positions? (For example, is one sequence of transformations that will send the vertices back to their original positions.)(2020 AMC 10B, Question #23)
- A.
- B.
- C.
- D.
- E.
Solution 1: Let (+) denote counterclockwise/starting orientation and (-) denote clockwise orientation. Let , and 4 denote which quadrant is in.
Realize that from any odd quadrant and any orientation, the 4 transformations result in some permutation of . The same goes that from any even quadrant and any orientation, the 4 transformations result in some permutation of . We start our first 19 moves by doing whatever we want, 4 choices each time. Since 19 is odd, we must end up on an even quadrant.
As said above, we know that exactly one of the four transformations will give us , and we must use that transformation. Thus
Solution 2: Hopefully, someone will think of a better one, but here is an indirect answer, use only if you are really desperate. 20 moves can be made, and each move have 4 choices, so a total of moves. First, after the 20 moves, Point can only be in first quadrant or third quadrant . Only the one in the first quadrant works, so divide by 2 . Now, must be in the opposite quadrant as A. B can be either in the second ) or fourth quadrant , but we want it to be in the second quadrant, so divide by 2 again. Now as and satisfy the conditions, and will also be at their original spot. . The answer is
How many positive integers satisfy ?(Recall that is the greatest integer less than or equal to .)(2020 AMC 10B, Question #24)
- A.
- B.
- C.
- D.
- E.
Solution 1:
First notice that the graphs of and intersect at 2 points. Then, notice that must be an integer. This means that is congruent to .
For the first intersection, testing the first few values of (adding 70 to each time and noticing the left side increases by 1 each time) yields and . timating from the graph can narrow down the other cases, being . This results in a total of 6 cases, for an answer of
Solution 2 (Graphing):
One intuitive approach to the question is graphing. Obviously, you should know what the graph of the square root function is, and if any function is floored (meaning it is taken to the greatest integer less than a value), a stair-like figure should appear. The other function is simply a line with a slope of . If you precisely draw out the two regions of the graph where the derivative of the square function nears the derivative of the linear function, you can now deduce that 3 values of intersection lay closer to the left side of the stair, and 3 values lay closer to the right side of the stair. With meticulous graphing, you can realize that the answer is . A in-depth graph with intersection points is linked below. https://www.desmos.com/calculator/e5wk9adbuk
Let denote the number of ways of writing the positive integer as a product ,where , the are integers strictly greater than , and the order in which the factors are listed matters (that is, two representations that differ only in the order of the factors are counted as distinct). For example, the number 6 can be written as , and , so . What is ?(2020 AMC 10B, Question #25)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Note that . Since there are at most six not necessarily distinct factors multiplying to 96 , we have six cases. . Now we look at each of the six cases. : we see that there is 1 way, merely 96 . : This way, we have the 3 in one slot and 2 in another, and symmetry. The four other 2 's leave us with 5 ways and symmetry doubles us so we have 10 . : We have as our baseline. We need to multiply by 2 in 3 places, and see that we can split the remaining three powers of 2 in a manner that is or . A split has ways of happening and symmetry; and symmetry), a split has ways of happening (due to all being distinct) and a split has 3 ways of happening ( and symmetry) so in this case we have ways. : We have as our baseline, and for the two other 2 s, we have a or split. The former grants us ways and symmetry and and symmetry) and the latter grants us also ways and symmetry and and symmetry) for a total of ways. : We have as our baseline and one place to put the last two: on another two or on the three. On the three gives us 5 ways due to symmetry and on another two gives us ways due to symmetry. Thus, we have ways. We have and symmetry and no more twos to multiply, so by symmetry, we have 6 ways. Thus, adding, we
Solution 2:
As before, note that , and we need to consider 6 different cases, one for each possible value of , the number of factors in our factorization. However, instead of looking at each individually, find a general form for the number of possible factorizations with factors. First, the factorization needs to contain one factor that is itself a multiple of 3 , and there are to choose from, and the rest must contain at least one factor of 2 . Next, consider the remaining factors of 2 left to assign to the factors. Using stars and bars, the number of ways to do this makes To obtain the total number of factorizations, add all possible values for k:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
