2019 AMC 10 B
Complete problem set with solutions and individual problem pages
Alicia had two containers. The first was full of water and the second was empty. She poured all the water from the first container into the second container, at which point the second container was full of water. What is the ratio of the volume of the first container to the volume of the second container? (2019 AMC 10B Problem, Question#1)
- A.
- B.
- C.
- D.
- E.
Let the first jar's volume be and the second's be . It is given that . We find that.
We already know that this is the ratio of the smaller to the larger volume because it is less than .
We can set up a ratio to solve this problem. If is the volume of the first container, and is the volume of the second container, then:,
Crossmultiplying allows us to get. Thus the ratio of the volume of the first container to the second container is .
An alternate solution is to plug in some maximum volume for the first container let's say , so there was avolume of in the first container, and then the second container also has a volume of , so you get Thus to answer is .
Consider the statement, "If is not prime, then is prime." Which of the following values of is a counterexample to this statement? (2019 AMC 10B Problem, Question#2)
- A.
- B.
- C.
- D.
- E.
Since a counterexample must be value of which is not prime, must be composite, so we eliminate and . Now we subtract from the remaining answer choices, and we see that the only time is not prime is when .
In a high school with students, of the seniors play a musical instrument, while of the nonseniors do not play a musical instrument. In all, of the students do not play a musical instrument. How many nonseniors play a musical instrument? (2019 AMC 10B Problem, Question#3)
- A.
- B.
- C.
- D.
- E.
of seniors do not play a musical instrument. If we denote as the number of seniors, then ,
,
Thus there are nonseniors. Since of the nonseniors play a musical instrument, .
Let be the number of seniors, and be the number of nonseniors.Then,
Multiplying both sides by gives us ,
Also, because there are students in total.
Solving these system of equations give us ,.
Since of the non-seniors play a musical instrument, the answer is simply of , which gives us .
We can clearly deduce that of the nonseniors do play an instrument, but, since the total percentage of instrument players is , the nonsenior population is quite low. By intuition, we can therefore see that the answer is around or . Testing both of these gives us the answer .
All lines with equation such that ,, form an arithmetic progression pass through a common point. What are the coordinates of that point? (2019 AMC 10B Problem, Question#4)
- A.
- B.
- C.
- D.
- E.
If all lines satisfy the condition, then we can just plug in values for , , and that form an arithmetic progression. Let's use , , , and , , .Then the two lines we get are: Use elimination to deduce and plug this into one of the previous line equations. We get Thus the common point is .
We know that , , and form an arithmetic progression, so if the common difference is , we can say , , , , . Now we have , and expanding gives . Factoring gives . Since this must always be true (regardless of the values of and ), we must have and , so , , , and the common point is .
Triangle lies in the first quadrant. Points , , and are reflected across the line to points , , and , respectively. Assume that none of the vertices of the triangle lie on the line . Which of the following statements is not always true? (2019 AMC 10B Problem, Question#5)
- A.
Tiangle lies in the first quadrant.
- B.
Tiangles and have the same area.
- C.
The slope of line is .
- D.
The slopes of lines and are the same.
- E.
Lines and are perpendicular to each other.
Let's analyze all of the options separately.
: Clearly is true, because a point in the first quadrant will have non-negative and . coordinates, and so its reflection, with the coordinates swapped, will also have nonnegative and coordinates.
: The triangles have the same area, since and are the same tiangle (congruent). More formally, we can say that area is invariant under reflection.
: If point has coordinates , then will have coordinates . The gradient is thus , so this is true. (We know since the question states that none of the points , ,or lies on the line , so there is no risk of division by zero).
: Repeating the argument for , we see that both lines have slope, so this is also true.
: By process of eliminaton,this must now be the answer, Indeed, it point has
coordinates and point has coordinates , then and will, respectively, have coordinates and . The product of the gradients of and is , so in fact these lines are never perpendicuar to each other (using the "negative reciprocal" condition for perpendicularity). Thus the anewer is .
Counterexamples
If and , then the slope of , , is . While the slope of , , is . is the reciprocal of , but it is not the negative reciprocal of . To generalize, let denote the coordinates of point , let denote the coordinates of point , let denote the slope of segment , and let denote the slope of segment ,. Then, the coordinates of are , and of are .
Then, , and .
If and , , and in these cases, the condition is false.
There is a real such that . What is the sum of the digts of ? (2019 AMC 10B Problem, Question#6)
- A.
- B.
- C.
- D.
- E.
,
solving by the quadratic formula. (since clearly )The answer is therefore .
Dividing both sides by gives . since is nonnegative, . The answeris .
Dividing both sides by as before gives , Now factor out , giving . By considering the prime factorization of , a bit of experimentation gives us and , so so the answer is .
Each piece of candy in a store costs a whole number of cents. Casper has exactly enough money to buy either pieces of red candy, pieces of green candy, pieces of blue candy, or pieces of purple candy. A piece of purple candy costs cents. What is the smallest possible value of ? (2019 AMC 10B Problem, Question#7)
- A.
- B.
- C.
- D.
- E.
If he has enough money to buy pieces of red candy, pieces of green candy, and pieces of blue candy, then the smallest amount of money he could have is cents. Since a piece of purpe candy costs cems,the smallest possible value of is .
We simply need to find a value of that is divisible by , , and . Observe that is divisible by and , but not . is divisible by , , and , meaning that we have exact change (in this case, cenis) to buy each type of candy, so the minimum value of is .
The figure below shows a square and four equilateral triangles, with each triangle having a side lying on a side of the square, such that each triangle has side length and the third vertices of the triangles meet at the center of the square. The region inside the square but outside the triangles is shaded. What is the area of the shaded region? (2019 AMC 10B Problem, Question#8)
- A.
- B.
- C.
- D.
- E.
We notice th@t the square can be split into congruent smaller squares, with the altitude of the equilateral triangle being the side of this sm@ller square. Therefore, the area of each shaded part that resides within a square is the total area of the square subtracted from each triangle (which has already been split in half).
When we split an equilateral triangle in half, we get two triangles. Therefore, the altitude, which is also the side length of one of the smaller squares, is . We can then compute the area of the two triangles as .
The area of the each small squares is the square of the side length, . Therefore, the area of the shaded region in each of the four squares is .
since there are of these squares, we muitiply this by to get as our answer.
We can see that the side length of the square is by considering the altitude of the equilateral triangle as in Solution . Using the Pythagorean Theorem, the diagonal of the square is thus . Because of this, the height of one of the four shaded kites is .
Now, we just need to find the length of that kite. By the Pythagorean Theorem again, this length . Now using area length width, the area of one of the four kites is .
The function is defined by for all real numbers , where denotes the greatest integer less than or equal to the real number . What is the range of ? (2019 AMC 10B Problem, Question#9)
- A.
- B.
the set of nonpositive integers
- C.
- D.
- E.
the set of nonnegative integers
There are four cases we need to consider here.
Case : is a positive integer. Without loss of generality, assume .Then .
Case : is a positive fraction. Wihout loss of generality, asume .
Then .
Case : is a negative integer. Without loss of generality, assume .
Then .
Case : is a negative fraction. Without loss of generality, assume .
Then
Thus the range of the function is .
It is easily verifed that when is an integer, is zero. We therefore need only to consider the case when is not an integer.
When is postive, , so
.
When is negative, let be composed of integer part and fractional part (both ):
.
Thus,the range of is .
Note: One could solve the case of as a negative noninteger in this way:
.
In a given plane, points and are units apart. How many points are there in the plane such that the perimeter of is units and the area of is square units? (2019 AMC 10B Problem, Question#10)
- A.
- B.
- C.
- D.
- E.
infnitely many
Notice that whatever point we pick for , will be the base of the triangle. Without loss of generality, let points and be and , since for any other combination of points, we can just rotate the plane to make them and under a new coordinate system. When we pick point , we have to make sure that its coordinate is , because that's the only way the area of the triangle can be .
Now when the perimeter is minimized, by symmetry, we put in the middle, at . We can easily see that and will both be . The perimeter of this minimal tiangle is . which is larger than . Since the minimum perimeter is greater than , there is no triangle that satisfies the condition, giving us .
Without loss of generality, let be a horizontal segment of length . Now realize that has to lie on one of the lines parallel to and vertically units away from it. But is already , and this doesn't form a triangle. Otherwise, without loss of generality, . Dropping altitude , we have a right triangle with hypotenuse and leg , which is clearly impossible, again giving the answer as .
Two jars each contain the same number of marbles, and every marble is either blue or green. In Jar the ratio of blue to green marbles is , and the ratio of blue to green marbles in Jar is . There are green marbles in all. How many more blue marbles are in Jar than in Jar ? (2019 AMC 10B Problem, Question#11)
- A.
- B.
- C.
- D.
- E.
Call the number of marbles in each jar (because the problem specifies that they each contain the same number). Thus, is the number of green marbles in Jar , and is the number of green marbles in Jar . Since , we have , so there are marbles in each jar.
Because is the number of blue marbles in Jar , and is the number of blue marbles in Jar , tere are more mables in Jar than Jar . This means the answers is .
What is the greatest possible sum of the digits in the baseseven representation of a positive integer less than ? (2019 AMC 10B Problem, Question#12)
- A.
- B.
- C.
- D.
- E.
Observe that .To maximize the sum of the digits, we want as many as possible (since is the highest value in base ), and this will occur with either of the numbers or .
Thus, the answer is ..
IronicNinja, edited by some people,
Note: the number can also be , which will also give the answer of .
Note that all base numbers with or more digits are in fact greater than . Since the first answer that is possible using a digit number is , we start with the smallest base number that whose digits sum to , namely , But this is greater than , so we continue by trying ,
which is less than . So the answer is ..
What is the sum of all real numbers for which the median of the numbers , , , , and is equal to the mean of those five numbers? (2019 AMC 10B Problem, Question#13)
- A.
- B.
- C.
- D.
- E.
The mean is .
There are three possibilties for the median: it is either . , or .
Let's start with .
has solution , and the sequence is , , , , , which does have median , so this is a valid solution.
Now let the median be .
give , so the sequence is , , , , , which has median , so this is not valid.
Finally we let the median be .
, and the sequene is , , , , ,
which has median . This case is therefore again not valid.
Hence the only possible vaue of is .
The baseten representation for is ,,,,,, where , , and denote digits that are not given. What is ? (2019 AMC 10B Problem, Question#14)
- A.
- B.
- C.
- D.
- E.
We can figure out by noticing that will end with zeroes, as there are three in its prime factorization. Next, we use the fact that is a mutiple of both and . Their divisibilty rules (see Solution ) tell us that (mod ) and that (mod ) By inspection, we see that , is a valid solution. Therefore the answers .
We know that and are both factors of , Furthermore, we know that , because ends in three zeroes (see Solution ). We can simply use the divisibility rules for and for this problem to find and . For to be divisible by , the sum of digits must simply be divisible by . Summing the digits, we get that must be divisible by . This leaves either or as our answer choice. Now we test for divisibility by . For a number to be divisible by , the alternating sum must be divisible by (for example, with the number , , so is divisible by ). Applying the alternating sum test to this problem, we see that must be divisible by . By inspection, we can see that this holds if and The sum .
Right triangles and have areas and , respectively. side of is congruent to a side of and a different side of is congruent to a different side of . What is the square of the product of the other (third) sides of and ? (2019 AMC 10B Problem, Question#15)
- A.
- B.
- C.
- D.
- E.
First of all, let the two sides which are congruent be and , where . The only way that the conditions of the problem can be satisfied is if is the shorter leg of and the longer leg of , and is the longer leg of and the hypotenuse of .
Notice that this means the value we are looking for is the square of , which is just .
The area conditions give us two equations: and .
This means that and that .
Taking the second equation, we get , so since , .
Since , we got .
The value we are looking for is just so the answer .
Solution by Invoker.
Like in solution , we have and .
Squaring both equations yieds and ,
Let and , Then , and ,
so
We are looking for the value of ,so the answers is .
Firstly, let the right triangles be and , with being the smaller triangle. As ir Solution , let and , Additionally let and ,
We are given that and , so using , we have and . Dviding the two equations, we get , so ,
Thus is a right triangle, meaning that . Now by the Pyhagorean Theorem in , .
The problem requires the square of the product of the third side lengths of each triangle, which is By substitution, we see that . We also know . Since we want , multiplying both sides by get us . Now squaring gives .
In with a right angle at , point lies in the interior of and point lies in the interior of so that , , and the ratio . What is the ratio ? (2019 AMC 10B Problem, Question#16)
- A.
- B.
- C.
- D.
- E.
Without loss of generality, let and .
Let and . As and are isosceles, and , Then , so is a triang|e with .
Then , and is a triangle.
In isosceles triangles and , drop altitudes from and onto ; denote the feet of these altitudes by and respectively. Then by similarity, so we get that , and , Similarly we get , and .
Let , and . (For this solution, is above , and is to the right of ). Also let , so , which implies .
Similarly, , which implies . This further implies that
Now we see
that .
Thus is a right triangle, with side lengths of , , and (by the Pythagorean Theorem, or simply the Pythagorean triple ). Therefore (by definition),,
and , Hence (by the double angle fomua),
giving ,
By the Law of Cosines in , if , we have
,
Now .
Thus the answer is .
Draw a nice big diagram and measure. The answers to this problem are not very close, so it is quite easy to get to the correct answer by simply drawing a diagram.(Note: this strategy should only be used as a last resort).
A red ball and a green ball are randomly and independently tossed into bins numbered with positive integers so that for each ball, the probability that it is tossed into bin is for , , , What is the probability that the red ball is tossed into a highernumbered bin than the green ball? (2019 AMC 10B Problem, Question#17)
- A.
- B.
- C.
- D.
- E.
By symmetry, the probability of the red ball landing in a highernumbered bin is the same as the probability of the green ball landing in a highernumbered bin.Clearly, the probability of both landing in the same bin is (by the geometric series sumformua). Therefore the other two probabilites have to both be .
Suppose the green ball goes in bin , for some . The probability of this occuring is . Given that this occurs, the probability that the red ball goes in a highernumbered bin is (by the geometric series sum formula). Thus the probability that the green ball goes in bin , and the red ball goes in a bin greater than , is . Summing from to infinity, we get . where we again used the geometric series sum formula. (Alternatively, if this sum equals , then by writing out the terms and multiplying both sides by4, we see , which give ).
The probability that the two balls will go into adjacent bins is by the geometric series sum formula. Similarly, the probability that the two balls will go into bins that have a distance of from each other is (again recognizing a geometric series). We can see that each time we add a bin between the two balls. the probability halves. Thus, our answer is , which, by the geometric series sum formula, is .
Define a win as a ball appearing in higher numbered box.
Start from the first box.
There are possible results in the box: Red, Green, Red and Green, or none with an equal probablly of for each. if none of the balls is in the first box, the game restarts at the second box with the same kind of probaility distribution, so if is the probability that Red wins, we we can write ; there is a probabilty that "Red” wins immediately, a probability in the cases ”Geen” or “Red and Green”, and in the ”None" case (which occurs with probability), we then start again, giving the same probability . Hence,solving the equation, we get .
Write out the infinite geometric series as , ,, , To find the probablilty that red goes in a highernumbered bin than green, we can simply remove all odd-index terms(i.e term , term , etc.), and then sum the remaining termsthis is in fact precisely equivalent to the method of Solution .
Writing this out as another infinite geometric sequence, we are left with , , , Summing, we .
Henry decides one morning to do a workout, and he walks of the way from his home to his gym. The gym is kilometers away from Henry's home. At that point, he changes his mind and walks of the way from where he is back toward home.When he reaches that point, he changes his mind again and walks of the distance from there back toward the gym. If Henry keeps changing his mind when he has walked of the distance toward either the gym or home from the point where he last changed his mind, he will get very close to walking back and forth between a point kilometers from home and a point kiometers from home. What is ? (2019 AMC 10B Problem, Question#18)
- A.
- B.
- C.
- D.
- E.
Let the two points that Henry walks in between be and , with being closer to home. As given in the problem statement, the distances of the points and from his home are and respectively.
By symmetry, the distance of point from the gym is the same as the distance from home to point .
Thus, . In addition, when he walks from point to home, he walks of the distance,
ending at point . Therefore, we know that . By subsituting, we
get . Adding these equations now gives .
Multipiying by , we get , so .
We assume that Henry is walking back and forth exactly between points and , with closer to Henry’s home than . Denote Henry’s home as a point and the gym as a point .
Then and , so .
Therefore, .
Let be the set of all positive integer divisors of . How many numbers are the product of two distinct elements of ? (2019 AMC 10B Problem, Question#19)
- A.
- B.
- C.
- D.
- E.
Divide the circle into four parts: the top semicircle ; the bottom sector , whose arc angle is because the large circle's radius is and the short length(the radius of the smaller semicircles) is , giving a triangle; the triangle formed by the radii of and the chord , and the four parts which are the corners of a circle inscribed in a square , Then the area is (in , we find the area of the shaded region above the semicircles but below the diameter, and in we find the area of the bottom shaded region).
The area of is ,
The area of is .
For the ara of , th. radius of , and he distance of (the smaller semicicles' radius ) to .
creates two triangles, so s area is ,
The area of is ,
Hence, finding . the desired areas is , so the answer is .
As shown in the figure, line segment trisected by points and so that .Three semicircles of radius , , and , have their diameters on , and are tangent to line at , , and , respectively. A circle of radius has its center on . The area of the region inside the circle but outside the three semicircles, shaded in the figure, can be expressed in the form , where , , , and are positive integers and and are relatively prime. What is ? (2019 AMC 10B Problem, Question#20)
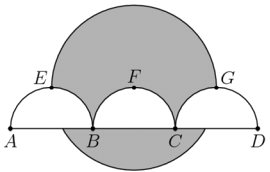
- A.
- B.
- C.
- D.
- E.
Divide the circle into four parts: the top semicircle ; the bottom sector , whose arc angle is because the large circle's radius is and the short length(the radius of the smaller semicircles) is , giving a triangle; the triangle formed by the radii of and the chord , and the four parts which are the corners of a circle inscribed in a square , Then the area is (in , we find the area of the shaded region above the semicircles but below the diameter, and in we find the area of the bottom shaded region).
The area of is ,
The area of is .
For the area of , the radius of , and the distance of (the smaller semicicles' radius ) to .
creates two triangles, so s area is .
The area of is ,
Hence, finding . the desired area is , so the answer is .
Debra flips a fair coin repeatedly, keeping track of how many heads and how many tails she has seen in total, until she gets either two heads in a row or two tails in a row, at which point she stops flipping. What is the probability that she gets two heads in a row but she sees a second tail before she sees a second head? (2019 AMC 10B Problem, Question#21)
- A.
- B.
- C.
- D.
- E.
We firstly want to find out which sequences of coin flips satisfy the given condition. For Debra to see the second tail before the seecond head, her first flip can't be heads, as that would mean she would either end with double tails before seeing the second head, or would see two heads before she sees two tails. Therefore, her first flip must be tails. The shortest sequence of flips by which she can get two heads in a row and see the second tail before she sees the second head is , which has a probability of . Furthemore, she can prolong her coin fliping by adding an extra , which itself has a probability of . Since she can do this indefinitely, this gives an infinite geometric series, which means the answer (by the geometic series sum formula) is .
Note that the sequence must start in , which happens with probability. Now, let be the probability that Debra will get two heads in a row after flipping . Either Debra flips two heads in a row immediately (probability ), or flips a head and then a tail and reverts back to the"original position”(probability ). Therefore, , so , so our final answer is .
Raashan, Sylvia, and Ted play the following game. Each starts with $. A bell rings every seconds, at which time each of the players who currently have money simultaneously chooses one of the other two players independently and at random and gives $ to that player. What is the probability that after the bell has rung times, each player will have $?(For example, Raashan and Ted may each decide to give $ to Sylvia, and Sylvia may decide to give her her dollar to Ted, at which point Raashan will have $, Sylvia will have $, and Ted will have $, and that is the end of the first round of play. In the second round Rashaan has no money to give, but Sylvia and Ted might choose each other to give their $ to, and the holdings will be the same at the end of the second round.)(2019 AMC 10B Problem, Question#22)
- A.
- B.
- C.
- D.
- E.
On the first turn, each player starts off with $. Each turn after that, there are only two possibilies:
either everyone stays at $, which we will write as , or the distribution of money becomes $$$ in some order, which we write as .We will consider these two states separately,
In the state, each person has two choices for whom to give their dollar to, meaning there are possible ways that the money can be rearranged. Note that there are only two ways that we can reach again:
.Raashan gives his money to Sylvia, who gives her money to Ted, who gives his money to Raashan.
.Raashan gives his money to Ted, who gives his money to Sylvia, who gives her money to Raashan.
Thus, the probablity of staying in the state is , while the probability of going to the state is (we can check that the other posibiiies lead to .
In the state, we will label the person with $ as person , the person with $ as person , and the person with $ as person . Person has two options for whom to give money to, and person has options for whom to give money to, meaning there are total ways the money can be redistributed. The only way that the distrbution can return to is if gives $ to , and gives $ to . We check the other possibilies to find that they all lead back to . Thus, he probability of going to the state is , while the probability of staying in the state is .
No matter which state we are in, the probability of going to the state is always . This means that, after the bell rings times, regardless of what state the money distribution is in, there is a probability of going to the state after the bell ring. Thus, our answer is simply .
Points and lie on circle in the plane. Suppose that the tangent lines to at and intersect at a point on the axis. What is the area of ? (2019 AMC 10B Problem, Question#23)
- A.
- B.
- C.
- D.
- E.
First, observe that the two tangent lines are of identical length. Therefore, supposing that the point of intersection is , the Pythagorean Theorem gives .
Further, notice (due to the right angles formed by a radius and its tangent line) that the quadrilateral (a kite) defined by the circle's center,, , and is cyclic. Therefore, we can apply Ptolemy's Theorem to give , where is the distance between the circle's center and . Therefore, . Using the Pythagorean Theorem on the triangle formed by the point , either one of or , and the circle's center, we find that , so , and thus the answer is .
We firstly obtain as in Solution . Label the point as . The midpoint of segment is . Notice that the center of the circle must lie on the line passing through the points and . Thus, the center of the circle lies on the line . Line is . Therefore, the slope of the line perpendicular to is , so its equation is .
But notice that this line must pass through and .
Hence . So the center of the circle is .
Finally, the distance between the center, , and point is . Thus the area of the circle is .
The midpoint of is . Let the tangent lines at and intersect at on the axis. Then is the perpendicular bisector of . . Let the center of the circle be . Then is similar to , so . The slope of is , so the slope of is . Hence, the equation of is . Letting , we have , so ..
Now, we compute , , and .
Therefore , and consequently, the area of the circle is .
Firstly, the point of intersection of the two tangent lines has an equal distance to points and due to power of a point theorem. This means we can easily find the point, which is . Label this point . is an isosceles triangle with lengths, , , and . Label the midpoint of segment as . The height of this triangle, or , is .
Since bisects , contains the diameter of circle . Let the two points on circle where intersects be and with being the shorter of the two. Now let be and be . By Power of a Point on and , . Applying Power of a Point again on and , . Expanding while using the fact that , . Plugging this into , . Using the quadratic formula, , and since , . Since this is the diameter, the radius of circle is , and so the area of circle is frac {85}{8}\pi$$.
Define a sequence recursively by and
for all nonnegative integers . Let be the least positive integer such that
.
In which of the following intervals does lie?
(2019 AMC 10B Problem, Question#24)
- A.
- B.
- C.
- D.
- E.
We first prove that for all , by induction. Observe that
so (since is clearly positive for all , from the initial definition), if and only if .
We similarly prove that is decreasing, since
Now we need to estimate the value of , which we can do using the rearranged equation
Since is decreasing, is clearly also decreasing, so we
have and
This becomes The problem thus reduces to finding the least value of such that and
Taking logarithms, we get and , i.e. and .
As approximations, we can use , , and . These allow us to estimate that which gives the answer as .
The condition where gives the motivation to make a substitution to change the equilibrium from to . We can substitute to achieve that.
Now, we need to find the smallest value of such that given that and the recursion .
Using wishful thinking, we can simplify the recursion as follows:
The recursion looks like a geometric sequence with the ratio changing slightly after each term. Notice from the recursion that the sequence is strictly decreasing, so all the terms after will be less than . Also, notice that all the terms in sequence will be positive. Both of these can be proven by induction. With both of those observations in mind, . Combining this with the fact that the recursion resembles a geometric sequence, we conclude that . is approximately equal to and the ranges that the answer choices give us are generous, so we should use either or to find a rough estimate for . is , while is close to because is , which is close to .
Therefore, we can estimate that . Putting both sides to the power, we get But , so and therefore, . This tells us that is somewhere around , so our answer is .
How many sequences of and of length are there that begin with a , end with a , contain no two consecutive , and contain no three consecutive ? (2019 AMC 10B Problem, Question#25)
- A.
- B.
- C.
- D.
- E.
We can deduce, from the given restrictions, that any valid sequence of length will start with a followed by either or . Thus we can define a recursive function , where is the number of valid sequences of length . This is because for any valid sequence of length , you can append either or and the resulting sequence will still satisfy the given conditions. It is easy to find and by hand, and then by the recursive formula, we have .
After any particular , the next in the sequence must appear exactly or positions down the line. In this case, we start at position and end at position , i.e. we move a total of positions down the line. Therefore, we must add a series of and to get . There are a number of ways to do this:
Case 1: nine - there is only way to arrange them.
Case 2: two and six - there are ways to arrange them.
Case 3: four and three - there are ways to arrange them.
Case 4: six - there is only way to arrange them. Summing the four cases gives .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
