AMC 10 Daily Practice - Probability

Complete problem set with solutions and individual problem pages

Problem 1 Easy

If five students, A, B, C, D and E, stand in a row to take pictures. The probability that A and B are adjacent is            .

  • A.

    \frac{4}{5}

  • B.

    \frac{3}{5}

  • C.

    \frac{2}{5}

  • D.

    \frac{1}{5}

Answer:C

P=\frac{{_4P_4} \cdot {_2P_2}}{{_5P_5}}=\frac{2}{5}.

Link Problem
Problem 2 Easy

Two teachers and two students are lined up in a row for a photo. Let A be the number of teachers between the two students. Then E(A)=            .

  • A.

    \frac{1}{4}

  • B.

    \frac{1}{3}

  • C.

    \frac{2}{3}

  • D.

    \frac{4}{3}

  • E.

    \frac{3}{4}

Answer:C

The possible values of the random variable A are 0,1, and 2.

\begin{aligned} & P(A=0)=\frac{2 \times 2+2 \times 2 \times 2}{A_4^4}=\frac{1}{2} \\ & P(A=1)=\frac{C_2^1 \cdot A_2^2 \cdot C_2^1}{A_4^4}=\frac{1}{3} \\ & P(A=2)=\frac{2 \times 2}{A_4^4}=\frac{1}{6} \end{aligned}

Therefore,

E(A)=0 \times \frac{1}{2}+1 \times \frac{1}{3}+2 \times \frac{1}{6}=\frac{2}{3}.

Link Problem
Problem 3 Easy

Sonya the frog chooses a point uniformly at random lying within the square\left[ 0,6\right]\times\left[ 0,6\right] in the coordinate plane and hops to that point. She then chooses a distance uniformly at random in the interval [0, 1] and a direction uniformly at random from {north, east, south, west}. All her choices are independent. She now hops the chosen distance in the chosen direction. What is the probability that she lands outside the square? (2023 AMC 10B Problems, Question #19)

  • A.

    \frac{1}{6}

  • B.

    \frac{1}{12}

  • C.

    \frac{1}{4}

  • D.

    \frac{1}{10}

  • E.

    \frac{1}{9}

Answer:B

WLOG, we assume Sonya jumps 0.5 units every time, since that is her expected value.

If Sonya is within 0.5 blocks of an edge, she can jump off the board. Let us examine the region that is at most 0.5 blocks from exactly one edge.

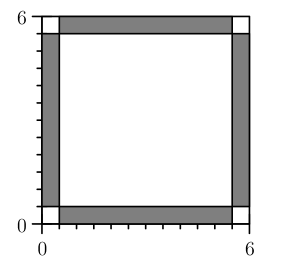
If Sonya starts in this region, she has a \dfrac14 chance of landing outside (there's exactly one direction she can hop to get out). The total area of this region is 4\cdot0.5\cdot5=10. For this region, Sonya has a \dfrac14 chance, so we multiply 10 by \dfrac14 to get 2.5.

If Sonya is in one of the corner squares, she can go two directions to get out, so she has a \dfrac24=\dfrac12 chance to get out. The total area is 0.5\cdot0.5\cdot4=1, so this region yields \dfrac12\cdot1=\dfrac12.

Adding the two, we get 3. This is out of 36 square units of area, so our answer is thus \boxed{\textbf{(B) }\tfrac{1}{12}}.

Link Problem
Related Paper
2017 AMC 10 A 2017 AMC 10 B AMC 10 Daily Practice - Counting AMC 10 Daily Practice - Diophantine Equations
Table of Contents
  • 1
  • 2
  • 3
Think Academy Powered by ChatGPT