AMC 10 Daily Practice - Polygons

Complete problem set with solutions and individual problem pages

Problem 1 Easy

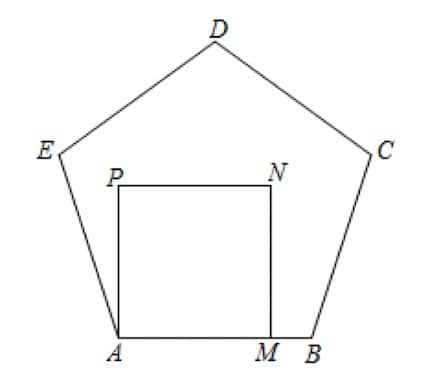
As shown in the diagram, the side AM of the square AMNP lies on the side AB of the regular pentagon ABCDE, what is the measure of \angle PAE?

  • A.

    15^\circ

  • B.

    16^\circ

  • C.

    17^\circ

  • D.

    18^\circ

  • E.

    19^\circ

Answer:D

\because quadrilateral A M N P is a square, pentagon A B C D E is regular, \therefore \angle E A B=\frac{(5-2) \times 180^{\circ}}{5}=108^{\circ}, \angle P A B=90^{\circ},

\therefore \angle P A E=\angle E A B-\angle P A B=18^{\circ}, si the answer is 18^\circ.

Link Problem
Problem 2 Easy

Given that the distance from the center of a regular dodecagon (12-sided polygon) to one of its vertices is 45, and the internal blank area is composed of squares and triangles, the area of the shaded region is            .

  • A.

    2000

  • B.

    2010

  • C.

    2015

  • D.

    2025

  • E.

    2030

Answer:D

Solution 1:

r=45^\circ

x^2 = 45^2 + 45^2 - 2 \cdot 45 \cdot 45 -\frac{\sqrt3}{2} = 2 \cdot 45^2 - 45^2\cdot \sqrt{3}

A = 12 \cdot \frac{1}{2} \cdot 45 \cdot 45 \cdot \frac{1}{2}

= 3 \cdot 45^2

A_\triangle = \frac{\sqrt{3}}{4} \cdot x^2 = \frac{\sqrt{3}}{4} (2 \cdot 45^2 - 45^2\cdot \sqrt{3})

8A_\triangle = 2\sqrt{3} (2 \cdot 45^2 - 45^2\cdot \sqrt{3})

4A_\square = 8 \cdot 45^2 - 4\cdot 45^2\sqrt{3}

8A_\triangle = 4\sqrt{3} \cdot 45^2 - 6 \cdot 45^2

4A_\square + 8A_\triangle = 2 \cdot 45^2

A = 45^2 = 2025

[Note: x represent the side length of dodecagon]

Solution 2:

(x + \frac{\sqrt{3}}{2}x)^2 + (\frac{x}{2})^2 = 45^2

x^2 + \frac{3}{4}x^2 + \sqrt{3}x^2 + \frac{x^2}{4} = 45^2

(2+\sqrt{3})x^2 = 45^2

x^2 = \frac{45^2}{2 + \sqrt{3}}

\frac{1}{2}x(\frac{\sqrt{3}}{2}x+x) = \frac{\sqrt{3} + 2}{4} x^2

A = 12 \cdot \frac{\sqrt{3} + 2}{4}x^2

= 3(\sqrt{3} + 2) \cdot \frac{45^2}{2 + \sqrt{3}}

= 3 \cdot 45^2

A_\triangle = \frac{\sqrt{3}}{4}x^2 \cdot 8

= \frac{\sqrt{3}}{4} \cdot \frac{45^2}{2 + \sqrt{3}} \cdot 8

= \frac{2\sqrt{3} \cdot 45^2}{2 + \sqrt{3}}

A_\square = x^2 \cdot 4

= \frac{4 \cdot 45^2}{2 + \sqrt{3}}

A_{\triangle + \square} = \frac{2\sqrt{3} \cdot 45^2 + 4 \cdot 45^2}{2 + \sqrt{3}}

= \frac{2 \cdot 45^2 \cdot (\sqrt{3} + 2)}{2 + \sqrt{3}}

= 2 \cdot 45^2

A_{shaded} = 3 \cdot 45^2 - 2\cdot 45^2

= 45^2

= 2023

[Note: x represent the side length of dodecagon]

Link Problem
Problem 3 Easy

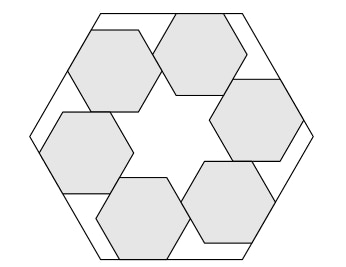
Six regular hexagonal blocks of side length 1 unit are arranged inside a regular hexagonal frame. Each block lies along an inside edge of the frame and is aligned with two other blocks, as shown in the figure below. The distance from any corner of the frame to the nearest vertex of a block is \frac{3}{7} unit. What is the area of the region inside the frame not occupied by the blocks? (2023 AMC 10A problems, Question #24)

 

  • A.

    \frac{13 \sqrt{3}}{3}

  • B.

    \frac{216 \sqrt{3}}{49}

  • C.

    \frac{9 \sqrt{3}}{2}

  • D.

    \frac{14 \sqrt{3}}{3}

  • E.

    \frac{243 \sqrt{3}}{49}

Answer:C

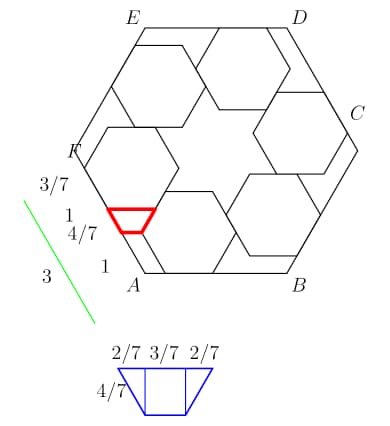
Examining the red isosceles trapezoid with 1 and \dfrac{3}{7} as two bases, we know that the side lengths are \dfrac{4}{7} from 30-60-90 triangle.

 

We can conclude that the big hexagon has side length 3.

 

Thus the target area is: area of the big hexagon - 6 * area of the small hexagon. \dfrac{3\sqrt{3}}{2}(3^2-6\cdot1^2) = \dfrac{3\sqrt{3}}{2}(3) = \boxed{\textbf{(C)}~\frac{9 \sqrt{3}}{2}}

Link Problem
Related Paper
AMC 10 Daily Practice - Diophantine Equations AMC 10 Daily Practice - Modular Arithmetic AMC 10 Daily Practice - Tangency AMC 10 Daily Practice - Similarity
Table of Contents
  • 1
  • 2
  • 3
Think Academy Powered by ChatGPT