AMC 10 Daily Practice - Similarity
Complete problem set with solutions and individual problem pages
In the figure, . If , , , then .
- A.
- B.
- C.
- D.
- E.
∵,,
∴,
∵,
∴,
∴,
∵,,,
∴,
∴
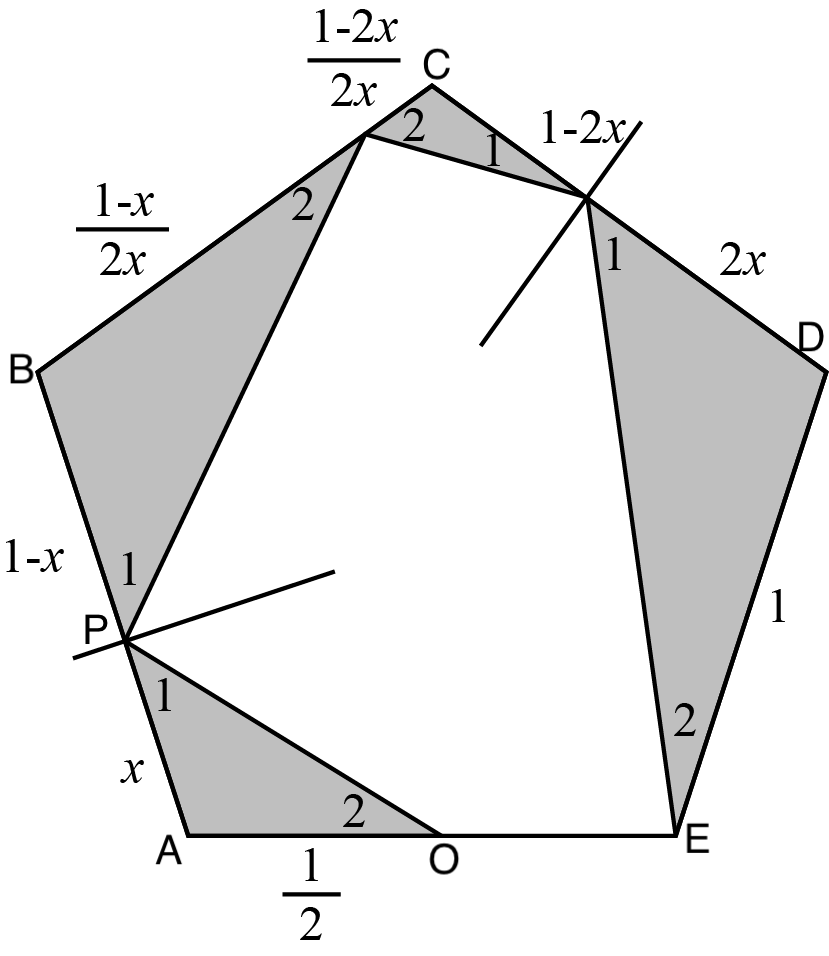
In a new billiard game, the table is a regular pentagon with side length meter. The five vertices are pockets. The ball is always struck from the midpoint of . When the ball hits the edge of the table, it rebounds. If the ball reaches a pocket, it falls in. After a shot, the ball first hits point on edge , then rebounds towards edge , rebounds again at edge , then rebounds at edge , and finally falls into pocket . What is the distance between point and point ?
- A.
- B.
- C.
- D.
- E.
By symmetry, we know all are equal and all are equal. So the triangles are all similar.
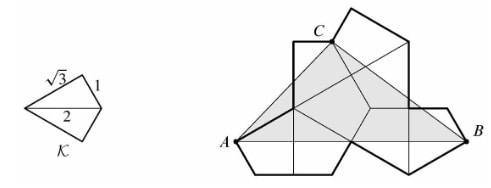
Let be the kite formed by joining two right triangles with legs and along a common hypotenuse. Eight copies of are used to form the polygon shown below. What is the area of triangle ? (2024 AMC 10A Problems, Question #22)
- A.
- B.
- C.
- D.
- E.
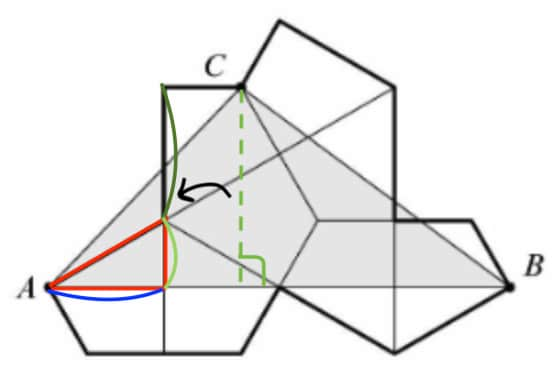
First, we should find the length of . In order to do this, as we see in the diagram, it can be split into 4 equal sections. Since diagram shows us that it is made up of two triangles, then the triangle outlined in red must be a triangle, as , and the two lines are perpendicular (it is proveable, but during competition, it is best to assume this is true, as the diagram is draw pretty well to scale). Also, since we know the length of the longest side of the red triangle is , then the side we are looking for, which is outlined in blue, must be by the relationship of triangles. Therefore , which is the base of the triangle we are looking, for must be
Now all we have to do is find the height. We can split the height into 2 sections, the green and the light green. The green section must be , as shows us. Also, the light green section must be equal to , as in the previous paragraph, the triangle outlined in red is . Then, the green section, which is the height, must be , which is just .
Then the area of the triangle must be , which is just
- 1
- 2
- 3
