AMC 10 Daily Practice - Similarity

Complete problem set with solutions and individual problem pages

Problem 1 Easy

In the figure, DE{//}BC. If BD=12, AD=2, AE=3, then AC=            .

  • A.

    6

  • B.

    12

  • C.

    9

  • D.

    15

  • E.

    18

Answer:D

∵BD=12，AD=2,

∴AB=BD-AD=12-2=10,

∵BC{//}DE,

∴\triangle BCA\mathbf{\backsim }\triangle DEA,

∴\frac{AC}{AE}=\frac{BA}{DA},

∵AE=3，AB=10，AD=2,

∴\frac{AC}{3}=\frac{10}{2},

∴AC=15

Link Problem
Problem 2 Easy

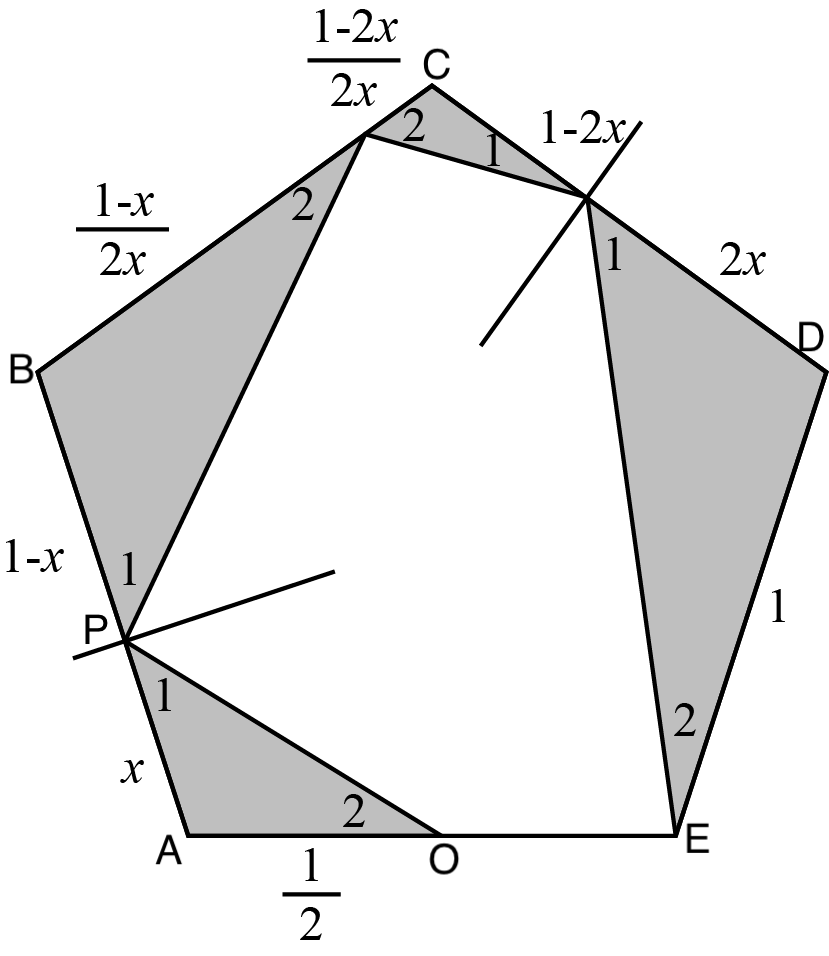
In a new billiard game, the table is a regular pentagon ABCDE with side length 1 meter. The five vertices are pockets. The ball is always struck from the midpoint O of AE. When the ball hits the edge of the table, it rebounds. If the ball reaches a pocket, it falls in. After a shot, the ball first hits point P on edge AB, then rebounds towards edge \overline{BC}, rebounds again at edge \overline{BC}, then rebounds at edge \overline{CD}, and finally falls into pocket E. What is the distance between point P and point A?

​​​

  • A.

    \frac{1}{5}

  • B.

    \frac{1}{6}

  • C.

    \frac{2}{5}

  • D.

    \frac{3}{4}

  • E.

    \frac{5}{2}

Answer:C

By symmetry, we know all \angle 1 are equal and all \angle 2 are equal. So the triangles are all similar.

\frac{1-2x}{2x} + \frac{1-x}{2x} = 1

2 - 3x = 2x

x = \frac{2}{5}

Link Problem
Problem 3 Easy

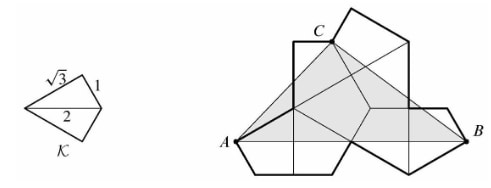
Let \mathcal K be the kite formed by joining two right triangles with legs 1 and \sqrt3 along a common hypotenuse. Eight copies of \mathcal K are used to form the polygon shown below. What is the area of triangle \triangle ABC? (2024 AMC 10A Problems, Question #22)

 

  • A.

    2+3\sqrt3

  • B.

    \frac{9}{2}\sqrt3

  • C.

    \dfrac{10+8\sqrt3}{3}

  • D.

    8

  • E.

    5\sqrt3

Answer:B

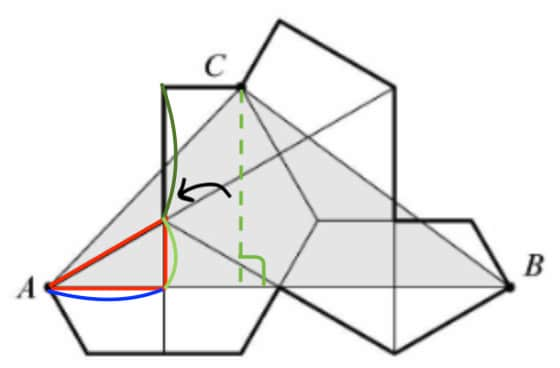
First, we should find the length of AB. In order to do this, as we see in the diagram, it can be split into 4 equal sections. Since diagram K shows us that it is made up of two {30,60,90} triangles, then the triangle outlined in red must be a 30,60,90 triangle, as {30+30=60}, and the two lines are perpendicular (it is proveable, but during competition, it is best to assume this is true, as the diagram is draw pretty well to scale). Also, since we know the length of the longest side of the red triangle is {\sqrt3}, then the side we are looking for, which is outlined in blue, must be \frac{3}{2} by the {1,\sqrt3, 2} relationship of {30,60,90} triangles. Therefore AB, which is the base of the triangle we are looking, for must be 6.

 

 

Now all we have to do is find the height. We can split the height into 2 sections, the green and the light green. The green section must be {\sqrt3}, as K shows us. Also, the light green section must be equal to {\frac{\sqrt3}{2}}, as in the previous paragraph, the triangle outlined in red is 30,60,90. Then, the green section, which is the height, must be {\sqrt3}+{\frac{\sqrt3}{2}}, which is just {\frac{3\sqrt3}{2}}.

 

 

Then the area of the triangle must be {\frac{1}{2}}\cdot {b} \cdot {h}, which is just \boxed{ \textbf{(B) } \frac{9}{2} \sqrt3}.

Link Problem
Related Paper
AMC 10 Daily Practice - Polygons AMC 10 Daily Practice - Tangency AMC 10 Daily Practice - Polynomial Functions AMC 10 Daily Practice - Sequences
Table of Contents
  • 1
  • 2
  • 3
Think Academy Powered by ChatGPT