AMC 10 Daily Practice Round 4
Complete problem set with solutions and individual problem pages
Define for all real numbers and . Find the value of .
- A.
- B.
- C.
- D.
- E.
※,
※.
∴ ※(※).
Real numbers ,, and satisfy the inequalities ,, and . Which of the following numbers is necessarily positive?
- A.
- B.
- C.
- D.
- E.
Notice that must be positive because . Therefore the answer is .
The other choices:
As grows closer to , decreases and thus becomes less than .
can be as small as possible , so grows close to as approaches .
For all , , and thus it is always negative.
The same logic as above, but when this time.
Jason walks from his home to school. If he walks meters per minute, he will be minutes late; if he walks meters per minute, he will be minutes late. In order to arrive on time, how fast should Jason walk in meters per minute?
- A.
- B.
- C.
- D.
- E.
The required time is minutes. meters per minute. Alternatively, we can also set up a rational equation to solve the problem.
A rectangle has and . Points and lie on sides and , respectively, such that and the area of is . What is ?
- A.
- B.
- C.
- D.
- E.
Since the area of is , we get that . Thus, . Let . Then and , so . Expanding and factoring gives , so either or .
If , then and , which is impossible, so thus . This gives and . Since is a rectangle, , so applying the Pythagorean Theorem on gives . Thus, .
In the coordinate system, the and coordinates of the intersection point between lines and are both integers. How many possible values of are there?
- A.
- B.
- C.
- D.
- E.
Construct the system .
Plug the first equation into the second equation, we have .
It is clear that , so we have .
When or , is an integer, and now is also an integer.
Therefore, , four of them.
A bicycle has two wheels, while a tricycle has three wheels. There are a such vehicles with wheels. Find the number of bicycles.
- A.
- B.
- C.
- D.
- E.
Suppose that all vehicles are tricycles, then there are bicycles. Alternatively, we can also set up system of linear equations to solve the problem.
Two squares of side lengths and lie within a third square of side length , as shown below. What is the area of the shaded region?
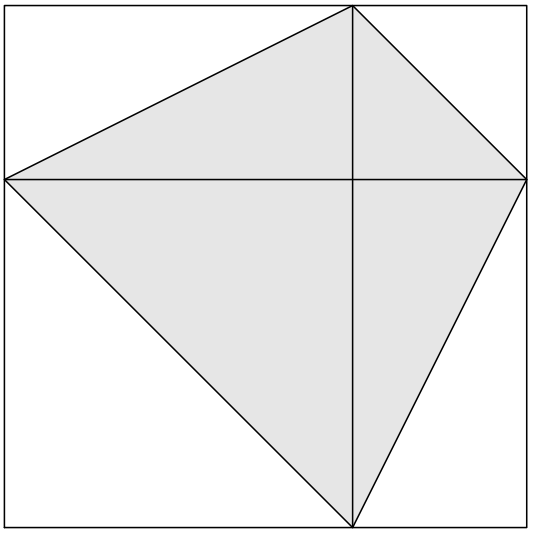
- A.
- B.
- C.
- D.
- E.
Each of the shaded triangles can be paired with a congruent but unshaded triangle, and vice versa. Hence, the shaded region and the combined unshaded regions have the same area, so the shaded region has half the area of the entire square. The requested answer is therefore .
Which of the following numbers is a perfect square?
- A.
- B.
- C.
- D.
- E.
Note that for all positive , we have .
We must find a value of such that is a perfect square. Since is a perfect square, we must also have be a perfect square. In order for to be a perfect square, must be twice a perfect square. From the answer choices, works, thus, and our desired answer is .
Cards labeled from to are distributed to students A, B, and C, three cards each person without repetition. The following are the conversations between the students.
A: The three numbers on my cards form an arithmetic sequence.
B: Me too.
C: Only my cards do not form an arithmetic sequence.
Suppose that everyone is telling the truth, find the minimum of the sum of the numbers in three cards of C.
- A.
- B.
- C.
- D.
- E.
As the numbers of A and B form arithmetic sequences, their sums must be multiples of . The sum of cards is , which is also a multiple of . Therefore, the sum of C is also a multiple of . The sum of C can not be , so the sum is at least . Check and find is the correct answer.
A:
B:
C:
Let be a convex quadrilateral such that and. Let be the intersection of the diagonals and . If , find the area of .
- A.
- B.
- C.
- D.
- E.
Construct .
∵ , ,
∴ .
∵ ,
∴ , ,
∵ ,
∴ ,
∵ , ,
∴ ,
∴ , or , ,
∴ ,
,
∴ .
Therefore, .
A palindrome is a number that has the same value when read from left to right or from right to left. (For example, is a palindrome.) Determine the number of palindromes between and .
- A.
- B.
- C.
- D.
- E.
Enumerate based on patterns: , , , , , , , , , , .
Consider the Fibonacci Sequence , , , , , , . Starting the third number, each succeeding number is the sum of the previous two numbers. Among the first numbers in the sequence, how many of them are multiples of ?
- A.
- B.
- C.
- D.
- E.
We can determine the pattern of remainders when each term in the sequence is divided by : , , , , , , , , , , , , , , , , , , , , , , , , . We find that a remainder of appears once for every numbers if the divisor is . As , there are such numbers.
Consider positive integers such that , which of the following is a possible value of ?
- A.
- B.
- C.
- D.
- E.
None of the above
Since , , and are both prime and .
Let , , , , , , , ,
Then ,
So we are good as long as is not prime.
For example, .
This is true when , , , .
Circles , , and each have radius . Circles and share one point of tangency. Circle has a point of tangency with the midpoint of . One side of rectangle is tangent to both circles and , and its opposite side is tangent to circle . The other two sides are tangent to circles and , respectively. What is the area of the part that is inside the rectangle but not inside the circle?
- A.
- B.
- C.
- D.
- E.
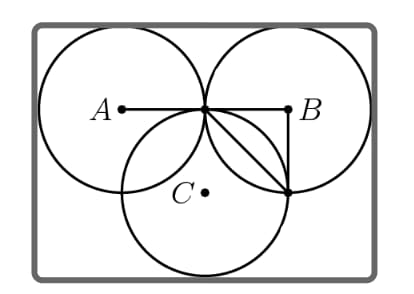
By the principle of inclusion-exclusion, it can be deduced that the desired area is equal to the area of the rectangle minus the sum of the areas of the three circles , and , plus the overlapping area between circle and circles and .
Then, we can compute the shaded area as the area of half of plus the area of the rectangle minus the area of the two sectors created by and . This is .
The area of the rectangle is , so the area is .
In the figure, a semicircle with diameter intersects each side of rectangle at exactly one point. The lengths of segments and are centimeters and centimeters, respectively. The area of the shaded region is square centimeters. Find the value of . (Assuming the value of is .)
- A.
- B.
- C.
- D.
- E.
Let be a line segment with midpoint . Draw a perpendicular line from to at point . Connect and .
Then, is perpendicular to , and is perpendicular to . Given that has a length of , we can deduce that . Therefore, can be calculated as .
The length of is , and since bisects , we have . Consequently, .
The length of is given as .
Now, we want to find the area of the shaded region, denoted as . This can be obtained by subtracting the area of the semicircle from the area of quadrilateral . The area of quadrilateral can be calculated as . The area of the semicircle can be calculated as , where the radius is . Thus, the area of the shaded region is:
Therefore, the answer is .
Let be a real number. If , what is the simplified value of ?
- A.
- B.
- C.
- D.
- E.
Given , we can deduce that (since the absolute value of a number is non-negative, and here it equals the negative value of ).
Now, let's simplify the expression :
.
Hence, the simplified value of the expression is .
The correct answer is .
Bertha has daughters and no sons. Some of her daughters have daughters, and the rest have none. Bertha has a total of daughters and granddaughters, and no great-granddaughters. How many of Bertha's daughters and grand-daughters have no children? (2004 AMC 10A Problems, Problem #6)
- A.
- B.
- C.
- D.
- E.
Solution 1: Since Bertha has daughters, she has granddaughters, of which none have daughters. Of Bertha's daughters, have daughters, so do not have daughters. Therefore, of Bertha's daughters and granddaughters, do not have daughters. .
Solution 2: Bertha has granddaughters, none of whom have any daughters. The granddaughters are the children of of Bertha's daughters, so the number of women having no daughters is .
Draw a tree diagram and see that the answer can be found in the sum of granddaughters, daughters, and more daughters. Adding them together gives the answer of .
In the figure, the area of triangle is . Connecting the points that divide segments and into five equal parts, what is the area of the shaded region in the figure?
- A.
- B.
- C.
- D.
- E.
The areas of the shaded regions in the figure have a ratio of from top to bottom. To find the area of the shaded region, we sum up the areas of the three shaded regions from top to bottom, which correspond to the areas with ratios . Then, we divide this sum by the total sum of all the areas (which corresponds to the total sum of the ratios in the figure).
The shaded region's area is .
Hence, the area of the shaded region is .
In rectangle , . Point lies on side , and segments and trisect . What is the perimeter of ?
- A.
- B.
- C.
- D.
- E.
Since is trisected, . Thus, , , and Adding them, we get .
In a candy distribution scenario, three individuals, A, B, and C, each have a positive integer number of candies. If A gives B candies, B's candy count will be twice the sum of A and C's candy counts. If A gives C candies, C's candy count will be three times the sum of A and B's candy counts. How many candies do A, B, and C have in total?
- A.
- B.
- C.
- D.
- E.
Let , , and represent the numbers of candies for A, B, and C, respectively. From the given conditions, we have the following system of equations:
Solving and simplifying, we get:
From equation , we have . Substituting this into equation , we get:
Hence, . Since and are positive integers, we have:
Therefore, . After checking, we find that satisfies the equation, and this implies that . Thus, and .
So, the number of candies for A, B, and C respectively are:
candies candies candies
The total number of candies for A, B, and C is .
Therefore, the answer is .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
