AMC 10 Daily Practice Round 3
Complete problem set with solutions and individual problem pages
Mei can travel to her grandma's house by a direct route, or by a scenic route that is longer. When she travels by the scenic route, and comes directly home, the round trip is . How long is the direct route?
- A.
- B.
- C.
- D.
- E.
Let the length of the direct route be kilometers, so the length of the scenic route is kilometers. When Mei chooses the scenic route to her grandmother's house and then directly returns home, the total round trip includes the scenic route on the way there and the direct route on the way back. Therefore, the total length can be represented as: . Solve this equation, . So, the length of the direct route is kilometers.
A flower bouquet contains pink roses, red roses, pink carnations, and red carnations. One third of the pink flowers are roses, three fourths of the red flowers are carnations, and six tenths of the flowers are pink. What percent of the flowers are carnations?
- A.
- B.
- C.
- D.
- E.
Let the total amount of flowers be . Thus, the number of pink flowers is , and the number of red flowers is . The number of pink carnations is and the number of red carnations is . Summing these, the total number of carnations is . Dividing, we see that .
In isosceles with , point lies on such that . Given that is isosceles, what is the degree measure of ?
- A.
- B.
- C.
- D.
- E.
Since is isosceles with , we know that is an isosceles right triangle. This gives the measure of is in isosceles .
Ponce rolls a four-sided die (from to ), a six-sided die (from to ), and an eight-sided die (from to ), all of which are perfectly fair. What is the probability that all three dice show the same number?
- A.
- B.
- C.
- D.
- E.
The result of the -sided die does not matter. To match with the next two tosses, we have the probability be .
The lines with equations , , , and form a trapezoid with area . If , what is the value of ?
- A.
- B.
- C.
- D.
- E.
Let and be the points at which the line with equation intersects the lines with equations and , respectively. Also, suppose has coordinates and has coordinates . The trapezoid in the problem is , as shown.
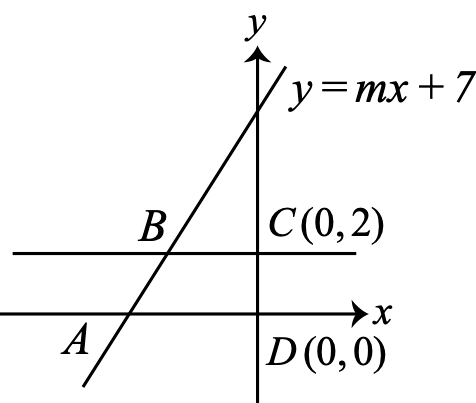
We can find the coordinates of and in terms of . To find the coordinates of , we find the point of intersection of the line with equation and the line with equation . Setting , we get . Note that the -coordinate of must be since it is, by definition, on the line with equation . Therefore, the coordinates of are . Similarly, the coordinates of are . Trapezoid has parallel bases and and height . The two bases are horizontal and have lengths and . The length of is . Therefore, the area of is . It is given that the area of the trapezoid is , so we have , or .
Exactly one of the five numbers shown below is not a divisor of Molly's favorite positive integer. Which one is it?
- A.
- B.
- C.
- D.
- E.
, while for the other four answer choices, none of which contains . Therefore, not necessarily divides Molly's favorite positive integer.
When two ants work together they can build an anthill in minutes. When the bigger ant works alone, an anthill can be built in minutes less than when the smaller ant works alone. How many minutes does it take the smaller ant to build an anthill when working alone?
- A.
- B.
- C.
- D.
- E.
Let be the number of minutes that it would take the bigger ant to build an anthill alone and let be the number of minutes that it would take the smaller ant to build an anthill alone. Since the bigger ant can build an anthill in minutes, the bigger ant builds anthills per minute. Likewise, the smaller ant can build anthills per minute. Thus, working together, the two ants build anthills per minute. It is also given that it takes the two ants minutes to build an anthill together, so this means they build anthills per minute working together. Hence, we get the equation . Multiplying this equation through by gives . From the other given condition, we get , so we can substitute to get . Expanding and rearranging, this equation becomes , which can be factored as . If , then , which does not make sense since must be positive. Therefore, .
Call a positive integer if all its digits are nonzero and it is divisible by each of its digits. How many two-digit positive integers are ?
- A.
- B.
- C.
- D.
- E.
Let be a two-digit good integer, where and are nonzero digits. Then, and must both divide . This implies divides and divides . Consider cases on the value of .
Case 1: . Then, the divisibility becomes divides . There are such digits , namely , , and .
Case 2: . Then, the divisibility becomes divides and divides . There are such digits , namely and .
Case 3: . Then, the divisibility becomes divides and divides . There are such digits , namely and .
Case 4: . Then, the divisibility becomes divides and divides . There are such digits , namely and .
Case 5: . Then, the only possible nonzero digit that is a multiple of is itself. Thus, . Then, is guaranteed to divide . Thus, there are good integers here. The total number of two-digit good integers is .
Sally arranges the numbers from to in a circle and then calculates the sum of each set of adjacent numbers. She would like an arrangement in which the smallest of these sums is as large as possible. If she chooses such an arrangement, what will this smallest sum be?
- A.
- B.
- C.
- D.
- E.
Let the smallest of the sums of three adjacent numbers be .
Then adding from the number around the circle and back to adds numbers in a row, so this value is at least .
However these numbers add to .
Hence so that and since is a whole number, .
Once it is known that has a chance of being the largest minimum, it is straightforward to find one of the many arrangements where all sums of adjacent numbers (shown in blue) are or more, such as the arrangement shown. This confirms that the smallest possible sum of adjacent numbers is .
Six identical equilateral triangles of side length are drawn outside a regular hexagon of side length , defining a larger hexagon as shown. What is the ratio of the area of the larger hexagon to the area of the smaller hexagon?
- A.
- B.
- C.
- D.
- E.
Each yelllow equilateral triangle can be divided in to unit equilateral triangles, for a total of unit equilateral triangles. The small regular hexagon counts unit equilateral triangles. Last, each white obtuse triangle is half of the area of a yellow equilateral trianlges, for a total of yellow equilateral traingles, or unit equilateral triangles.
The entire figure consists of unit equilateral triangles. Therefore, the required ratio is .
Triangle is equilateral with . Points and are on and points and are on such that both and are parallel to . Furthermore, triangle and trapezoids and all have the same perimeter. What is ?
- A.
- B.
- C.
- D.
- E.
Let , and . We want to find , which is nothing but .
Based on the fact that , , and have the same perimeters, we can say the following:
Simplifying, we can find that
Since , .
After substitution, we find that , and = .
Again substituting, we find = .
Therefore, = , which is .
A sequence of numbers , , , has its terms defined by for every integer . For example, . What is the largest positive integer for which the sum of the first terms (that is, is less than ?
- A.
- B.
- C.
- D.
- E.
Note that
This means that the sum of the first terms is less than exactly when is greater than .
As increases from 4 , each of and decreases, which means that their sum decreases as well. When .
When .
This means that is greater than exactly when and is less than when .
In other words, the sum of the first terms is less than for as well as for , which is the same as saying that this is true for .
Therefore, is the largest positive integer for which the sum of the first terms is less than .
A gold coin is worth more than a silver coin. The silver coin is worth less than the gold coin. Both and are positive integers. How many possible values for are there?
- A.
- B.
- C.
- D.
- E.
Let the values of a gold coin and a silver coin be and dollars, respectively. Since a gold coin is worth more than a silver coin, . Hence . Since a silver coin is worth less than a gold coin, . Hence . Therefore . Hence . Because is a positive integer, it follows that is a factor of with . Therefore we need to count the factors of which are greater than . There are such factors.
A network of pathways lead from a single opening to three bins, labelled , , as shown. If a ball is dropped into the opening, it will follow a path and land in one of the bins. Every time a path splits, it is equally likely for the ball to follow either of the downward paths. Ellen drops two balls, one after the other, into the opening. What is the probability that the two balls land in different bins?
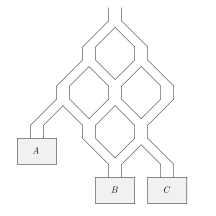
- A.
- B.
- C.
- D.
- E.
There are different locations at which the path splits, and we label these splits to , as shown.
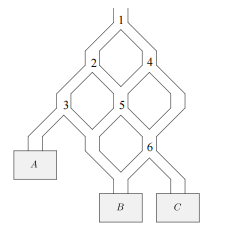
We begin by determining the probability that a ball lands in the bin labelled .
There is exactly one path that leads to bin .
This path travels downward to the left at each of the three splits labelled , and .
At each of these splits, the probability that a ball travels to the left is , and so the probability that a ball lands in bin is .
Next, we determine the probability that a ball lands in the bin labelled .
There are exactly three paths that lead to bin .
One of these paths travels downward to the right at each of the three splits labelled , and .
Thus, the probability that a ball lands in bin by following this path is .
A second path to bin travels downward to the right at split , to the left at split , to the right at split , and to the right at split .
The probability that a ball follows this path is .
The third and final path to bin travels left at split , and to the right at each of the three splits , and .
The probability that a ball follows this path is also .
The probability that a ball lands in bin is the sum of the probabilities of travelling each of these three paths or
Finally, we determine the probability that a ball lands in bin .
There are six different paths that lead to bin , and we could determine the probability that a ball follows each of these just as we did for bins and .
However, it is more efficient to recognize that a ball must land in one of the three bins, and thus the probability that it lands in bin is minus the probability that it lands in bin minus the probability that it lands in bin , or
The probability that the two balls land in different bins is equal to minus the probability that the two balls land in the same bin.
The probability that a ball lands in bin is , and so the probability that two balls land in bin is .
The probability that a ball lands in bin is , and so the probability that two balls land in bin is .
The probability that a ball lands in bin is , and so the probability that two balls land in bin is .
Therefore, the probability that the two balls land in different bins is equal to
A rectangle with dimensions by is tilted so that one corner is above a horizontal line, as shown. To the nearest centimeter, determine the height of vertex above the horizontal line.
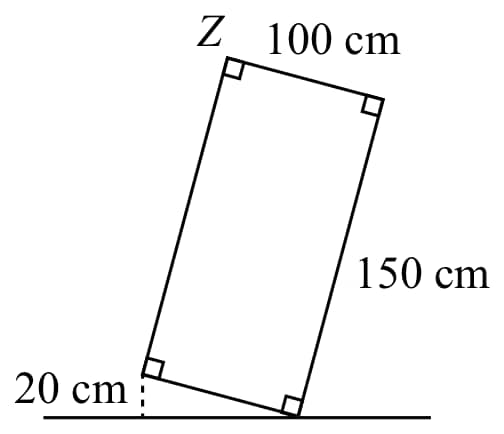
- A.
- B.
- C.
- D.
- E.
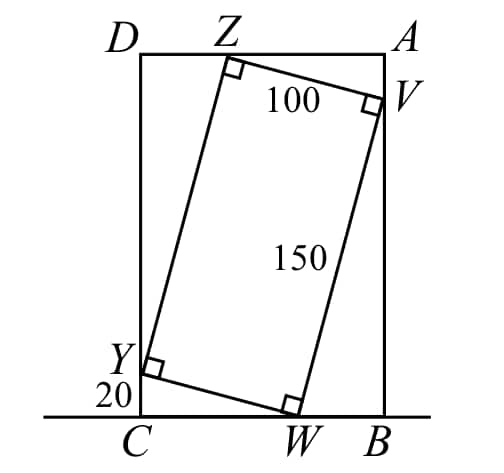
Since is a rectangle, then and . Since is right-angled at , by the Pythagorean Theorem,
Since , then . The height of above the horizontal line is equal to the length of , which equals which equals . Now is right-angled at and is right-angled at . Also, by Triple Perpendicular Model, is similar to .
Therefore, and so . Finally, . Rounded to the nearest integer, is .
A rectangular box contains a sphere of radius and eight smaller spheres of radius . The smaller spheres are each tangent to three sides of the box, and the larger sphere is tangent to each of the smaller spheres. What is ?
- A.
- B.
- C.
- D.
- E.
Let one of the corners be . We can orient the box such that the center of the small sphere closest to the corner is , and the center of the large sphere is .
Since the two spheres are tangent, the distance between their centers is , so . Solving,
Let be the point in the same plane as the centers of the top spheres equidistant from said centers. Let be the analogous point for the bottom spheres, and let be the midpoint of and the center of the large sphere. Let and be the points at which line intersects the top of the box and the bottom, respectively.
Let be the center of any of the top spheres (you choose!). We have , and , so . Similarly, . and are clearly equal to the radius of the small spheres, . Thus the total height is , or .
For how many ordered triples of integers with and and is the sum of three six-digit positive integers divisible by ?
- A.
- B.
- C.
- D.
- E.
Set . We can rearrange as follows: and so .
We need to determine for which values of , , and the integer is divisible by .
Observe that , and since and have no prime factors in common, will be divisible by exactly when it is divisible by both and .
Since is odd, it is not a multiple of , and so is a multiple of exactly when is a multiple of .
Factoring gives , and since is not a multiple of , we get that has a factor of but not a factor of .
Therefore, is a multiple of exactly when is a multiple of .
We now have that is a multiple of exactly when is a multiple of and a multiple of , or equivalently, when is a multiple of .
Since is a multiple of , is a multiple of exactly when is a multiple of .
The digits , , and are each between and inclusive, so is at least and at most . The only multiples of between and are and , so we must have that or .
To answer the question, we count the number of triples of integers, each between and inclusive, for which or .
First, suppose . If , then . In this case, we can have and , or and , or and , and so on to and . This gives a total of triples. If , then . In this case, we can have and , and , and so on to and for a total of triples. Continuing in this way, there are triples when , triples when , triples when , triples when , triples when , triples when , and there is one triple when . The number of triples when is .
Now assume . If , then , which is impossible given that and . There are no triples with . Similarly, if , then there are no triples. If , then , which means and , so there is only one triple. If , then , so either and or and . There are triples in this case. If , then , and there are triples. Continuing in this way, when A=, there are triples, when , there are triples, when , there are triples, when , there are triples, and when , there are triples. The number of triples when is . The number of triples is .
Some integers with have the property that the product of the digits of is equal to . If is the number of such integers , what is the integer formed by the rightmost two digits of ?
- A.
- B.
- C.
- D.
- E.
There are no -digit integers with the given property. This is because the product of the digits of a -digit number is at most .
Observe that . We are essentially looking for products of , , or digits that equal . The only digit that is a multiple of is itself, so no matter how many digits has, exactly two of its digits must be . The number of -digit numbers with the given property is , since if two of the digits are , the third must be . There are three -digit numbers with one digit equal to and two digits equal to . They are , , and .
If has four digits, then two digits are and the other two digits have a product of . The only ways to express as a product of two integers is and . In either case, there are six ways to choose where the two digits equal to go. They are
55_ _
5_5_
5__5
_55_
_5_5
__55
In each of these cases, there are ways to place the remaining digits. There are also two choices for the remaining two digits ( and or and ), so the number of -digit numbers with the given property is .
Using a similar method of counting, we conclude that if has digits, then there are ways to place the two digits that are equal to . The remaining three digits must have a product of , so they must be , , and or , , and or , , and . If the remaining digits are , , and , then there are choices of where to place the remaining digits. This is because once the is placed, the last two digits must be (there is no choices). If the remaining digits are , , and , then there are ways to place the remaining digits. This is because there are ways to order the digits , , and . Finally, if the remaining digits are all , then there is only one way to place the digits. Thus, there are five-digit numbers with the given property.
The total number of integers with with the property that the product of the digits is is . The integer formed by the rightmost digits of is .
The diameter of a circle of radius is extended to a point outside the circle so that . Point is chosen so that and line is perpendicular to line . Segment intersects the circle at a point between and . What is the area of ?
- A.
- B.
- C.
- D.
- E.
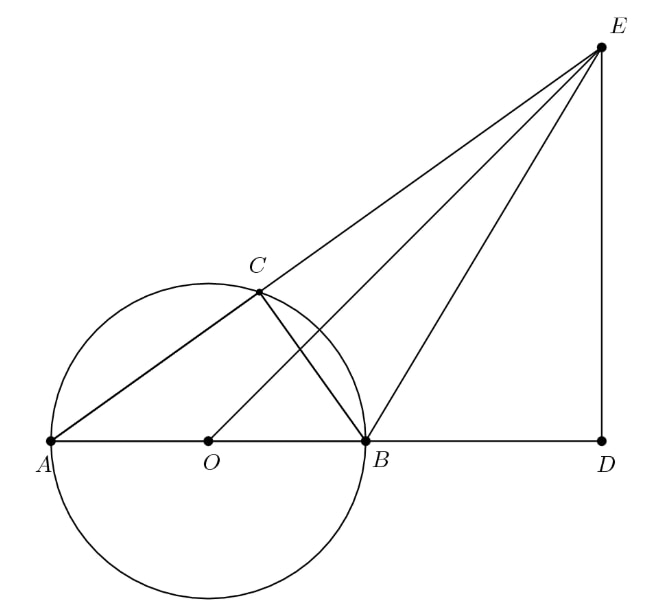
We note that by similarity. Also, since the area of and , , so the area of .
Let's call the center of the circle that segment is the diameter of . Note that is an isosceles right triangle. Solving for side , using the Pythagorean theorem, we find it to be . Calling the point where segment intersects circle , the point , segment would be . Also, noting that is a right triangle, we solve for side , using the Pythagorean Theorem, and get . Using Power of Point on point , we can solve for . We can subtract from to find and then solve for using Pythagorean theorem once more:
,
.
Now to solve for : ,
Note that is a right triangle because the hypotenuse is the diameter of the circle. Solving for area using the bases and , we get the area of triangle to be .
Suppose that and are both quadratic functions with quadratic coefficient . If and , determine .
- A.
- B.
- C.
- D.
- E.
If and , by the given conditions,
①;
②.
①② gives , so ;
②① gives , .
Also, by , we have .
∴ and ,
∴ .
The answer is
What is the number of positive integer values of such that
has no real solution for ?
- A.
- B.
- C.
- D.
- E.
Since the floor function only outputs integers and is an integer, must be an integer. Let for integers (to prevent the number under the square root from being negative). If is incremented by will always increase. While or may not increase, they will never decrease. Thus, is a strictly increasing function along the nonnegative integers. Clearly, and . It should be checked if there is an integer such that (if not, the integer where is as closest to as possible). Clearly, and . Since is strictly increasing, if exists. In this range, can only be 44 and can only be .
Then, , which lies in the range. Hence, . By the strictly increasing behavior of , the values are distinct and the only values of that can be one of the first positive integers. Thus, exactly of those integers are covered by , so the number of integers not covered by is .
Let be the set of circles in the coordinate plane that are tangent to each of the three circles with equations and . What is sum of the areas of all circles in .
- A.
- B.
- C.
- D.
- E.

There are two circles that are externally tangent to the two small circles and internally tangent to the large circle. Here and . (blue part)
There are two circles that are internally tangent to the concentric circles and externally tangent to the other circle. Here and . (red part)
There are two circles that are internally tangent to the big and non-center circles, but externally tangent to the small center circle. Here and . (green part)
There are two circles that are internally tangent to all three circles. Here and . (brown part)
The sum of area of all circles is .
How many strings of length formed from the digits , , , , are there such that for each , at least of the digits are less than ? (For example, satisfies the condition because it contains at least digit less than , at least digits less than , at least digits less than , and at least digits less than . The string does not satisfy the condition because it does not contain at least digits less than .)
- A.
- B.
- C.
- D.
- E.
Suppose . Then let's do the casework.
① If numbers are all distinct, .
② If one number is counted twice, .
③ If two numbers are counted twice, .
④ If one number is counted times, .
⑤If one number is counted times and the others are counted twice, .
⑥ If one number is counted times, .
⑦ If one number is counted times, only 1 possible way.
In total, .
Four regular hexagons surround a square with side length , each one sharing an edge with the square, as shown in the figure below. The area of the resulting -sided outer nonconvex polygon can be written as , where , , and are integers and is not divisible by the square of any prime. What is ?
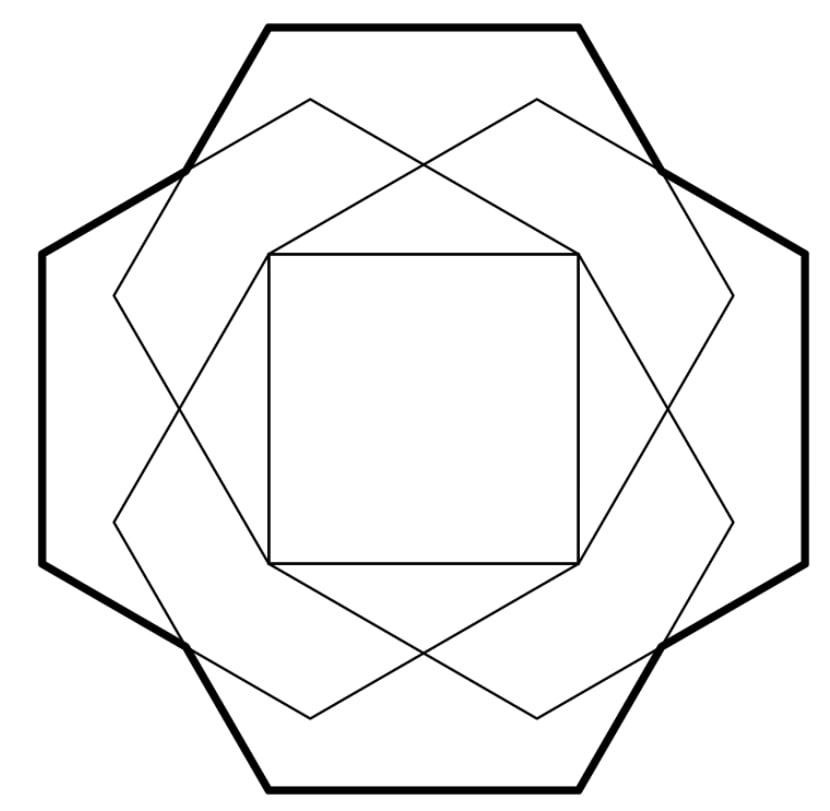
- A.
- B.
- C.
- D.
- E.
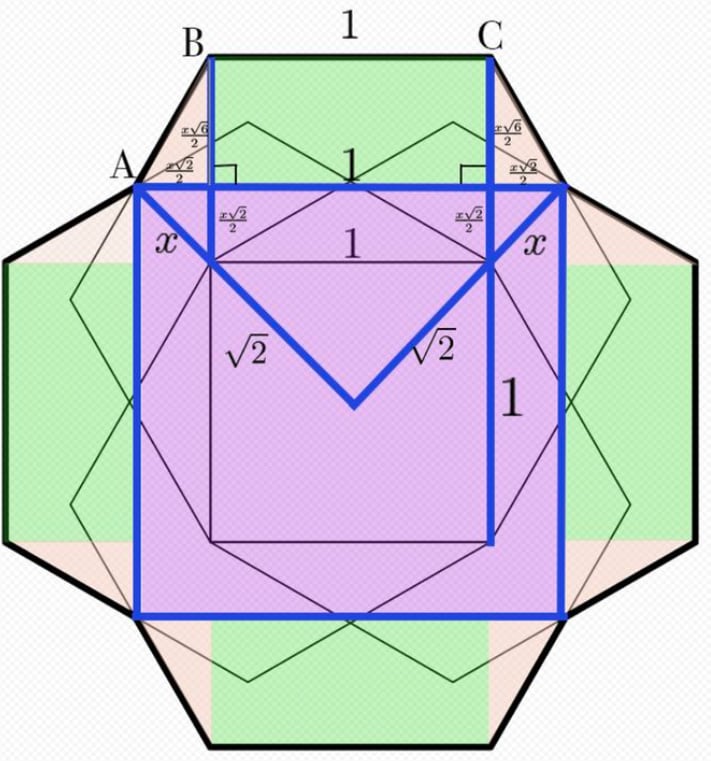
Note that each of the green sections is a rectangle, so its interior angles are all Since , every one of the orange sections is a right triangle.
Define to be the distance from the corner of the square with side length to the corner of the larger blue square. Due to the sides of the two squares being parallel to each other, the large blue triangle is a right triangle. By similarity, the smaller blue triangles are also and have side lengths of and . By triangle relations, the largest altitude of the orange triangle is
Now, we can find the height of the hexagon to obtain an equation in terms of . Consider a hexagon with side length , where point is the foot of the perpendicular dropped from , bisecting :
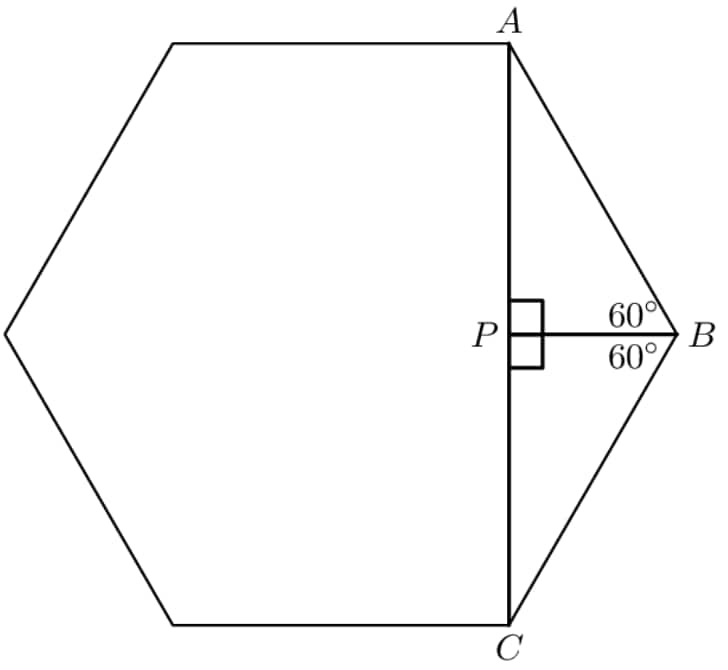
Note that triangles and are congruent -- triangles, by SAS congruence. Since the side length of this hexagon is , the length of is , by -- triangle relations. The height of the hexagon is twice this value, or
The height is also equal to the sum of the values along the long blue line, in the first diagram. Therefore, Solving and rationalizing,
The area of the dodecagon is equal to the sum of the areas of the four rectangles, eight orange triangles, and purple square. In terms of , this is
Plugging in , the area of the dodecagon is . Therefore, the answer is
Let be the number of triples of positive integers such that and . When is divided by , what is the remainder?
- A.
- B.
- C.
- D.
- E.
Suppose that and are positive integers with . We determine the number of triples with this property. (We are temporarily ignoring the size ordering condition in the original question.) Since the product has two factors of , then and have a total of two factors of . There are ways in which this can happen: both factors in , both factors in , both in , one each in and , one each in and , and one each in and . Similarly, there are ways of distributing each of the other squares of prime factors. Since includes exactly squares of prime factors and each can be distributed in ways, there are ways of building triples using the prime factors, and so there are triples with the required product.
Next, we include the condition that no pair of and should be equal. (We note that and cannot all be equal, since their product is not a perfect cube.) We count the number of triples with one pair equal, and subtract this number from . We do this by counting the number of these triples with . By symmetry, the number of triples with and with will be equal to this total. In order to have and and , for each of the squared prime factors of , either is distributed as and in each of and , or is distributed to . Thus, for each of the squared prime factors , there are ways to distribute, and so triples with and and . Similarly, there will be triples with and triples with . This means that there are triples () with the required product and with no two of equal. The original problem asked us to the find the number of triples () with the given product and with . To convert triples with no size ordering to triples with , we divide by . (Each triple corresponds to triples of distinct positive integers with no size ordering.) Therefore, the total number of triples () with the required properties is
When is divided by , the remainder is .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
