AMC 10 Daily Practice Round 2

Complete problem set with solutions and individual problem pages

Problem 1 Easy

Define a※b=\frac{a-b}{a+b} for all real numbers a and b. Find the value of 5※(4※3).

  • A.

    \frac{16}{17}

  • B.

    \frac{17}{18}

  • C.

    \frac{18}{19}

  • D.

    \frac{19}{20}

  • E.

    \frac{21}{22}

Answer:B

4※3=\frac{4-3}{4+3}=\frac{1}{7},

5※\frac{1}{7}=\frac{5-\dfrac{1}{7}}{5+\dfrac{1}{7}}=\frac{17}{18}.

∴ 5※（4※3）=\frac{17}{18}.

Link Problem
Problem 2 Easy

A bicycle has two wheels, while a tricycle has three wheels. There are a 17 such vehicles with 41 wheels. Find the number of bicycles.

  • A.

    10

  • B.

    11

  • C.

    12

  • D.

    13

  • E.

    14

Answer:A

Suppose that all vehicles are tricycles, then there are (3\times17-41)\div(3-2)=10 bicycles. Alternatively, we can also set up system of linear equations to solve the problem.

Link Problem
Problem 3 Easy

Real numbers x,y, and z satisfy the inequalities 0<x<1,-1<y<0, and 1<z<2. Which of the following numbers is necessarily positive?

  • A.

    y+x^2

  • B.

    y+xz

  • C.

    y+y^2

  • D.

    y+2y^2

  • E.

    xy+z^2

Answer:E

Notice that xy+z^2 must be positive because \left| z^2\right|\gt 1\gt \left| xy\right|. Therefore the answer is \rm E.

The other choices:

\rm (A) As x grows closer to 0, x^2 decreases and thus becomes less than y.

\rm (B) x can be as small as possible (x>0), so xz grows close to 0 as x approaches 0.

\rm (C)  For all -1<y<0, y>y^2, and thus it is always negative.

\rm (D) The same logic as above, but when -\frac 12<y<0 this time.

Link Problem
Problem 4 Easy

Two squares of side lengths 2 and 3 lie within a third square of side length 5, as shown below. What is the area of the shaded region?

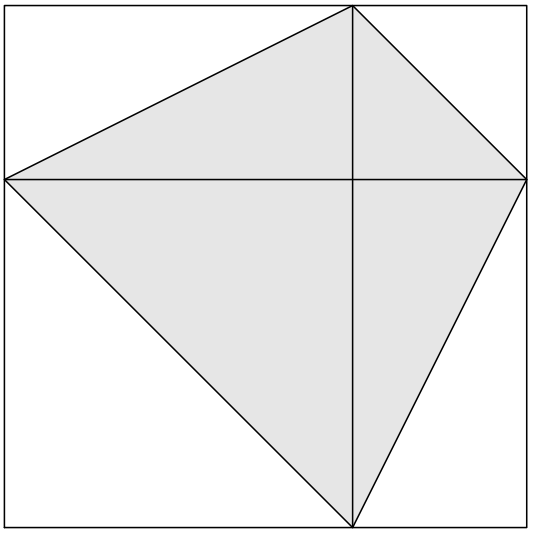
  • A.

    11

  • B.

    11.5

  • C.

    12

  • D.

    12.5

  • E.

    13

Answer:D

Each of the 4 shaded triangles can be paired with a congruent but unshaded triangle, and vice versa. Hence, the shaded region and the combined unshaded regions have the same area, so the shaded region has half the area of the entire square. The requested answer is therefore \frac{5^2}{2}=12.5.

Link Problem
Problem 5 Easy

A palindrome is a number that has the same value when read from left to right or from right to left. (For example, 12321 is a palindrome.) Determine the number of palindromes between 1000 and 2025.

  • A.

    10

  • B.

    11

  • C.

    12

  • D.

    13

  • E.

    14

Answer:B

Enumerate based on patterns: 1001, 1111, 1221, 1331, 1441, 1551, 1661, 1771, 1881, 1991, 2002.

Link Problem
Problem 6 Easy

Jason walks from his home to school. If he walks 75 meters per minute, he will be 8 minutes late; if he walks 80 meters per minute, he will be 6 minutes late. In order to arrive on time, how fast should Jason walk in meters per minute?

  • A.

    90

  • B.

    100

  • C.

    110

  • D.

    120

  • E.

    130

Answer:B

The required time is \left( 75\times 8-80\times 6 \right)\div \left( 80-75 \right)=24 minutes. 75\times \left( 24+8 \right)\div 24=100 meters per minute. Alternatively, we can also set up a rational equation to solve the problem.

Link Problem
Problem 7 Easy

Which of the following numbers is a perfect square?

  • A.

    \frac{23!24!}{3}

  • B.

    \frac{24!25!}{3}

  • C.

    \frac{25!26!}{3}

  • D.

    \frac{26!27!}{3}

  • E.

    \frac{27!28!}{3}

Answer:D

Note that for all positive n, we have \dfrac{n!\left( n+1\right)!}{3}=\dfrac{\left( n!\right)^{2}\cdot\left( n+1\right)}{3}=\left( n!\right)^{2}\cdot\dfrac{n+1}{3}.

We must find a  value of n such that \left( n!\right)^{2}\cdot\dfrac{n+1}{3} is a perfect  square. Since(n!)^2 is a perfect square, we must also have \dfrac{n+1}{3} be a perfect square. In order for \dfrac{n+1}{3} to be a perfect square, n+1 must be twice a perfect square. From the answer choices, n+1=27 works, thus, n=26 and our desired answer is (\rm D)\dfrac{26!27!}{3}.

Link Problem
Problem 8 Easy

Consider the Fibonacci Sequence 1, 1, 2, 3, 5, 8, \cdots. Starting the third number, each succeeding number is the sum of the previous two numbers. Among the first 2023 numbers in the sequence, how many of them are multiples of 5?

  • A.

    403

  • B.

    404

  • C.

    405

  • D.

    505

  • E.

    506

Answer:B

We can determine the pattern of remainders when each term in the sequence is divided by 5: 1, 1, 2, 3, 0, 3, 3, 1, 4, 0, 4, 4, 3, 2, 0, 2, 2, 4, 1, 0, 1, 1, 2, 3, \cdots. We find that a remainder of 0 appears once for every 5 numbers if the divisor is 5. As 2023\div 5=404 \ R \ 3, there are 404 such numbers.

Link Problem
Problem 9 Easy

A rectangle A B C D has A B=8 and B C=4. Points P and Q lie on sides \overline{A B} and \overline{B C}, respectively, such that A P=C Q and the area of \triangle B P Q is 6. What is P Q^2?

  • A.

    32

  • B.

    34

  • C.

    36

  • D.

    38

  • E.

    40

Answer:E

Since the area of \triangle B P Q is 6, we get that \frac{B P \cdot B Q}{2}=6. Thus, B P \cdot B Q=12. Let A P=Q C=x. Then B P=4-x and B Q=8-x, so (4-x)(8-x)=12. Expanding and factoring gives (x-2)(x-10)=0, so either x=2 or x=10.

If x=10, then B P=-6 and B Q=-2, which is impossible, so thus x=2. This gives B P=2 and B Q=6. Since A B C D is a rectangle, \angle B=90^{\circ}, so applying the Pythagorean Theorem on \triangle B P Q gives 2^2+6^2=P Q^2. Thus, P Q^2=4+36=40.

Link Problem
Problem 10 Easy

Cards labeled from 1 to 9 are distributed to students A, B, and C, three cards each person without repetition. The following are the conversations between the students.

A: The three numbers on my cards form an arithmetic sequence.

B: Me too.

C: Only my cards do not form an arithmetic sequence.

Suppose that everyone is telling the truth, find the minimum of the sum of the numbers in three cards of C.

  • A.

    6

  • B.

    7

  • C.

    8

  • D.

    9

  • E.

    10

Answer:D

As the numbers of A and B form arithmetic sequences, their sums must be multiples of 3. The sum of 9 cards is 45, which is also a multiple of 3. Therefore, the sum of C is also a multiple of 3. The sum of C can not be 6=(1+2+3), so the sum is at least 9. Check and find 9 is the correct answer.

A: (9,8,7)

B: (5,4,3)

C: (1,2,6)

Link Problem
Problem 11 Medium

Consider positive integers a,b,c,d such that ab=cd, which of the following is a possible value of a+b+c+d?

  • A.

    97

  • B.

    101

  • C.

    301

  • D.

    401

  • E.

    None of the above

Answer:C

Since 97, 101, and 401 are both prime and 301=7\times 43.

Let a=mn, b=pq, c=mp, d=nq, m, n, p, q\in {{\mathbb{N}}^{*}},

Then a+b+c+d=mn+pq+mp+nq=(m+q)(n+p)，

So we are good as long as a+b+c+d is not prime.

For example, 301=7\times 43=(1+6)\cdot (1+42).

This is true when a=1, b=252, c=42, d=6.

Link Problem
Problem 12 Medium

In the coordinate system, the x and y coordinates of the intersection point between lines y=x-k and y=kx+2 are both integers. How many possible values of k are there?

  • A.

    4

  • B.

    5

  • C.

    6

  • D.

    7

  • E.

    8

Answer:A

Construct the system \begin{cases}y=x-k ①\\ y=kx+2② \\ \end{cases}.

Plug the first equation into the second equation, we have x\left( 1-k \right)=k+2.

It is clear that 1-k\ne 0, so we have x=\frac{k+2}{1-k}=-1+\frac{3}{1-k}.

When 1-k=\pm 3 or \pm 1, x is an integer, and now y is also an integer.

Therefore, k=\{4,2,0,-2\}, four of them.

Link Problem
Problem 13 Medium

Let ABCD be a convex quadrilateral such that \angle DAB=\angle DBC=90{}^\circandDA=AB=6. Let E be the intersection of the diagonals AC and BD. If BE=2\sqrt{2}, find the area of ABCD.

  • A.

    30

  • B.

    36

  • C.

    48

  • D.

    54

  • E.

    60

Answer:D

Construct AH\bot BD.

∵ \angle DAB=90{}^\circ, DA=AB=6,

∴ BD=\sqrt{D{{A}^{2}}+A{{B}^{2}}}=6\sqrt{2}.

∵ AH\bot BD,

∴ AH=BH=DH=\frac{1}{2}BD=3\sqrt{2}, \angle AHE=90{}^\circ,

∵ BE=2\sqrt{2},

∴ EH=BH-BE=3\sqrt{2}-2\sqrt{2}=\sqrt{2},

∵ \angle AHE=\angle CBE=\angle DBC=90{}^\circ, \angle AEH=\angle CEB,

∴ \triangle AHE \sim \triangle CEB,

∴ \frac{AH}{BC}=\frac{EH}{BE}, or \frac{3\sqrt{2}}{BC}=\frac{\sqrt{2}}{2\sqrt{2}}, BC=6\sqrt{2},

∴ {{A}_{\triangle BCD}}=\frac{1}{2}BD\times BC=\frac{1}{2}\times 6\sqrt{2}\times 6\sqrt{2}=36,

{{A}_{\triangle ABD}}=\frac{1}{2}AD\times AB=\frac{1}{2}\times 6\times 6=18,

∴ {{A}_{ABCD}}={{A}_{\triangle BCD}}+{{A}_{\triangle ABD}}=36+18=54.

Therefore, A_{ABCD}=54.

Link Problem
Problem 14 Medium

Circles A, B, and C each have radius 1. Circles A and B share one point of tangency. Circle C has a point of tangency with the midpoint of \overline{AB}. One side of rectangle D is tangent to both circles A and B, and its opposite side is tangent to circle C. The other two sides are tangent to circles A and B, respectively. What is the area of the part that is inside the rectangle but not inside the circle?

  • A.

    12-3\pi

  • B.

    16-3\pi

  • C.

    10-2\pi

  • D.

    14-2\pi

  • E.

    10-3\pi

Answer:C

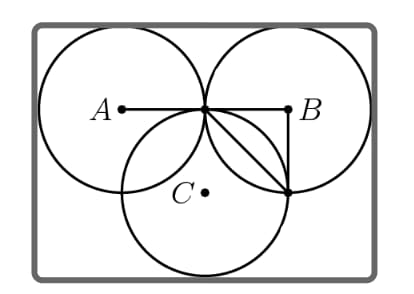
By the principle of inclusion-exclusion, it can be deduced that the desired area is equal to the area of the rectangle D minus the sum of the areas of the three circles A,B, and C, plus the overlapping area between circle C and circles A and B.

Then, we can compute the shaded area as the area of half of C plus the area of the rectangle minus the area of the two sectors created by A and B. This is \dfrac{\pi(1)^{2}}{2}+(2)(1)-2 \cdot \dfrac{\pi(1)^{2}}{4}=2.

The area of the rectangle is 4\times 3=12, so the area is 12-2\pi-2=10-2\pi.

Link Problem
Problem 15 Medium

Consider a 20-problem test with multiple choices and fill-in-the-blanks. Each multiple choice worth 4 points and each fill-in-the-blank worth 6 points. The overall correct rate is 53\% (accross the problems). In addition, the correct rate of fill-in-the-blanks is 45\% and the average score is 53.2. Determine the correct rate of multiple choices.

  • A.

    52

  • B.

    55

  • C.

    60

  • D.

    63

  • E.

    65

Answer:E

Average number of problems correct: 20\times53\%=10.6.

Average number of correct fill-in-the-blanks: (53.2-4\times10.6)\div (6-4)=5.4, so average number of correct multiple choices: 10.6-5.4=5.2.

There are 5.4\div45\%=12 multiple choices, so there are 20-12=8 fill-in-the-blanks.

Correct rate on multiple choices: \frac{5.2}{8}\times 100 \% =65\%.

Link Problem
Problem 16 Medium

In how many ways can 18 apples and 6 oranges be arranged in a line such that any 2 oranges are separated by at least 3 apples?

  • A.

    60

  • B.

    72

  • C.

    84

  • D.

    96

  • E.

    108

Answer:C

Observe that for each such arrangement, we can remove 3 apples between each of the 5 pairs of adjacent orange (i.e. pairs of orange with no orange between them) to obtain an arbitrary arrangement of 18-3 \cdot 5=3 apples and 6 oranges. Conversely, starting with any arrangement of 3 apples and 6 oranges, adding 3 apples between each pair of adjacent oranges yields an arrangement of 18 apples and 6 oranges such that any 2 oranges are separated by at least 3 apples. Hence, the number of desired arrangements equals the number of arrangements of 3 apples and 6 oranges, or \left(\begin{array}{l}9 \\ 3\end{array}\right)=(\mathbf{C}) 84.

Link Problem
Problem 17 Medium

The roots of equation {{x}^{3}}+a{{x}^{2}}+bx+c=0 with respect to x are a,b,c, respectively, while a,b,c are rational numbers that are not all 0. Determine a+b+c.

  • A.

    -8

  • B.

    -1

  • C.

    0

  • D.

    1

  • E.

    8

Answer:B

By Vieta's Formula on higher power,

\begin{cases}a=-\left( a+b+c \right) \\ b=ab+bc+ca \\ c=-abc \\ \end{cases}. As c=-abc, we have c=0 or ab=-1.

① If c=0, then \begin{cases}2a+b=0 \\ b=ab \\ \end{cases}. Solve to get \left( 0,0,0 \right) (not applicable) or \left( 1,-2,0 \right);

② If ab=-1, then \begin{cases}ab+b+c=0 \\ b=bc+ca-1 \\ \end{cases}. Solve to get \left( 1,-1,-1 \right).

Therefore, \left( a,b,c \right)=\left( 1,-2,0 \right) or \left( 1,-1,-1 \right).

(a,b,c)=(1,-2,0) or (a,b,c)=(1-1,-1). Each case gives the sum of -1.

Link Problem
Problem 18 Medium

Refer to the figure below. In parallelogram ABCD, AD=8. Construct a circle from D such that it is tangent to both AB and BC with tangent points H and G, repsectively. The circle also intersects with AD and DC at E and F, respectively. If 5AE=4DE and 8CF=DF, determine the perimeter of parallelogram ABCD.

  • A.

    32

  • B.

    34

  • C.

    36

  • D.

    38

  • E.

    40

Answer:C

Let AB=x, then CF=\frac{x}{9}. Also, AE=\frac{4}{9}\cdot 8=\frac{32}{9} and ED=\frac{5}{9}\cdot 8=\frac{40}{9}.

∵ C{{G}^{2}}=CF\cdot CD=\frac{{{x}^{2}}}{9},

∴ CG=\frac{x}{3}.

∵ A{{H}^{2}}=AE\cdot AD=\frac{32}{9}\cdot 8,

∴ AH=\frac{16}{3} and HB=x-\frac{16}{3}.

By BC=BG+GC=BH+GC, we have 8=x-\frac{16}{3}+\frac{x}{3},

∴ x=10,

∴ P_{ABCD}=\left( 8+10 \right)\cdot 2=36.

Link Problem
Problem 19 Hard

Suppose that f\left( x \right) and g\left( x \right) are both quadratic functions with quadratic coefficient 1. If g\left( 6 \right)=35 and \frac{f\left( -1 \right)}{g\left( -1 \right)}=\frac{f\left( 1 \right)}{g\left( 1 \right)}=\frac{21}{20}, determine f\left( 6 \right).

  • A.

    -35

  • B.

    0

  • C.

    1

  • D.

    35

  • E.

    \frac{147}{4}

Answer:D

If f\left( x \right)={{x}^{2}}+ax+b and g\left( x \right)={{x}^{2}}+cx+d, by the given conditions,

20\left( 1-a+b \right)=21\left( 1-c+d \right)\cdots \cdots①;

20\left( 1+a+b \right)=21\left( 1+c+d \right)\cdots \cdots②.

①+② gives 40+40b=42+42d, so 20b=1+21d;

①-② gives -40a=-42c, 20a=21c.

Also, by g\left( 6 \right)=35, we have 36+6c+d=35.

∴ 36+6\times \frac{20}{21}a+\frac{20b-1}{21}=35 and 6a+b=-1,

∴ f\left( 6 \right)=36+6a+b=35.

Let h\left( x \right)=21g\left( x \right)-20f\left( x \right).

We can readily get h\left( x \right) is also a quadratic function with quadratic coefficient 1.

Also, h\left( -1 \right)=21g\left( -1 \right)-20f\left( -1 \right)=0, h\left( 1 \right)=21g\left( 1 \right)-20f\left( 1 \right)=0,

∴ h(x)=(x+1)(x-1)={{x}^{2}}-1,

∴ h\left( 6 \right)=21g\left( 6 \right)-20f\left( 6 \right)={{6}^{2}}-1=35,

∴ 21\times 35-20f\left( 6 \right)=35 and f\left( 6 \right)=35.

Link Problem
Problem 20 Medium

Three diagonals are drawn in a regular hexagon of side length 1, splitting the hexagon into several regions. What is the least possible area of such a region?

  • A.

    \frac{\sqrt{3}}{24}

  • B.

    \frac{\sqrt{3}}{18}

  • C.

    \frac{\sqrt{3}}{16}

  • D.

    \frac{\sqrt{3}}{12}

  • E.

    \frac{\sqrt{3}}{8}

Answer:A

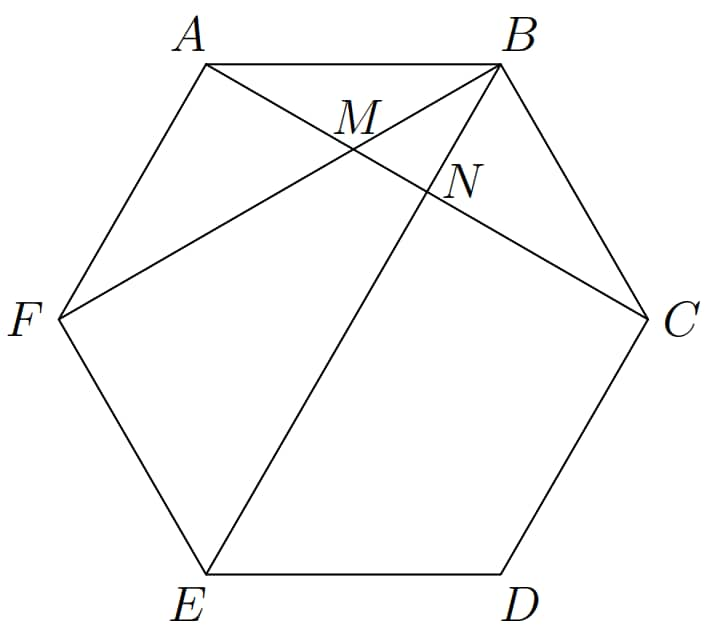
Above, the two diagonals stemming from a common vertex are \overline{B E} and \overline{B F}, which form the smallest angle possible of \angle E B F=30^{\circ}, and the third diagonal \overline{A C} bounds \angle E B F as tightly as possible.

The area we seek is A_{\triangle B M N}. First, triangles A B M and C F M are similar in ratio \frac{A B}{C F}=\frac{1}{2}, so \frac{A M}{C M}=\frac{1}{2} or, equivalently, \frac{A M}{A C}=\frac{1}{3}. Additionally, A N=C N by symmetry, which yields that \frac{C N}{A C}=\frac{1}{2}. Therefore, \frac{M N}{A C}=1-\frac{A M}{A C}-\frac{C N}{A C}=1-\frac{1}{3}-\frac{1}{2}=\frac{1}{6} . Now, triangles B M N and B A C share an altitude from B, implying \frac{A_{\triangle B M N}}{A_{\triangle B AC}}= \frac{M N}{A C}=\frac{1}{6}. Then, since \triangle A B C is a 30-30-120 triangle with leg length A B=1, it has area \frac{\sqrt{3}}{4}, giving us the requested answer of A_{\triangle B M N}=(\mathbf{A}) \frac{\sqrt{3}}{24}.

Link Problem
Problem 21 Hard

Jacob uses the following procedure to write down a sequence of numbers. First he chooses the first term to be 6. To generate each succeeding term, he flips a fair coin. If it comes up heads, he doubles the previous term and subtracts 1. If it comes up tails, he takes half of the previous term and subtracts

1. The probability that the n-th term is an integer is less than \frac{1}{2}. What is the minimum value of n?

  • A.

    3

  • B.

    4

  • C.

    5

  • D.

    6

  • E.

    7

Answer:D

We construct a tree showing all possible outcomes that Jacob may get after 3 flips; we can do this because there are only 8 possibilities:6\left\{ \begin{array}{l} {H:11\left\{ \begin{array}{l} {H:21\left\{ \begin{array}{l} {H:\boxed {41}}\\{T:9.5} \end{array}\right. }\\{T:4.5\left\{ \begin{array}{l} {H:\boxed {8}}\\{T:1.25} \end{array}\right. } \end{array}\right. }\\{T:2\left\{ \begin{array}{l} {H:3\left\{ \begin{array}{l} {H:\boxed {5}}\\{T:0.5} \end{array}\right. }\\{T:0\left\{ \begin{array}{l} {H:\boxed {-1}}\\{T:\boxed {-1}} \end{array}\right. } \end{array}\right. } \end{array}\right.

Similarily, we found the probabililty for the 5-th term to be an integer is \frac{1}{2}, for the 6-th term to be an integer is \frac{15}{32}. So the answer is 6.

Link Problem
Problem 22 Hard

Consider four spheres in the same space with radii 2, 2, 3, 3, respectively. Each of the four spheres are externally tangent to the other three spheres. There is a fifth sphere such that is externally tangent to all four original spheres. Determine the radius of the fifth sphere.

  • A.

    \frac 14

  • B.

    \frac 13

  • C.

    \frac 12

  • D.

    \frac{6}{11}

  • E.

    \frac{7}{12}

Answer:D

Let the centers of the spheres with radii 3 be A and B, respectively. Similarly, let the centers of the spheres with radii 2 be C and D, respectively.

Then we can readily get AB=6 and CD=4.

In addition, AC=AD=BC=BD=5.

Let the center of the fifth sphere be O and radius r. So O is inside the tetrahedron ABCD. AO=BO=3+r and CO=D0=2+r. Take the midpoint of AB and denote as E. Connect CE and DE, so CE\bot AB and DE\bot AB.

∴ Plane CDE is the perpendicular bisector plane of AB and we denote as a,

∴ O is in the plane CDE. Also, by OC=OD=2+r, we have O is in the perpendicular bisector plane of CDE,

∴ O is on the altitude of the base CD of \triangle CED, which is EF. F is the midpoint of CD. Then, we calculate that ED=EC=\sqrt{{{5}^{2}}-{{3}^{2}}}=4,

∴ \triangle ECD is an equilateral triangle adn EF=\frac{\sqrt{3}}{2}ED=2\sqrt{3}, OF=\sqrt{O{{C}^{2}}-C{{F}^{2}}}=\sqrt{{{(2+r)}^{2}}-{{2}^{2}}}=\sqrt{r(4+r)}, OE=\sqrt{O{{A}^{2}}-A{{E}^{2}}}=\sqrt{{{(3+r)}^{2}}-{{3}^{2}}}=\sqrt{r\left( 6+r \right)},

Plug in, OE+OF=EF=2\sqrt{3}.

The final equation is \sqrt{r(4+r)}+\sqrt{r(6+r)}=2\sqrt{3}. Solve to get r=\frac{6}{11}.

​

Link Problem
Problem 23 Hard

Let \lfloor x \rfloor denote the greatest integer less than or equal to x. Find the number of positive integer n that satisfy 2023\left\lfloor n\sqrt{{{2022}^{2}}+1} \right\rfloor=n\left\lfloor 2023\sqrt{{{2022}^{2}}+1} \right\rfloor.

  • A.

    0

  • B.

    1011

  • C.

    2022

  • D.

    3033

  • E.

    4044

Answer:E

By 2023\sqrt{{{2022}^{2}}+1}-2023\times 2022=2023\times \frac{1}{\sqrt{{{2022}^{2}}+1}+2022}<{}1,

∴ 2023\times 2022<{}2023\sqrt{{{2022}^{2}}+1}<{}2023\times 2022+1,

∴ \left\lfloor 2023\sqrt{{{2022}^{2}}+1} \right\rfloor=2023\times 2022,

∴ n\times 2023\times 2022=2023\left\lfloor n\sqrt{{{2022}^{2}}+1} \right\rfloor,

∴ \left\lfloor n\sqrt{{{2022}^{2}}+1} \right\rfloor=2022n,

So to get 2022n\leqslant n\sqrt{{{2022}^{2}}+1}<{}2022n+1, or n<{}\sqrt{{{2022}^{2}}+1}+2022, n\leqslant 4044.

Link Problem
Problem 24 Hard

Travis has to babysit the terrible Thompson triplets. Knowing that they love big numbers, Travis devises a counting game for them. First Tadd will say the number 1, then Todd must say the next two numbers (2 and 3), then Tucker must say the next three numbers (4, 5, 6), then Tadd must say the next four numbers (7, 8, 9, 10), and the process continues to rotate through the three children in order,each saying one more number than the previous child did, until the number 10000 is reached. What is the 2023^{\text{rd}} number said by Tadd?

  • A.

    5743

  • B.

    5885

  • C.

    5983

  • D.

    6001

  • E.

    6011

Answer:C

Define a round as one complete rotation through each of the three children.

We create a table to keep track of what numbers each child says for each round.

    Round            Tadd            Todd            Tucker
       1                   1              2\sim3           4\sim6
       2              7\sim10      11\sim15      16\sim21
       3            22\sim28      29\sim36      37\sim45
       4            46\sim55      56\sim66      67\sim78

Notice that at the end of the n , the last number said is the 3n^{\text{th}} triangular number.

Tadd says 1 number in round 1, 4, numbers in round 2, 7 numbers in round 3, and in general 3n-2 numbers in round n, At the end of round n, the number of numbers Tadd has said so far is 1+4+7+\cdots+(3n-2)=\frac{n(3n-1)}{2}, by the arithmetic series sum formula. We therefore want the smallest positive integer k such that 2023 \leqslant\frac{k(3k-1)}{2}. The value of k will tell us in which round Tadd says his 2023^{\text{th}} number. Through guess and check (or by actually solving the quadratic inequality), k=37.

Now, using our formula \frac{n(3n-1)}{2}, Tadd says 1926 numbers in the first 36 rounds, so we are looking for the (2023-1926)=97^{\text{th}} number Tadd says in the 37^{\text{th}} round.

We found that the last number said at the very end of the n^{\text{th}} round is the 3n^{\text{th}} triangular number.

For n=36, the 108^{\text{th}} triangular number is \frac{108\times(108+1)}{2}=5886. Thus the answer is 5886+97=\boxed{(\text{C})5983}.

Link Problem
Problem 25 Hard

For every integer n, we can represent it by n=2^ka_n, k is a nonnegative integer and a_n is an odd number. S_n=a_1+a_2+a_3+\cdots+a_n. Find S_{128}.

  • A.

    1366

  • B.

    2390

  • C.

    4098

  • D.

    5462

  • E.

    6878

Answer:D

By the definition, we know a_n=\frac{n}{2^k}=n-\frac{n}{2}-\frac{n}{4}-\cdots-\frac{n}{2^k}.

So for those n=2^k, S_{n}=1+2+3+\cdots+n-\frac{2+4+6+\cdots+n}{2}-\frac{4+8+12+\cdots+n}{4}-\cdots-\frac{n}{2^k}=\frac{(1+n)(\frac{n-1}{1}+1)}{2}-\frac{(2+n)(\frac{n-2}{2}+1)}{2\times 2}-\frac{(4+n)(\frac{n-4}{4}+1)}{2\times 4}\cdots-\frac{(n+n)}{2\times 2^k}=\frac{n(n+1)}{2}-\Sigma_{i=1}^k \frac{(2^i+n)n}{2^{2i+1}}.

Let T_n=\Sigma_{i=1}^k \frac{n}{2^{i+1}}=n\Sigma_{i=1}^k \frac{1}{2^{i+1}}=n(\frac{1}{2}-\frac{1}{2^{k+1}})=n(\frac{1}{2}-\frac{1}{2n})=\frac{n}{2}-\frac{1}{2},

U_n=\Sigma_{i=1}^k \frac{n^2}{2^{2i+1}}=n^2\Sigma_{i=1}^k \frac{1}{2^{2i+1}}=n^2\cdot \frac{1}{6}(1-\frac{1}{4^k})=n^2\cdot \frac{1}{6}(1-\frac{1}{n^2})=\frac{n^2}{6}-\frac{1}{6}.

\therefore S_n=\frac{n(n+1)}{2}-T_n-U_n=\frac{n^2}{3}+\frac{2}{3}, when n=2^k, k is a nonnegative integer.

Subsitute n=128 we have S_{128}=5462.

A less rigorous but time-saving approach to the exam can be to write the first 16 terms of a_n and S_n, then you may find out S_{2^k}=S_{2^{k-1}}+4^{k-1} and S_{2^0}=1, that will also give you the answer is 1+4^0+4^1+4^2+\cdots+4^6=5462.

In computer science, there is a cool method to calculate the value of k for each n, which is k = n \& (-n), commonly referred to as "lowbit". This involves many interesting properties of binary numbers, and children interested in this topic can search and learn more about it.

Link Problem
Related Paper
AMC 10 Daily Practice Round 4 AMC 10 Daily Practice Round 3 AMC 10 Daily Practice Round 1 AMC 10 Weekly Practice Round 3
Table of Contents
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
Think Academy Powered by ChatGPT