AMC 10 Weekly Practice Round 3
Complete problem set with solutions and individual problem pages
From boys and girls, select people to form a team for the competition. If at least girl must be included, then the total number of different ways to form the team is ( ).
- A.
- B.
- C.
- D.
- E.
From the problem, the different selections can be divided into two cases:
Case 1: Exactly girl is selected. The number of different ways is
Case 2: Exactly girls are selected. The number of different ways is
According to the Addition Principle of Counting, the total number of different selections with at least girl is
Therefore, the answer is
Given different colors of paint to color the six regions and in the figure, with the condition that adjacent regions cannot be painted the same color, how many different colorings are there?

- A.
- B.
- C.
- D.
- E.
Assuming the coloring order is ,
If and are colored the same, then there are
ways.
If and are different, and and are the same, then there are
ways.
If and are different, and and are also different, then there are
ways.
Therefore, by the Addition Principle of Counting, the total number of colorings is
Hence the answer is .
Five students and participate in a certain technical competition and receive the first through fifth places. and ask about the results. The organizer tells : “Unfortunately, neither you nor won the championship.” To , the organizer says: “Of course, you are not in the last place.” Based on the organizer’s responses, how many different possible rankings of the five students are there?
- A.
- B.
- C.
- D.
- E.
According to the problem, and did not win the championship, and is not in the last place. We discuss two cases:
1. If is in the last place, then can be in second, third, or fourth place. Thus, there are possible positions for , and the remaining three students have possible arrangements. In this case, there are
possible rankings.
2. If is not in the last place, then and must be placed in the second, third, and fourth positions. There are possible arrangements for and , and the remaining three students also have possible arrangements. In this case, there are
possible rankings.
Therefore, in total there are
different possible rankings.
Hence, the answer is .
From and , select any three different digits to form a three-digit number. Among all such numbers, how many odd numbers that greater than can be formed?
- A.
- B.
- C.
- D.
- E.
Two cases:
If the hundreds digit is or , then there are
odd three-digit numbers.
If the hundreds digit is or , then there are
odd three-digit numbers.
Therefore, the total number of odd three-digit numbers satisfying the condition is
There are players in a chess qualifying tournament. Each pair of players plays exactly one game. In each game, the winner gets point and the loser gets points; if the game is a draw, each player gets points. After all the games are finished, players with at least points can advance. What is the maximum possible number of players who can advance in this tournament?
- A.
- B.
- C.
- D.
- E.
Sixteen players play a total of games, and the total number of points is . Since a player must score at least points to qualify, the number of qualifiers cannot exceed
First, we prove that having qualifiers is impossible. Suppose there are qualifiers; then there would be non-qualifiers. The non-qualifiers play games among themselves, earning a total of points. Thus, the qualifiers can earn at most points in total. Since the sum of the players’ points is , at least one of them must have fewer than points, contradicting the assumption that all are qualifiers. Hence, there can be at most qualifiers.
Next, we show that having qualifiers is possible. Among the players, there are games, totaling points. If all these games end in draws, each player gets points. In addition, each of these players must play against the other non-qualifiers; if each of these games is won, then each player earns another points. Therefore, each of the players has points, meeting the qualifying standard.
Thus, the answer is .
The number of six-digit numbers formed from the digits in which odd and even digits alternate and no digit is repeated is ( ).
- A.
- B.
- C.
- D.
- E.
The total number of alternating arrangements of odd and even digits using these six digits is
Among them, the arrangements with in the first place are
Therefore, the number of six-digit numbers satisfying the condition is
Thus, the correct answer is .
Five people and two others stand in a row, with not at either end, and exactly two people standing between and . How many different arrangements are there?
- A.
- B.
- C.
- D.
- E.
Since there are exactly people between and , the block consisting of and the two people between them must occupy either the first four positions or the last four positions.
1. When the block occupies the first four positions, the last position remains free. In this case, must be placed between and .
Arranging and : ways.
Placing between them: way.
Arranging the other two people in the remaining two positions: ways.
Thus, the number of arrangements is
2. When the block occupies the last four positions, the first position remains free. Similarly, must be placed between and .
Arranging and : ways.
Placing between them: way.
Arranging the other two people in the remaining two positions: ways.
Thus, the number of arrangements is
By the Addition Principle of Counting, the total number of arrangements is
Therefore, the answer is .
If the sum of the digits of a five-digit number is , then the total number of such five-digit numbers is ( ).
- A.
- B.
- C.
- D.
- E.
If the sum of the digits of a five-digit number is , then such numbers can be divided into three cases:
Case . The digits consist of four ’s and one .
Since the first digit cannot be , the must be in the first place and all other digits are , giving the number .
Thus, there is only possibility.
Case . The digits consist of three ’s, one , and one .
Since the first digit cannot be , the first digit must be either or . Choose one of them for the first place, and the other digit can occupy any of the remaining four positions. The rest are .
Thus, there are possibilities.
Case 3. The digits consist of two ’s and three ’s.
Since the first digit cannot be , the first digit must be . Among the remaining four places, choose two for ’s, and the rest are .
Thus, there are possibilities.
By the Addition Principle of Counting, the total number of such five-digit numbers is
Therefore, the answer is .
There are cars to be parked in adjacent parking spaces. Truck A is wider and occupies two spaces when parked, and car B cannot be parked next to truck A. How many different parking arrangements are there?
- A.
- B.
- C.
- D.
- E.
First, park truck .
If truck is not at the edge, there are possible positions. In this case, car B has possible positions. The other three cars (excluding A and B) can be arranged in ways.
If truck A is at the edge, there are possible positions. In this case, car B has possible positions. The other three cars can also be arranged in ways.
Therefore, the total number of parking arrangements is
Thus, the answer is .
Sammy uses a permutation of the six digits as his six-digit bank card password. If there is exactly one digit between the two ’s, and and are adjacent, then the number of possible passwords is ( ).
- A.
- B.
- C.
- D.
- E.
The digits and must be adjacent, which gives arrangements.
The two ’s must have exactly one digit between them, which gives arrangements.
After grouping these conditions together, the combined blocks can be permuted in ways.
Therefore, the total number of possible passwords is
Thus, the answer is .
How many non-negative integer solutions does the equation have?
- A.
- B.
- C.
- D.
- E.
This problem is equivalent to placing identical balls into distinct boxes, allowing some boxes to be empty.
Arrange the balls in a row and use dividers to separate them into groups. Since empty boxes are allowed, dividers may be adjacent. Assign the first, second, third, and fourth groups to the variables respectively.
Because the balls are identical and the dividers are also identical, this is equivalent to arranging balls and dividers in a line. The number of such arrangements is
Therefore, the answer is .
If three vertices are chosen at random from a regular decagon, the probability that the chosen three points form a right triangle is ( ).
- A.
- B.
- C.
- D.
- E.

From the vertices of a regular decagon, choosing any points gives possible selections.
Consider the regular decagon as inscribed in a circle. For the chosen points to form a right triangle, the side opposite the right angle must be a diameter.
There are ways to choose a diameter of the circle, and for each diameter, there are choices for the right-angle vertex.
Thus, the probability that the chosen points form a right triangle is
Therefore, the answer is .
Four volunteers and are assigned to three soccer fields for volunteer service. Each volunteer must be assigned, and each soccer field must have at least one volunteer. However, and cannot be assigned to the same soccer field. How many different assignment plans are there?
- A.
- B.
- C.
- D.
- E.
Since and cannot be assigned to the same soccer field, there are two possible cases:
When and each serve on different soccer fields, there are assignment plans.
When either or is assigned together with one of or to the same soccer field, there are assignment plans.
Therefore, the total number of different assignment plans is
Thus, the answer is .
A science and technology expo is held in a certain place with exhibition halls. There are volunteer slots to be assigned to these halls, with the requirements that each hall receives at least one slot and the numbers of slots assigned to the halls are all different. How many different assignment methods are there?
- A.
- B.
- C.
- D.
- E.
“The distribution method in which each hall receives at least one slot” is equivalent to choosing two gaps from the gaps between the slots to insert dividers, which gives
methods.
The distributions in which at least two halls receive the same number of slots are
for a total of
cases.
Therefore, the number of distributions in which each hall receives at least one slot and all halls receive different numbers of slots is
Thus, the answer is .
Assign doctors to units and for nucleic acid testing, with doctors assigned to each unit. Doctor cannot go to unit , and doctor can only go to unit . How many different assignment methods are there?
- A.
- B.
- C.
- D.
- E.
According to the problem, we discuss two cases:
① If goes to unit , then and are together in unit . The remaining people are divided into groups and assigned to units and . The number of arrangements is
② If does not go to unit , then must go to unit . From the remaining people, choose to be assigned to unit , and then assign the remaining people to units and . The number of arrangements is
Therefore, the total number of arrangements is
Thus, the answer is .
If one number is chosen at random from all the positive divisors of , what is the probability that this number is a perfect square?
- A.
- B.
- C.
- D.
- E.
Since ,
the positive divisors of are
a total of numbers.
Among them, the perfect squares are
a total of numbers.
Therefore, if one number is chosen at random from all the positive divisors of , the probability that it is a perfect square is
Hence, the answer is .
Assign volunteers to classrooms numbered for cleaning, with exactly one volunteer in each classroom. What is the probability that is not assigned to classroom ?
- A.
- B.
- C.
- D.
- E.
Volunteers are assigned to classrooms numbered ,
with exactly one volunteer in each classroom. The possible assignments are:
a total of .
Among these, the cases where is not assigned to classroom are:
a total of .
Therefore, the probability that is not assigned to classroom is
Thus, the answer is .
From five line segments of lengths , three are chosen at random. The probability that these three line segments can form a triangle is ( ).
- A.
- B.
- C.
- D.
- E.
Choosing any line segments, the possible sets are a total of basic events.
Among these, the sets of three line segments that can form a triangle are
a total of .
Therefore, the probability that three chosen line segments can form a triangle is
Thus, the answer is .
If three vertices are chosen at random from the eight vertices of a cube and connected to form a triangle, what is the probability that the triangle is equilateral?
- A.
- B.
- C.
- D.
- E.
The number of ways to choose any three vertices from the eight vertices to form a triangle is .
Among them, there are outcomes that form an equilateral triangle:
Therefore, the probability is , hence the answer is .
To assess students’ physical fitness, items are chosen at random from a total of events: track and field events, ball games, and martial arts events. What is the probability that the chosen items come from exactly two categories?
- A.
- B.
- C.
- D.
- E.
The total number of ways to choose items from these events is
The number of ways where all items come from the same category is
The number of ways where the items cover all three categories is
Therefore, the number of favorable cases (exactly two categories) is
So the required probability is
Hence, the answer is .
A point is chosen at random inside a circle with radius . What is the probability that the chord with midpoint has length less than ?
- A.
- B.
- C.
- D.
- E.
From the problem we have:
The chord with midpoint has length less than if and only if the distance from the circle’s center to satisfies
That is, when , the chord with midpoint has length less than .
By the geometric probability formula, the required probability is
Therefore, the answer is .
On side of triangle with area , a point is chosen at random. What is the probability that the area of is greater than ?
- A.
- B.
- C.
- D.
- E.
Let the event be
The sample space is the length of segment (see figure).
Since
we have
which simplifies to
Since by the similarity we obtain
Thus, the geometric measure of event corresponds to the length on segment .
Since we get
Therefore, the answer is .
As shown in the figure, circles , , and are mutually externally tangent and also tangent internally to the equilateral triangle . If a point is chosen at random inside equilateral triangle , what is the probability that this point lies inside triangle (the shaded region)?
- A.
- B.
- C.
- D.
- E.
As shown in the figure, let the radius of one inscribed circle be . Then
so and
Since equilateral triangle is similar to equilateral triangle ,
the probability that a randomly chosen point inside lies in triangle (the shaded region) is
Therefore, the answer is .
Since Wong is busy at work and has no time to cook lunch, he orders takeout. Suppose both Wong and the delivery person both arrive randomly between and at the entrance of Wong’s building. Suppose Wong arrived earlier than the delivery person, what is the probability that Wong waits no more than minutes for the delivery person?
- A.
- B.
- C.
- D.
- E.
Let the arrival times (in minutes after ) of the delivery person and Wong be and respectively. The event that “Wong waits no more than minutes” is event .
The sample space is and
(see figure)
.
Choose .
As shown in the figure, a sphere is inscribed in a cube of side length (the sphere is tangent to each face of the cube). If a point is chosen at random inside the cube, what is the probability that the point lies outside the sphere?
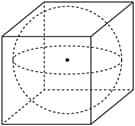
- A.
- B.
- C.
- D.
- E.
.
The radius of the inscribed sphere is , so its volume is
The volume of the cube is
Therefore, the probability that a randomly chosen point in the cube lies outside the sphere is
Thus, the answer is .
A student’s shooting accuracy for one shot is , and the probability of making two consecutive shots is . If the student has just made a shot, then what is the probability that the next shot is also successful?
- A.
- B.
- C.
- D.
- E.
If denotes the event that the -th shot is successful, then
,
Therefore,
Thus, the answer is D.
and each shoot once at the same target. The probability that hits the target is , and the probability that hits the target is . Given that the target is hit at least once, what is the probability that hits the target?
- A.
- B.
- C.
- D.
- E.
Let event be: the target is hit at least once, and event be: hits the target.
We calculate:
So,
Therefore, the answer is .
A medical device has two consumable components, and . After each use, the probability that component needs to be replaced is , and the probability that component needs to be replaced is . Given that at least one component must be replaced after the first use, what is the probability that both and need to be replaced?
- A.
- B.
- C.
- D.
- E.
Let event be: at least one component needs to be replaced after the first use, and event be: both components and need to be replaced.
Then,
By the conditional probability formula,
Therefore, the answer is .
Two players and compete for the championship in a Go match. The match follows a “best of three” format. The probability that wins any individual game is , and the outcomes of different games are independent. Given that wins the championship, what is the probability that the match lasts for games?
- A.
- B.
- C.
- D.
- E.
From the problem, the probability that wins the championship is
The probability that the match lasts for games is
Therefore, given that wins the championship, the probability that the match lasted for games is
Hence, the answer is .
Andy can choose to join from science clubs, art clubs, and sports clubs. If Andy signs up for two clubs, then given that exactly one of them is an art club, what is the probability that the other one is a sports club?
- A.
- B.
- C.
- D.
- E.
Let event be “one is an art club,” and event be “one is a sports club,”
then
Thus, .
Therefore, the answer is .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
