AMC 10 Weekly Practice Round 2
Complete problem set with solutions and individual problem pages
A store is selling a commodity. Due to reduction of purchase price by , the profit rate increased by . Then the original profit ratio of this commodity is .
- A.
- B.
- C.
- D.
- E.
Let the original cost price be dollars, and the original profit rate be .
According to the problem:
Solving this equation gives:
Answer: .
A fruit company purchased kilograms of apples at a cost of dollars per kilogram, with an additional dollars in transportation and other expenses. The estimated loss due to spoilage is . If the company hopes to make a profit after selling all the apples, what should the retail price per kilogram be?
- A.
dollars
- B.
dollars
- C.
dollars
- D.
dollars
- E.
dollars
Total cost of the purchase: dollars
Total quantity available for sale:
Let the retail price per kilogram be dollars.
Then:
Answer: The retail price per kilogram should be dollars.
A container holds of saline solution with a salt concentration of , and container holds of saline solution with a salt concentration of . If the same amount of solution is taken from both containers and poured into the other container, then stirred evenly, the resulting salt concentrations in both containers become equal. How many milliliters of solution were poured out from each container?
- A.
- B.
- C.
- D.
- E.
After exchanging, the salt concentration becomes:
Volume of exchanged solution:
Each of containers A and B had of solution exchanged.
A store purchased a batch of goods and planned to sell them at a markup. After selling of the goods at the marked-up price, the store decided to sell the remaining goods at off in order to clear the stock quickly. After all the goods were sold, the store was unexpectedly charged an additional dollars tax, which caused the actual profit to be only half of the originally expected profit. What was the cost price of this batch of goods?
- A.
dollars
- B.
dollars
- C.
dollars
- D.
dollars
- E.
dollars
Let the cost price be dollars. Then the equation is:
Solving this gives:
Answer: The cost price of the goods was dollars.
Three types of saline solutions with salt concentrations of , , and are mixed in certain proportions to obtain of a solution with a salt concentration of . If the amount of saline solution is more than that of the saline solution, how many grams of the saline solution were used?
- A.
grams
- B.
grams
- C.
grams
- D.
grams
- E.
grams
Let the mass of solution be , then the mass of solution is , and the mass of solution is .
The total salt content equation is:
Solving gives:
Then:
Answer: The masses of the saline solutions with concentrations of , , and are , , and , respectively.
The total number of students in School and School is in the ratio of .
The number of boys in School A and School B is in the ratio of .
If School A has girls and School B has girls, how many students are there in total across both schools?
- A.
- B.
- C.
- D.
- E.
Let the number of boys in School A be , then the number of boys in School B is .
According to the given ratio, we can set up the proportion:
Using the property of proportions (cross multiplication), we get:
Solving the equation gives:
Therefore, School A has boys,
and School B has boys.
The total number of students in both schools is: .
In a garage, there are some two-wheeled motorcycles and four-wheeled cars. The ratio of the number of vehicles to the number of wheels is .
What is the ratio of the number of motorcycles to the number of cars?
- A.
- B.
- C.
- D.
- E.
Let there be motorcycles and cars.
According to the problem:
Multiply both sides by :
Solving gives:
Therefore, the ratio of motorcycles to cars is
At a school, the number of students in Grade and Grade is the same, and the number of students in Grade is of that in Grade .
It is known that the number of boys in Grade is equal to the number of girls in Grade , and that the number of boys in Grade accounts for of the total number of boys across all three grades.
What fraction of the total number of students across the three grades are girls?
- A.
- B.
- C.
- D.
- E.
Let the number of boys in Grade 7 be and the number of girls be .
Then, in Grade 8, there are boys and girls.
The total number of students in Grade 9 is .
So, the total number of students across all three grades is:
Let the number of boys in Grade 9 be .
According to the problem:
Solving this gives:
So, the number of girls in Grade is:
Thus, the total number of girls across all grades is:
The fraction of girls among all students is:
Answer: .
The ratio of the number of students participating in a math competition from School A and School B is , and the ratio of the number of students who won awards is . Each school has students who did not win an award. How many students participated in the competition in total?
- A.
- B.
- C.
- D.
- E.
Let the number of students participating from School A and School B be and respectively.
According to the problem, the number of students who did **not** win awards in each school is:
Solving the equation gives:
Therefore, the total number of participants from both schools is: students.
There are two bags of fruit. Take of the fruit out of Bag and grams of fruit out of Bag , and the two bags of fruit will weigh the same. Now, if of the remaining fruit in Bag is taken out, the weight of the fruit that is still in Bag will be of the original weight of all the fruit in Bag . In the first place, there are ( ) grams of fruit in the two bags.
- A.
- B.
- C.
- D.
- E.
Let the original amount of fruit in Bag A and Bag B be grams and grams, respectively.
From Bag A, was taken out, so the remaining amount is
From Bag B, grams were taken out, so the remaining amount is
Thus,
Next, half of the remaining fruit in Bag B was taken out, so the remaining amount is
It is also given that this remaining amount equals :
Solving this equation:
Substitute back:
So the total original weight of the fruit is:
Answer: The original total weight of the fruit was grams.
There are two groups of numbers. The average of the first group is , and the average of the second group is . The overall average of the two groups combined is . What is the ratio of the number of elements in the second group to that in the first group?
- A.
- B.
- C.
- D.
- E.
There are numbers in the first group and numbers in the second group.
According to the problem,
Simplifying gives:
which leads to:
Therefore, the number of elements in the second group is of the number in the first group.
A data set containing numbers, some of which are , has mean . When all the s are removed, the data set has mean . How many s were in the original data set?
- A.
- B.
- C.
- D.
- E.
Let the number of s in the original data set be . Numbers in the original data set have sum , and the data set with the s removed has sum . Thus
Solving this equation for yields . For example, the data set could consist of copies of and copies of .
Jane plans to enter the numbers into the computer to calculate their average. When she thought she had finished entering the numbers, the computer showed that only numbers had been entered, and the average was . Assuming the numbers were entered correctly, what is the missing number?
- A.
- B.
- C.
- D.
- E.
First, estimate the value of :
If the missing number is (the largest possible value), then the average would be
;
If the missing number is (the smallest possible value), then the average would be
.
This shows that the actual average, , must lie between and .
That means can only be or .
Moreover, since the fraction must be derived from a total divided by ,
and the denominator must be divisible by , we conclude that .
Now calculate:
.
This should equal the sum from to minus the missing number.
The sum from to is ,
so the missing number is:
.
Mr. Wang wrote a sequence of consecutive natural numbers starting from on the blackboard: . Then he erased three numbers, two of which were prime numbers. If the average of the remaining numbers is , what is the maximum possible sum of the two prime numbers that were erased?
- A.
- B.
- C.
- D.
- E.
The average of these numbers is:
So the average is around 20, which suggests that is around 40.
Since 3 numbers were erased, the number of remaining numbers should be a multiple of 9.
Therefore, .
The sum of numbers from 1 to 39 is:
After erasing 3 numbers, 36 remain. The total sum of the remaining numbers is:
So the sum of the 3 erased numbers is:
Among the prime numbers less than 39, the maximum possible sum of two primes that add up to no more than 64 is: .
In a math competition, the top students received awards. Originally, there were first prize winners, second prize winners, and third prize winners. After an adjustment, the numbers changed to first prize winners, second prize winners, and third prize winners.
After the adjustment:
The average score of first prize winners decreased by points,
The average score of second prize winners decreased by points,
The average score of third prize winners decreased by point.
If the original average score of second prize winners was points higher than that of third prize winners, how many points higher is the adjusted average score of first prize winners compared to that of second prize winners?
- A.
- B.
- C.
- D.
- E.
Let the adjusted average scores of the first, second, and third prize winners be , , and , respectively.
According to the problem:
Simplifying:
Therefore:
Answer: After the adjustment, the average score of the first prize winners is points higher than that of the second prize winners.
Place and Place were apart. Calvin and Yvonne departed from the two places respectively and travelled towards each other. Calvin started his journey minutes later than Yvonne, but he travelled faster than Yvonne by . The two of them came across each other two hours after Calvin's departure from Place . Calvin travelled at( ).
- A.
- B.
- C.
- D.
- E.
Let travel at km per hour, and travel at km per hour.
Solving gives: .
travels at km per hour.
The ratio of the speed of train to that of train was . Train departed first and travelled from station to station When it was away from station , train left station for station . The two trains met each other at point . The ratio of the distance between point and station to that between point and station was . The distance between station and station was ( ) .
- A.
- B.
- C.
- D.
- E.
Let be the time taken by from departure until meeting .
Let ’s speed be , and ’s speed be .
When and meet, the ratio of the distances they have traveled is , which simplifies to .
Here, is the time from ’s departure to the meeting.
Let the distance between and be .
Then .
Andy was training on a circular track meters long. After completing the first lap, he felt that his performance was not ideal. So he increased his speed by , and as a result, he finished the lap seconds faster than in the first lap. How many seconds did it take him to run the first lap?
- A.
- B.
- C.
- D.
- E.
Let be the time Andy took to run the first lap.
From the problem, Andy’s speed for the first lap is:
Increasing his speed by for the second lap, the speed becomes:
Thus, the time taken for the second lap is:
Since the second lap is seconds faster than the first lap:
which gives seconds.
Therefore, Andy took seconds to run the first lap.
The distance between and is km. Two people, and , set out at the same time from to on bicycles. Person rides km per day, while person rides km per day but rests every other day. At the end of the day, the distance from for person is twice the distance from for person .
- A.
- B.
- C.
- D.
- E.
Casework:
(1) If the number of days is even, then for it is equivalent to riding $$
50 \text{km per day}.$$
Let be the number of days such that at the end of day , B’s distance from is twice ’s distance from .
We have the equation: which gives not a valid solution.
(2) If the number of days is odd, then except for the last day (when rides km), rides km per day on the previous days.
Let be the number of days such that at the end of day , ’s distance from is twice ’s distance from .
We have the equation which gives a valid solution.
Thus, at the end of the 15th day, ’s distance from is twice ’s distance from .
On a circular track, flags are placed at equal intervals. Person and person start at the same time from the same flag, running in the same direction. When they both return to the starting point together again, has run laps and has run laps. Excluding the starting flag position, how many times does overtake exactly at a flag position?
- A.
- B.
- C.
- D.
- E.
Let the distance between two adjacent flags be , so the circumference of the track is .
Since , let and .
For to overtake , must run more laps than .
Then:
Thus, the time taken for to overtake is:
In this time, covers a distance of:
For to overtake exactly at a flag position, the distance covered must be an integer, which requires to be even.
Thus: (the maximum is extra laps).
However, when , both runners return to the starting point.
Therefore, overtakes exactly at a flag position times.
After its speed was increased, a certain train departed from City at and arrived punctually at City at the next day. Its travel time was hours shorter than before the speed increase, and its average speed was faster than before. What is the distance between the two cities (in )?
- A.
- B.
- C.
- D.
- E.
Let the train’s speed before the increase be km/h, and the distance between the two cities be .
From the problem, the following equations can be set up:
It is easy to solve and obtain , .
Person starts walking from to , and minutes later, Person starts walking from to . Person walks 30 meters per minute faster than Person .They meet at point along the way. The time taken by Person to travel from to is minutes longer than from to . The time taken by Person to travel from to is minutes longer than from to . What is the distance between and in meters?
- A.
- B.
- C.
- D.
- E.
Let A walk meters per minute, then B’s speed is meters per minute.
Let minutes be the time B takes to walk from to .
From the problem, we have:
Solving the system gives:
Verification shows , satisfy the original equations.
Therefore, , .
The time A spends from to is minutes, and the distance is:
The research vessel Xuelong carried out a scientific expedition to Antarctica. Departing from Shanghai at its maximum speed of knots ( knot = nautical mile per hour), it would take more than days to reach Antarctica. This time, the vessel departed from Shanghai at a speed of knots and, after a certain number of days, successfully arrived at its destination. It then worked in the polar region for a certain number of days before returning at a speed of knots. On the rd day after leaving Shanghai, due to weather conditions, its sailing speed dropped to knots. Two days later, it continued at a speed of knots for another days to return to Shanghai. How many days did the Xuelong work in Antarctica?
- A.
- B.
- C.
- D.
- E.
Let be the number of days the Xuelong took to travel from Shanghai to Antarctica, and be the number of days it worked in Antarctica.
Then:
Simplifying gives the indeterminate equation:
From this, we find:
When , ; when , .
Since traveling from Shanghai to Antarctica at the maximum speed of knots ( knot = nautical mile/hour) takes more than days, we have:
Therefore, fits the conditions of the problem.
An express train departs from City toward City , while a slow train departs from City toward City . Both trains depart at the same time and stop upon reaching their destinations. Let the travel time of the slow train be hours, and let the distance between the two trains be . The relationship between and is shown in the figure. If the two trains meet at a point that is away from the midpoint between and , then what is the distance between and ?
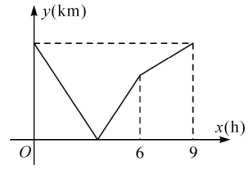
- A.
- B.
- C.
- D.
- E.
Let the speed of the express train be and the speed of the slow train be . Let the distance between City and City be . From the graph, we know that the express train takes hours to travel the entire distance, and the slow train takes hours. This gives the equation:
Since the two trains meet at a point away from the midpoint between and , we have:
By substituting into the equation:
Solving gives:
Therefore, the answer is .
A car and a truck depart from City toward City at the same time. After reaching City , the car immediately returns to City at a different speed, while the truck stops after reaching City . The graphs shown represent the relationship between the distance (in km) from City and the travel time (in hours) for the truck and the car, respectively. When the car is returning from City to City and meets the truck along the way, what is the distance from City to the meeting point?
- A.
- B.
- C.
- D.
- E.
From the problem, the speed of the car on its return trip to City is
Let the function representing the truck’s distance from City with respect to travel time be
Substituting the point gives:
so
Thus, the truck’s distance function is
Let the function representing the car’s distance from City on its return trip be
Substituting the points and gives:
Solving gives:
Thus, the car’s distance function on its return trip is
Solving the system
gives:
Therefore, when the car is returning from City to City and meets the truck, the meeting point is from City .
Teams , , and jointly undertake two projects, and . The workload of project is of the workload of project . If working alone, Teams , , and can complete project in , , and days respectively. At the beginning, Teams and work together on project , while Team works alone on project . After working for a certain number of days, the arrangement changes so that Team works alone on project , while Teams and work together on project . Both projects are completed at the same time. How many days did Team work on project ?
- A.
- B.
- C.
- D.
- E.
Method :
Let the total number of days be .
Solving gives .
Then the number of days Team worked on project is:
Method :
Let the workload of project be .
Then the work rates are: Team , Team , Team .
The workload of project is:
The total time for all three teams to complete both projects is:
The number of days Team worked on project is:
Liam is processing a batch of parts. If he makes parts per day, he will finish days later than originally planned. If he makes parts per day, he will finish days earlier than originally planned. How many parts are in this batch?
- A.
- B.
- C.
- D.
- E.
Let the originally planned production time be days, and let the total number of parts be .
Then:
From equation (),
Substituting into equation () gives:
Answer: The batch contains parts.
To build a water channel, Team can finish the job alone in days, and Team can finish it alone in days. If they work together, their efficiency decreases due to interference: Team ’s efficiency becomes of its original, and Team ’s efficiency becomes of its original. The plan is to complete the channel in days, with the goal of minimizing the number of days they work together. How many days should the two teams work together?
- A.
- B.
- C.
- D.
- E.
Team ’s individual work rate is , and Team ’s individual work rate is .
When working together, their combined work rate is:
To minimize the number of days they work together, the remaining work should be done by the faster Team .
Let be the number of days they work together.
Then:
Solving gives .
Therefore, the two teams need to work together for days.
Teams and are responsible for a project. At the normal rate of work, it would take days to complete. Now, Team ’s efficiency increases by one-half, and Team ’s efficiency decreases by one-half, and the project takes days to finish. How many days would it take Team alone to complete the project?
- A.
- B.
- C.
- D.
- E.
Let Team ’s work rate be and Team ’s work rate be .
We then have the system of equations:
Solving gives:
Thus, Team ’s work rate is , meaning Team alone would take days to complete the project.
A group of workers is assigned to load and unload a batch of goods, with each worker working at the same rate.
If all workers work together from the start, the job can be completed in hours.
Now, the method is changed: one worker starts alone, and then every hours (where is an integer) one more worker joins.
Each worker who joins continues working until the job is finished.
The last worker added works for a time equal to one quarter of the first worker’s total working time.
What is the maximum number of workers that can be used to complete the job?
- A.
- B.
- C.
- D.
- E.
Let the loading and unloading work take hours to complete.
The first worker works for hours, and the last worker works for hours.
Together, they work for hours, so the average time worked per person is hours.
From the problem statement, we know:
The second worker and the second-to-last worker, the third worker and the third-to-third-last worker, and so on, each also work an average of hours.
Therefore:
Solving gives:
With the new loading and unloading method, the total time is hours.
Let be the total number of workers.
Since one worker is added every hours, the last worker works hours less than the first worker.
From the problem, we have:
Since and are both positive integers:
Thus, the number of workers could be or .
Therefore, the maximum number of workers is .
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30

