2018 AMC 8

Complete problem set with solutions and individual problem pages

Problem 19 Hard

In a sign pyramid a cell gets a "+" if the two cells below it have the same sign, and it gets a "-" if the two cells below it have different signs. The diagram below illustrates a sign pyramid with four levels. How many possible ways are there to fill the four cells in the bottom row to produce a "+" at the top of the pyramid?

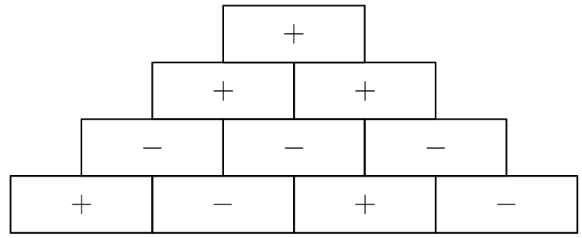
Answer:C

Solution 1

You could just make out all of the patterns that make the top positive. In this case, you would have the following patterns:

+−−+, −++−, −−−−, ++++, −+−+, +−+−, ++−−, −−++. There are 8 patterns and so the answer is .

Solution 2

The top box is fixed by the problem.

Choose the left 3 bottom-row boxes freely. There are ways.

Then the left 2 boxes on the row above are determined.

Then the left 1 box on the row above that is determined

Then the right 1 box on that row is determined.

Then the right 1 box on the row below is determined.

Then the right 1 box on the bottom row is determined, completing the diagram.

So the answer is .