AMC 8 Daily Practice - Triangle Properties

Complete problem set with solutions and individual problem pages

Problem 2 Easy

As shown in the figure, in triangle ABC, \angle ACB = 90^\circ, BC = 1, point D is the midpoint of side AB, and CD bisects the perimeter of triangle ABC. What is the length of BD?

  • A.

    \frac{\sqrt{2}}{4}

  • B.

    \frac{\sqrt{2}}{2}

  • C.

    1

  • D.

    \sqrt{2}

  • E.

    2

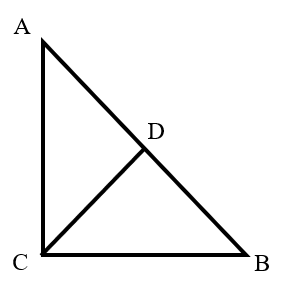
Answer:B

Since CD bisects the perimeter of triangle ABC, the perimeter of triangle ACD is equal to the perimeter of triangle BCD.

That is: AC + AD + CD = BC + BD + CD.

Simplifying, we get: AC + AD = BC + BD.

Since D is the midpoint of AB, AD = BD.

Substituting this into the equation above, we have: AC = BC

Given BC = 1, it follows that AC = 1.

In the right triangle ABC with \angle ACB = 90^\circ, by the Pythagorean theorem: AB = \sqrt{AC^2 + BC^2} = \sqrt{1^2 + 1^2} = \sqrt{2}.

Since D is the midpoint of AB, the length of BD is: BD = \frac{AB}{2} = \frac{\sqrt{2}}{2}.

Related Problems
Problem 1 AMC 8 Daily Practice - Triangle Properties
Problem 3 AMC 8 Daily Practice - Triangle Properties
Problem 4 AMC 8 Daily Practice - Triangle Properties
Problem 5 AMC 8 Daily Practice - Triangle Properties
Think Academy Powered by ChatGPT