AMC 8 Daily Practice - Area Tricks

Complete problem set with solutions and individual problem pages

Problem 8 Medium

In rectangle ABCD, E and F are the midpoints of AD and CD respectively. Given that EF = 4 and FB = 6, what is the area of the rectangle?

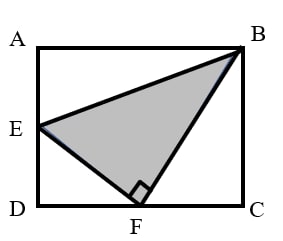
  • A.

    20

  • B.

    25

  • C.

    32

  • D.

    40

  • E.

    64

Answer:C

Draw EG through point E parallel to CD, and draw FH through point F parallel to AD.

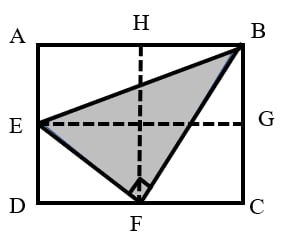
We observe that:

The area of \triangle ABE is \frac{1}{4} of the area of the rectangle.

The area of \triangle BCF is \frac{1}{4} of the area of the rectangle.

The area of \triangle DEF is \frac{1}{8} of the area of the rectangle.

Therefore, the area of \triangle EFB is \frac{3}{8} of the area of the rectangle.

The area of \triangle EFB is calculated as: \frac{4 \times 6}{2} = 12.

Let the area of the rectangle be A.

Then: \frac{3}{8}A = 12.

Solving for A: A = 12 \div \frac{3}{8} = 32.

Thus, the area of the rectangle is 32.

Related Problems
Problem 4 AMC 8 Daily Practice - Area Tricks
Problem 5 AMC 8 Daily Practice - Area Tricks
Problem 6 AMC 8 Daily Practice - Area Tricks
Problem 7 AMC 8 Daily Practice - Area Tricks
Think Academy Powered by ChatGPT