2021 AMC 10 B Fall

Complete problem set with solutions and individual problem pages

Problem 11 Medium

A regular hexagon of side length 1 is inscribed in a circle. Each minor arc of the circle determined by a side of the hexagon is reflected over that side. What is the area of the region bounded by these 6 reflected arcs?(2021 AMC Fall 10B, Question #11)

  • A.

    \frac{5 \sqrt{3}}{2}-\pi

  • B.

    3 \sqrt{3}-\pi

  • C.

    4 \sqrt{3}-\frac{3 \pi}{2}

  • D.

    \pi-\frac{\sqrt{3}}{2}

  • E.

    \frac{\pi+\sqrt{3}}{2}

Answer:B

Solution 1:

This is the graph of the original Hexagon. After reflecting each minor arc over the sides of the hexagon it will look like this;

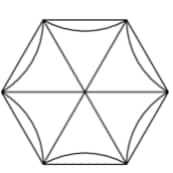
This bounded region is the same as the area of the hexagon minus the area of each of the reflect arcs. From the first diagram, the area of each arc is the area of the 60^{\circ} sector minus the area of the equilateral triangle, so each arc has an area of \frac{\pi r^{2}}{6}-\frac{s^{2} \sqrt{3}}{4} \Longrightarrow \frac{\pi}{6}-\frac{\sqrt{3}}{4}. There are 6 total arcs, so the total area of the arcs is 6 \cdot\left(\frac{\pi}{6}-\frac{\sqrt{3}}{4}\right)=\pi-\frac{3 \sqrt{3}}{2}. The area of the hexagon is 6 \cdot \frac{\sqrt{3}}{4}=\frac{3 \sqrt{3}}{2}, so the area of the bounded region is: \frac{3 \sqrt{3}}{2}-\left(\pi-\frac{3 \sqrt{3}}{2}\right)=3 \sqrt{3}-\pi=B

Solution 2:

Let the hexagon described be of area H and let the circle's area be C. Let the area we want to aim for be A. Thus, we have that C-H=H-A, or A=2 H-C. By some formulas, C=\pi r^{2}=\pi and H=6 \cdot \frac{1}{2} \cdot 1 \cdot\left(\frac{1}{2} \cdot \sqrt{3}\right)=\frac{3 \sqrt{3}}{2}. Thus, A=3 \sqrt{3}-\pi or (\text{B}).

Related Problems
Problem 9 2021 AMC 10 B Fall
Problem 10 2021 AMC 10 B Fall
Problem 12 2021 AMC 10 B Fall
Problem 13 2021 AMC 10 B Fall
Think Academy Powered by ChatGPT