AMC 8 Daily Practice - Circles
Complete problem set with solutions and individual problem pages
Problem 5 Easy
Given that the side length of square is and the side length of square is , and square has an inscribed circle , find the area of the circle.
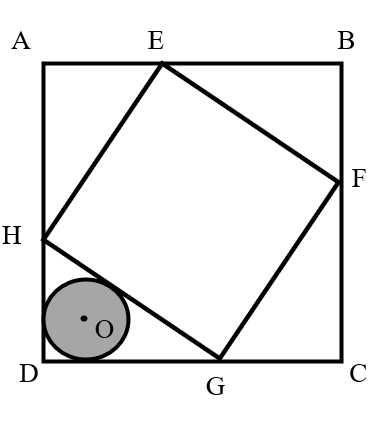
- A.
- B.
- C.
- D.
- E.
Answer:A
It is known that the four right triangles are congruent.
The area of one such right triangle is:
Let the radius of circle be .
Since circle is the inscribed circle (incircle) of the right triangle, connecting the three vertices of the triangle to the center divides the triangle into three smaller triangles, each with a height equal to .
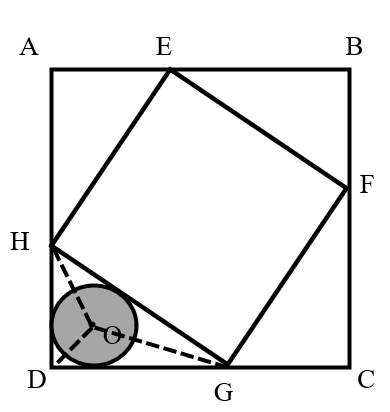
Factoring out , we get:
Notice that is equal to the sum of the side length of the large square and the side length of the small square, .
Substituting this in:
Thus, the area of circle is:
Answer: The area of the circle is square units.
