AMC 10 Daily Practice Round 3

Complete problem set with solutions and individual problem pages

Problem 14 Medium

A network of pathways lead from a single opening to three bins, labelled A, B, C as shown. If a ball is dropped into the opening, it will follow a path and land in one of the bins. Every time a path splits, it is equally likely for the ball to follow either of the downward paths. Ellen drops two balls, one after the other, into the opening. What is the probability that the two balls land in different bins?

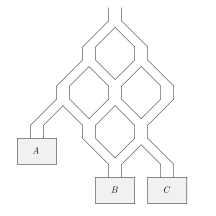
  • A.

    \frac { 1 7 } { 3 2 }

  • B.

    \frac { 2 7 } { 5 0 }

  • C.

    \frac { 2 5 } { 6 4 }

  • D.

    \frac { 1 } { 3 }

  • E.

    \frac { 1 5 } { 3 2 }

Answer:A

There are 6 different locations at which the path splits, and we label these splits 1 to 6, as shown.

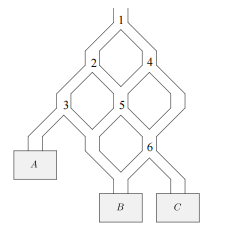
We begin by determining the probability that a ball lands in the bin labelled A.

There is exactly one path that leads to bin A.

This path travels downward to the left at each of the three splits labelled 1, 2 and 3.

At each of these splits, the probability that a ball travels to the left is \frac{1}{2}, and so the probability that a ball lands in bin A is \frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}=\frac{1}{8}.

Next, we determine the probability that a ball lands in the bin labelled C.

There are exactly three paths that lead to bin C.

One of these paths travels downward to the right at each of the three splits labelled 1, 4 and 6.

Thus, the probability that a ball lands in bin C by following this path is \frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}=\frac{1}{8}.

A second path to bin C travels downward to the right at split 1, to the left at split 4, to the right at split 5, and to the right at split 6.

The probability that a ball follows this path is \frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}=\frac{1}{16}.

The third and final path to bin C travels left at split 1, and to the right at each of the three splits 2, 5 and 6.

The probability that a ball follows this path is also \frac{1}{16}.

The probability that a ball lands in bin C is the sum of the probabilities of travelling each of these three paths or

\frac{1}{8}+\frac{1}{16}+\frac{1}{16}=\frac{2 + 1+1}{16}=\frac{4}{16}=\frac{1}{4}

Finally, we determine the probability that a ball lands in bin B.

There are six different paths that lead to bin B, and we could determine the probability that a ball follows each of these just as we did for bins A and C.

However, it is more efficient to recognize that a ball must land in one of the three bins, and thus the probability that it lands in bin B is 1 minus the probability that it lands in bin A minus the probability that it lands in bin C, or

1-\frac{1}{8}-\frac{1}{4}=\frac{8 - 1-2}{8}=\frac{5}{8}

The probability that the two balls land in different bins is equal to 1 minus the probability that the two balls land in the same bin.

The probability that a ball lands in bin A is \frac{1}{8}, and so the probability that two balls land in bin A is \frac{1}{8}\times\frac{1}{8}=\frac{1}{64}.

The probability that a ball lands in bin C is \frac{1}{4}, and so the probability that two balls land in bin C is \frac{1}{4}\times\frac{1}{4}=\frac{1}{16}.

The probability that a ball lands in bin B is \frac{5}{8}, and so the probability that two balls land in bin B is \frac{5}{8}\times\frac{5}{8}=\frac{25}{64}.

Therefore, the probability that the two balls land in different bins is equal to

1-\frac{1}{64}-\frac{1}{16}-\frac{25}{64}=\frac{64 - 1-4 - 25}{64}=\frac{34}{64}=\frac{17}{32}

Related Problems
Problem 12 AMC 10 Daily Practice Round 3
Problem 13 AMC 10 Daily Practice Round 3
Problem 15 AMC 10 Daily Practice Round 3
Problem 16 AMC 10 Daily Practice Round 3
Think Academy Powered by ChatGPT