2018 AMC 8
Complete problem set with solutions and individual problem pages
Problem 24 Hard
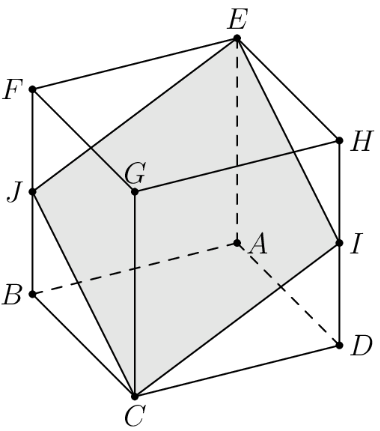
In the cube with opposite vertices and and are the midpoints of segments and respectively. Let be the ratio of the area of the cross-section to the area of one of the faces of the cube. What is
- A.
- B.
- C.
- D.
- E.
Answer:C
Solution 1
Note that is a rhombus by symmetry. Let the side length of the cube be . By the Pythagorean theorem, and . Since the area of a rhombus is half the product of its diagonals, the area of the cross section is . This gives . Thus, .
Solution 2
If the edges of the cube have same lengths , is the origin, is the positive direction, is the positive direction, and is the positive direction. Therefore, we have and . Hence, we can figure out that:
Note that is a rhombus, so . Finally, we can see that the answer is
