2020 AMC 10 B
Complete problem set with solutions and individual problem pages
As shown in the figure below, six semicircles lie in the interior of a regular hexagon with side length so that the diameters of the semicircles coincide with the sides of the hexagon. What is the area of the shaded region - inside the hexagon but outside all of the semicircles?(2020 AMC 10B, Question #14)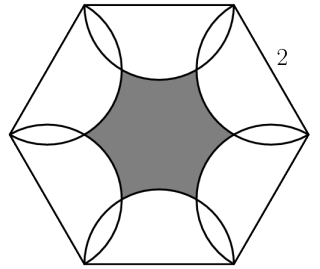
- A.
- B.
- C.
- D.
- E.
Solution 1:
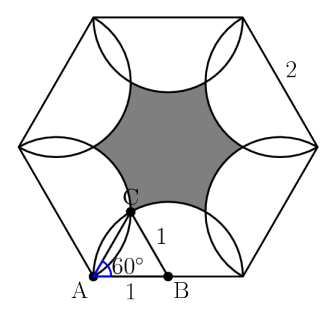 Let point be a vertex of the regular hexagon, let point be the midpoint of the line connecting point and a neighboring vertex, and let point be the second intersection of the two semicircles that pass through point . Then, , since is the center of the semicircle with radius 1 that lies on, , since is the center of the semicircle with radius 1 that lies on, and , as a regular hexagon has angles of 120 , and is half of any angle in this hexagon. Now, using the sine law, , so . Since the angles in a triangle sum to is also . Therefore, is an equilateral triangle with side lengths of .
Let point be a vertex of the regular hexagon, let point be the midpoint of the line connecting point and a neighboring vertex, and let point be the second intersection of the two semicircles that pass through point . Then, , since is the center of the semicircle with radius 1 that lies on, , since is the center of the semicircle with radius 1 that lies on, and , as a regular hexagon has angles of 120 , and is half of any angle in this hexagon. Now, using the sine law, , so . Since the angles in a triangle sum to is also . Therefore, is an equilateral triangle with side lengths of .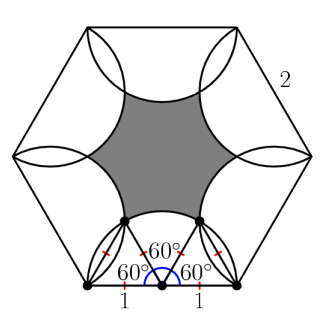 Since the area of a regular hexagon can be found with the formula , where is the side length of the hexagon, the area of this hexagon . is 2 . Since the area of an equilateral triangle can be found with the formula , where is the side length of the equilateral triangle, the area of an equilateral triangle with side lengths of 1 is . Since the area of a circle can be found with the formula , the area of a sixth of a circle with radius 1 is . In each sixth of the hexagon, there of a circle with radius 1 is . In each sixth of the hexagon, there sixth of a circle with radius 1 colored white, with an area of . The rest of the sixth is colored gray. Therefore, the total area that is colored white in each sixth of the hexagon is , which equals , and the total area colored white is , which equals . Since the area colored gray equals the total area of the hexagon minus the area colored white, the area colored gray is , which equals (D)
Since the area of a regular hexagon can be found with the formula , where is the side length of the hexagon, the area of this hexagon . is 2 . Since the area of an equilateral triangle can be found with the formula , where is the side length of the equilateral triangle, the area of an equilateral triangle with side lengths of 1 is . Since the area of a circle can be found with the formula , the area of a sixth of a circle with radius 1 is . In each sixth of the hexagon, there of a circle with radius 1 is . In each sixth of the hexagon, there sixth of a circle with radius 1 colored white, with an area of . The rest of the sixth is colored gray. Therefore, the total area that is colored white in each sixth of the hexagon is , which equals , and the total area colored white is , which equals . Since the area colored gray equals the total area of the hexagon minus the area colored white, the area colored gray is , which equals (D)
Solution 2:
First, subdivide the hexagon into 24 equilateral triangles with side length
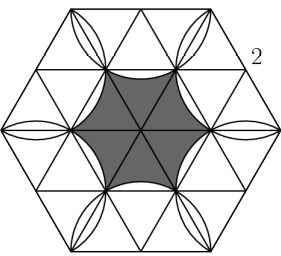
Now note that the entire shaded region is just 6 times this part: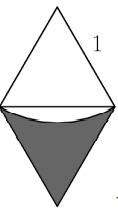
The entire rhombus is just 2 equilatrial triangles with side lengths of 1 , so it has an area of: Hence, the area of the shaded region in that section is For a final area
